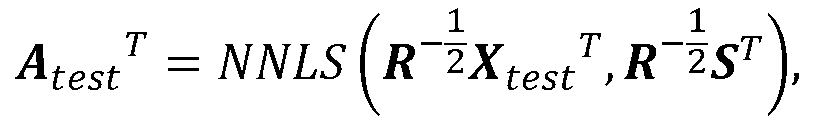JP7628731B2 - 検体に含まれる成分の含有量比の推定方法、組成推定装置、及び、プログラム - Google Patents

Description

本発明は、検体に含まれる成分の含有量比の推定方法、組成推定装置、及び、プログラムに関する。

従来、多成分の混合系である検体における成分組成を推定するための方法としては、例えば、検体中の各成分を何らかの方法で分離して、それぞれの分画成分を同定、定量する方法が知られている。この同定方法の一つとして、質量分析装置によって得られるマススペクトルが使われることがあった。

ところが、マススペクトルから得られる情報は、多数の相関関係を有する膨大な多次元データであるため、成分の同定につながる特徴的な信号を直感的、又は、経験的に抽出するのは困難であった。近年、非特許文献１に記載されているとおり、これらの多次元データを主成分分析によって次元削減し、特徴を探索する方法が用いられてきている。しかし、これら既知のデータ解析手法を用いても、ピーク強度がイオン化効率によって左右されるマススペクトルを用いて定量を行うことは本質的に困難であった。定量分析を行うためには、各化合物ごと有する未知変数であるイオン化効率をまず求める必要があり、そのためには検体量が既知、かつイオン化効率が同じとなる同位体検体を標準物質として用いる必要があった。

Ａｎａｌｙｔｉｃａｌ ｃｈｅｍｉｓｔｒｙ，２０２０，ｖｏｌ．９２，ｉｓｓｕｅ２，Ｐ．１９２５－１９３３

非特許文献１に記載された方法は、次元削減の過程で、もとの多次元データが有する多くの情報が失われ、成分の定性的な分析はできても、定量分析を行うことはできなかった。

また、そもそも、成分の種類や試験環境等によって、成分ごとのイオン化効率が異なるという特性がある以上、得られるマススペクトルの大きさ（面積）の比は、混合物中における各成分の含有量の比を反映せず、これがマススペクトルによる定量分析の妨げの一つの要因となっていた。

近年、質量分析方法の一つとして、アンビエントな条件（大気圧の開放空間にある）にある試料を前処理なしで質量分析するアンビエント脱離イオン化法（ＡＤＩ）が広く用いられるようになってきている。この方法は、未処理の試料や開放系の試料を固体のまま分析できるという利点がある一方で、各成分のイオン化率の不一致、及び、測定環境からの影響等によって、定量分析がより困難だと考えられてきた。

上記事情を考慮し、本発明はアンビエントな条件で得られるマススペクトルからであっても、未知の混合物の成分の組成を推定することができる、成分の含有量比の推定方法を提供することを課題とする。
また、本発明は、組成推定装置、及び、プログラムを提供することも課題とする。

本発明者らは、上記課題を達成すべく鋭意検討した結果、以下の構成により上記課題を達成することができることを見出した。

［１］ Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の上記成分を含む推定対象検体における、上記成分の含有量比を推定する方法であって、上記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、及び、上記成分を含まないバックグラウンド検体を準備することと、上記推定対象検体、上記学習用検体、及び、バックグラウンド検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測することと、加熱温度ごとに得られた上記マススペクトルを各行に格納し、上記検体ごとの二次元マススペクトルを得て、上記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換することと、上記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行うことと、上記基底スペクトル行列と上記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、上記ノイズ成分の影響を減ずるよう上記強度分布行列を補正して、補正後強度分布行列を得ることと、上記補正後強度分布行列を上記検体のそれぞれに対応する小行列に分割し、上記小行列を特徴ベクトルとして、ベクトル空間内で上記検体のそれぞれを表現することと、上記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、上記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定することと、上記Ｋ個のエンドメンバーと、上記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、上記ユークリッド距離の比により、上記推定対象検体中の上記成分の含有量比を推定することと、を含み、上記Ｋが３以上の場合、上記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、上記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、上記学習用検体が上記エンドメンバーの少なくとも１つを含む、方法。
［２］ 上記Ｋが２以上の整数であり、上記推定対象検体が、上記成分の混合物である、［１］に記載の方法。
［３］ 上記学習用検体が、上記エンドメンバーを含む、［１］又は［２］に記載の方法。
［４］ 上記エンドメンバーの決定が、上記学習用検体に付された判別ラベルに基づき行われる、［３］に記載の方法。
［５］ 上記エンドメンバーの決定が、上記学習用検体の上記特徴ベクトルの頂点成分分析によって行われる、［３］に記載の方法。
［６］ 上記エンドメンバーの決定が、上記Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムによって実施される、［１］に記載の方法。
［７］ 上記エンドメンバーの決定が、上記補正後強度分布行列を非負値行列因子分解し、上記検体中のＫ種類の上記成分の重量分率を表す行列と、Ｋ種類の個別の上記成分ごとのフラグメント存在強度を表す行列との積に分解する第２のＮＭＦ処理により行われる、［６］に記載の方法。
［８］ 上記学習用検体が、上記エンドメンバーを含まない、［６］又は［７］に記載の方法。
［９］ 上記補正後強度分布行列を得ることは、更に、上記強度分布行列の強度補正を行うことを含む、［１］～［８］のいずれかに記載の方法。
［１０］ 上記検体セットが、更に、キャリブレーション検体を含み、上記キャリブレーション検体は、上記Ｋ種類の成分を全て含み、かつ、その組成が既知であり、上記強度補正は、上記強度分布行列を規格化することを含む、［９］に記載の方法。
［１１］ 上記強度補正は、上記強度分布行列の少なくとも一部を、上記検体セットのうち対応する上記検体の質量と環境変数の積で割り付けることを含み、
上記環境変数は、上記観測の際における上記成分のイオン化効率への影響を表す変数である、［９］に記載の方法。
［１２］ 上記環境変数が、上記観測の際に、雰囲気中に所定量含まれる分子量５０～１５００の化合物、又は、上記検体セットのそれぞれに所定量含まれる分子量５０～５００の有機低分子化合物のマススペクトルのピークの合計値である、［１１］に記載の方法。
［１３］ Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の上記成分を含む推定対象検体における、上記成分の含有量比を推定する組成推定装置であって、上記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、上記成分を含まないバックグラウンド検体、及び、上記推定対象検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測する質量分析装置と、上記観測されたマススペクトルを処理する情報処理装置と、を備え、上記情報処理装置は、加熱温度ごとに得られた上記マススペクトルを各行に格納し、上記検体ごとの二次元マススペクトルを得て、上記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換する、データ行列作成部と、上記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行う、ＮＭＦ処理部と、上記基底スペクトル行列と上記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、上記ノイズ成分の影響を減ずるよう上記強度分布行列を補正して、補正後強度分布行列を作成する、補正処理部と、上記補正後強度分布行列を上記検体セットのそれぞれに対応する小行列に分割し、上記小行列を特徴ベクトルとして、ベクトル空間内で上記検体のそれぞれを表現する、ベクトル処理部と、上記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、上記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する、エンドメンバー決定部と、上記Ｋ個のエンドメンバーと、上記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、上記ユークリッド距離の比により、上記推定対象検体中の上記成分の含有量比を推定する、含有量比計算部と、を含み、上記Ｋが３以上の場合、上記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、上記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、上記学習用検体が上記エンドメンバーの少なくとも１つを含む、組成推定装置。
［１４］ 上記エンドメンバー決定部は、上記学習用検体に付された判別ラベルに基づいて上記エンドメンバーを決定する、［１３］に記載の組成推定装置。
［１５］ 上記エンドメンバー決定部は、上記Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムによって上記エンドメンバーを決定する、［１３］に記載の組成推定装置。
［１６］ 上記エンドメンバー決定部は、上記補正後強度分布行列を非負値行列因子分解し、上記検体中のＫ種類の上記成分の重量分率を表す行列と、Ｋ種類の個別の上記成分ごとのフラグメント存在強度を表す行列との積に分解する第２のＮＭＦ処理により上記エンドメンバーを決定する、［１５］に記載の組成推定装置。
［１７］ 上記補正処理部は更に、上記強度分布行列の強度補正を行う、［１５］に記載の組成推定装置。
［１８］ 上記検体セットが、更に、キャリブレーション検体を含み、上記キャリブレーション検体が、上記Ｋ種類の成分を全て含み、かつ、その組成が既知であり、上記強度補正が、上記強度分布行列を規格化することを含む、［１７］に記載の組成推定装置。
［１９］ 上記強度補正は、上記強度分布行列の少なくとも一部を、上記検体セットのうち対応する上記検体の質量と環境変数の積で割り付けることを含み、
上記環境変数は、上記観測の際における上記成分のイオン化効率への影響を表す変数である、［１７］に記載の組成推定装置。
［２０］ 上記質量分析装置は減圧ポンプを更に備え、上記環境変数が、上記減圧ポンプの稼働によって生ずる物質のマススペクトルのピークの合計値である、［１９］に記載の組成推定装置。
［２１］ Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の上記成分を含む推定対象検体における、上記成分の含有量比を推定する組成推定装置において用いられるプログラムであって、上記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、上記成分を含まないバックグラウンド検体、及び、上記推定対象検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測する質量分析装置と、上記観測されたマススペクトルを処理する情報処理装置と、を備え、上記質量分析装置によって、加熱温度ごとに取得された上記マススペクトルを各行に格納し、上記検体ごとの二次元マススペクトルを得て、上記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換する、データ行列作成機能と、上記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行う、ＮＭＦ処理機能と、上記基底スペクトル行列と上記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、上記ノイズ成分の影響を減ずるよう上記強度分布行列を補正して、補正後強度分布行列を作成する、補正処理機能と、上記補正後強度分布行列を上記検体のそれぞれに対応する小行列に分割し、上記小行列を特徴ベクトルとして、ベクトル空間内で上記検体のそれぞれを表現する、ベクトル処理機能と、上記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、上記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する、エンドメンバー決定機能と、上記Ｋ個のエンドメンバーと、上記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、上記ユークリッド距離の比により、上記推定対象検体中の上記成分の含有量比を推定する、含有量比計算機能と、を含み、上記Ｋが３以上の場合、上記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、上記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、上記学習用検体が上記エンドメンバーの少なくとも１つを含む、プログラム。

本発明の方法（以下「本方法」ともいう。）は、検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測し、得られた加熱温度ごとのマススペクトルを各行に格納した検体ごとの二次元マススペクトルを得て、これらをまとめたデータ行列を非負値行列因子分解（ＮＭＦ）によって、規格化された基底スペクトル行列とその強度分布行列の積に分解し、正準相関分析によって強度分布行列に含まれるノイズ成分を抽出して補正し、各検体の特徴ベクトルを含む補正後強度分布行列を得て、その後の定量計算を行う点に特徴点の一つがある。

この正準相関分析によって強度分布行列を補正する処理を行うことによって、（詳細は後述するが）より容易に、かつ、高精度で定量分析が可能になった。

また、Ｋが２以上の整数であり、推定対象となる検体（推定対象検体）がＫ種類の成分の混合物である場合、本方法によって、推定対象検体中におけるＫ種類の成分の混合比（組成）を推定することができる。

また、学習用検体がエンドメンバーを含む場合、より正確、かつ、より容易に検体の組成を推定することができる。

また、学習用検体にエンドメンバーの判別するための判別ラベルが付されている場合、そのラベルの情報からエンドメンバーを決定できるため、より容易に検体の組成を推定することができる。

また、判別ラベルが付されていない場合であって、学習用検体がエンドメンバーを含んでいる場合には、学習用検体の特徴ベクトルの頂点成分分析によってエンドメンバーを決定でき、検体の組成が推定できる。

また、学習用検体がエンドメンバーを含んでいない場合であっても、Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムを用いることによってエンドメンバーを決定することで、検体の組成が推定できる。学習用検体にエンドメンバーを必須としない点で優れている。

また、補正後強度分布行列が、強度分布行列の強度補正後のものであると、推定の正確性がより高まる。

また、検体セットが更に、キャリブレーション検体を含む場合であって、強度補正が強度分布行列を規格化することを含む場合、より簡便な手順で、より高精度に検体の組成が推定できる。

また、強度分布行列における各検体に対応する部分を検体の質量と環境変数の積で割り付けることによれば、観測の際における各成分のイオン化効率による影響が補正され、検体セットにキャリブレーション検体が含まれない場合であっても、検体の組成が高精度に推定できる。

また、上記割り付けに使用される環境変数が観測の際の雰囲気中に所定量含まれる分子量５０～１５００の化合物、又は、検体セットのそれぞれの検体に所定量含まれる分子量５０～５００の有機低分子化合物のマススペクトルのピークの合計値である場合、検体セットにキャリブレーション検体が含まれない場合であっても、より簡便な操作で、より正確な組成推定結果が得られる。

本発明の実施形態に係る組成推定方法のフローチャートである。 Ｋが３のときのＫ－１次元単体（２次元単体、三角形）を表すイメージ図である。 本発明の実施形態に係る組成推定装置のハードウェア構成図である。 本発明の実施形態に係る組成推定装置の機能ブロック図である。 「ＭＳＥ＿ｃａｌｉｂ」についてのオリジナルなスペクトル（Ａ）と、処理を行った後、再構築したスペクトル（Ｂ）を表す図である。 ＮＭＦ分解後のＣ行列の一部Ｃ_{δ（ＭＳＥ＿Ｃａｌｉｂ）}と、ＣＣＡ－Ｆｉｌｔｅｒによってバックグラウンド及び不純物のスペクトルを除いた後のＳ^Ｔである。 Ｍ（ポリメチルメタクリレート）、Ｓ（ポリスチレン）、Ｅ（ポリエチルメタクリレート）三成分系の組成解析結果である。 ＮＭＦの条件から、直交制約を解除した場合の組成推定結果である。 ＮＭＦ最適化の条件から、ｍｅｒｇｉｎｇ Ｓのみ解除した場合の組成推定結果である。 ＣＣＡ－ｆｉｌｔｅｒを解除した場合の結果（比較例）の組成推定結果である。 「ＭＳＥ＿ｃａｌｉｂ」についてのオリジナルなスペクトル（上、ｒａｗ ｏｆ ＭＳＥ＿ｃａｌｉｂ）と、ＣＣＡ－ｆｉｌｔｅｒを解除した上記で処理を行った後、再構築したスペクトルを表す図である。 環境変数による補正を行わなかった場合の組成推定結果である。 Ｋが３のときのＫ－１次元単体（２次元単体、三角形）を表すイメージ図である。 本発明の第２実施形態におけるエンドメンバーの決定方法の仕組みの説明図である。 実施例２の推定結果を表す図である。 実施例３の推定結果を表す図である。

以下、本発明について詳細に説明する。
以下に記載する構成要件の説明は、本発明の代表的な実施形態に基づいてなされることがあるが、本発明はそのような実施形態に制限されるものではない。
なお、本明細書において、「～」を用いて表される数値範囲は、「～」の前後に記載される数値を下限値及び上限値として含む範囲を意味する。

［用語の定義］
本明細書において使用される用語について説明する。なお、以下に説明のない用語については、当業者の間で普通に理解される意味で使用される。

本明細書において、「成分」とは、各検体を構成する物質を意味し、推定対象検体、学習用検体、及び、キャリブレーション検体は、成分の組合せによって構成される混合物を意味する。

「推定対象検体」とは、組成を推定すべき検体で、含まれている成分の数、及び、各成分の含有量はいずれも未知であってよい。

「学習用検体」とは、後述するＫ－１次元単体のＫ個のエンドメンバー決定に必要な検体を意味し、これらの検体には、Ｋ種類の成分から選択される少なくとも１種の成分が含まれ、それぞれ組成が異なっている。含まれる成分数は特に制限されず１～Ｋ種類であってよい。なお、学習用検体には、推定対象検体と同一の組成のものが含まれていてもよい。すなわち、推定対象検体と学習用検体とは同一であってもよいが、学習用検体はそれぞれ異なる。

「エンドメンバー」とは、Ｋ－１次元単体の頂点に対応するベクトルを意味し、このエンドメンバーは、Ｋ種類のうちの１成分のみからなる検体（学習用検体、又は、仮想の検体）の特徴ベクトルに対応する。

「バックグラウンド検体」とは、推定対象検体、及び、学習用検体とは異なる検体であって、上記成分のいずれをも含まない検体を意味する。

「キャリブレーション検体」とは、推定対象検体、学習用検体、及び、バックグラウンド検体とは異なる検体であって、Ｋ種類の成分を全て含み、その組成が明らかな検体を意味する。

［本方法の第１実施形態］
図１は、本発明の実施形態に係る組成推定方法（以下、「本方法」ともいう。）のフローチャートである。

まず、推定対象検体、互いに組成の異なるＫ個以上の学習用検体、及び、バックグラウンド検体（以上をまとめて「検体セット」という。）が準備される（ステップＳ１０１）。なお、検体セットは、キャリブレーション検体を更に含んでもよい。

推定対象検体は、Ｋ種類の成分のうち少なくとも１種の成分を含む。推定対象検体が１種類の成分を含む場合、本方法によってその成分の純度を推定することができる。この場合、推定対象検体には、上記「成分」と、それ以外の不純物とが含まれる。

Ｋが２以上の場合、推定対象検体は、成分の混合物である。本方法におけるＫは１以上であれば、上限は特に制限されない。典型的には、Ｋは、１０００以下が好ましい。
なお、学習用検体の個数は成分数Ｋに関係して、Ｋ個以上である必要がある。Ｋ個以上であれば、学習用検体の数としては特に制限されないが、より多い場合、後述するＫ－１次元単体の頂点の決定の精度がより高くなりやすく、結果として、より正確な組成推定結果が得られやすい。
すなわち、成分数Ｋに対する学習用検体の数の比（学習用検体の数／成分数）は、１以上であり、２以上が好ましく、３以上がより好ましく、５以上が更に好ましく、１０以上が特に好ましい。一方、上限値は特に制限されないが、一般に、１０００以下が好ましい。

学習用検体は、互いに組成が異なる。組成は、含まれる成分の種類と数、及び、各成分の含有量によって決まる。組成が同一とは、含まれる成分の種類、数、及び、それぞれの含有量が同一であることを意味し、いずれか１つが異なれば、それは「互いに組成が異なる」状態となる。

なお、本方法において、学習用検体は、互いに組成が異なっていれば、それ以外の情報、すなわち、含まれる成分の種類、成分数、及び、各含有量は、推定対象検体の組成推定には必要ない。すなわち、学習用検体の組成は、未知であってよい。
推定対象検体と学習用検体との相違点は、学習用検体はそれぞれ組成が異なることが必要である点である。なお、学習用検体は、推定対象検体と組成が同一のものを含んでいてもよい。

学習用検体は、エンドメンバーを含んでいてもよい。すなわち、学習用検体は、Ｋ種類の成分から選択される１種類の成分からなるもの（単味のもの、ピュア）を含んでもよい。学習用検体がエンドメンバーを含む場合、より容易に、高精度な組成推定が可能である。

このとき、エンドメンバーである学習用検体は、判別ラベルを含んでもよい。学習用検体が判別ラベルを含む場合、エンドメンバーの決定がより容易になる点で好ましい。

次に、推定対象検体をそれぞれ加熱して、熱脱着、及び／又は、熱分解によって生ずるガスを順次イオン化し、マススペクトルを取得する（ステップＳ１０２）。

マススペクトルを取得する方法としては特に制限されないが、アンビエントな条件にある試料を前処理なしで質量分析する方法が好ましい。このようなイオン化、及び、質量分析方法としては、ＤＡＲＴ（Ｄｉｒｅｃｔ Ａｎａｌｙｓｉｓ ｉｎ Ｒｅａｌ Ｔｉｍｅ）イオン源と呼ばれるイオン源と質量分析計とを組合わせたＤＡＲＴ－ＭＳと呼ばれる質量分析装置が知られている。
質量分析計としては特に制限されず、精密質量分析が可能なものが好ましく、四重極型、及び、飛行時間（ＴＯＦ）型等のいずれでもよい。

マススペクトルの取得について、具体的な条件は特に制限されないが、非限定的な一例を挙げると、検体セットに含まれるそれぞれの検体を順次５０℃／ｍｉｎの昇温速度で加熱し、５０～５５０℃の温度範囲で生じる熱分解ガスに対して５０ｓｈｏｔ／ｍｉｎの間隔でヘリウムイオンを噴射しガスをイオン化させ、横軸にｍ／ｚ、縦軸に温度を有する二次元ＭＳスペクトルを得るという手順が挙げられる。

次に、加熱温度ごとに得られたマススペクトルを各行に格納し、検体ごとの二次元マススペクトルを得て、この二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換する（ステップＳ１０３）。

データ行列の取得方法を具体的に説明する。

ステップＳ１０２では、所定の昇温間隔ごとに連続的にマススペクトルが取得される。これらのマススペクトルは、そのままデータ行列の作成に使用されてもよいが、所定の昇温温度範囲ごとに平均して使用されてもよい。所定の昇温温度範囲ごとに平均してマススペクトルを１本にまとめることで、データ量を圧縮することができる。このような昇温温度範囲としては、例えば、１０～３０℃程度が挙げられる。

また、各スペクトルにおいて、ピーク強度は規格化されていてもよい。規格化の方法としては、例えば、ピーク強度の二乗和が１になるように規格化する方法が挙げられる。

このようにすることで、ある検体について、一回の測定することで、加熱温度ごと（又は、所定の範囲ごとにまとめられた加熱温度ごと）に、所定の本数（まとめ方によって異なる、例えば、２０本等）のマススペクトルが得られる。
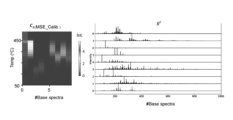
このマススペクトルが各行に格納され、加熱温度が各列に格納されると、検体ごとの二次元マススペクトルが得られる。

こうして、検体ごとの二次元マススペクトルが得られたら、これらの少なくとも２つ以上をまとめてデータ行列Ｘに変換する。
データ行列Ｘの作成に用いられる二次元マススペクトルの個数は２つ以上であれば特に制限されないが、検体セットに含まれる全検体の二次元マススペクトルが用いられることが好ましい。
なお、１つの検体について２回以上、測定が行われる場合には、２回以上の測定で得られた二次元マススペクトルの一部、又は、全てがデータ行列Ｘの作成に用いられてもよい。

次に、得られたデータ行列を非負値行列因子分解（ＮＭＦ）し、規格化された基底スペクトル行列と、その強度分布行列との積に分解する（ステップＳ１０４）。

非負値行列因子分解について説明する。

スペクトルの強度とサンプルの成分組成の間に線形加成性が成り立つという仮定の下で、スペクトルのデータ行列は一般に、

と行列分解できる。ここでデータ行列Ｘはチャンネル数ＭのスペクトルをＮ本積み重ねてできるＮ×Ｍのデータ行列、Ｓは基底スペクトル行列、Ｃはその強度分布行列である。データセットに含まれるすべての成分数をＫ_１とすればＣはＮ×Ｋ_１行列、ＳはＭ×Ｋ_１行列になる。実際の計測にはノイズが含まれるので、

と誤差行列Ｎを考慮にいれ、Ｎを最小化するようにＣ，Ｓ行列を定める。行列右肩のＴは転置行列を意味する。ここでガウスノイズを仮定すれば

なるＣ、Ｓについての最適化問題として定式される。なお、

は、行列のフロベニウスノルム、

は、ベクトルのＬ１ノルム、

は、ベクトルのＬ２ノルムを表すものとする。

なお、上式におけるＣ、Ｓは唯一解が定まらないので、物理的要請からスペクトルが満たすであろう拘束条件を課す。ＮＭＦは、組成比やスペクトル強度が非負の値をとるという自明な要請から、

として立式される。しかし、非負条件だけでは唯一解が定まらないので、測定装置に応じたさらなる拘束条件を適用することが求められる。以下では、本ステップにおけるＮＭＦの拘束条件について説明する。

（ＮＭＦ更新式について）
本ステップにおけるＮＭＦ処理は、以下に述べる制約を組み込みやすいＨｉｅｒａｒｃｈｉｃａｌ ａｌｔｅｒｎａｔｉｎｇ ｌｅａｓｔ ｓｑｕａｒｅ （ＨＡＬＳ）により、Ｃ、Ｓの列ベクトルワイズに交互に更新していくことで、上記式（数７）をＣ、Ｓの各列についての凸最適化問題として解くことが好ましい。

本方法では、各検体を加熱しながら、熱脱着、及び／又は、熱分解させて生じるガスについて質量分析を行うため、熱分解後の成分数Ｋ_１を事前情報として得ることは難しく、データから推定する必要がある。推定方法としては、Ａｕｔｏｍａｔｉｃ ｒｅｌｅｖａｎｃｅ ｄｅｔｅｒｍｉｎａｔｉｏｎ （ＡＲＤ）が好ましい。これは強度分布行列Ｃにスパース性を仮定するもので、ある成分の熱分解はその成分を含む検体の特定温度でのみ起こることを考えれば、自然な仮定といえる。これによりなるべく少ない成分数にする力と上記式（数７）を最小化する力が釣り合い、最適な成分数を求めることができる。

（直交制約）
質量分析計は、一般に０．１～０．００１ｍ／ｚ程度の分解能を有する。したがって、異なるガス成分のｍ／ｚが小数点以下まで一致し、同一のチャネルを占めるという状況は稀にしか生じない。したがって、基底スペクトル行列Ｓの列ベクトル間にはある程度の直交性を仮定するのが妥当である。

これには良い局所解に導く効果のみならず、強度の強いピークにのみフィッティングが集中することを防ぐ効果も期待できる。一方で、完全な直交かつ非負は強すぎる制約となってしまうので、ラグランジュ未定乗数を有するペナルティー項を加える形でソフトに直交制約を課すことが好ましい（ソフト直交制約）。

（成分のマージング）
ＣとＳの更新途中で、ほとんど同じ基底スペクトルが複数得られた場合は一つのスペクトルにまとめることで正しい成分数ｎを得ることができる。ＥＡＬＳのスペクトライメージをＮＭＦに適用すると、Ｓのｋ番目の列ベクトルをＳ_：ｋと書いて、Ｓ^Ｔ _：ｋＳ_：ｍ＞ｔｈｒｅｓｈｏｌｄなるｋ＜ｍが存在するときに、

によって一本化できる（Ｍｅｒｇｉｎｇ Ｃ）。ここでＴｈｒｅｓｈｏｌｄは０．９～０．９９で与えられるハイパーパラメータである。これと同様に類似Ｓのマージングを行い、更に、Ｃの複数の列ベクトルが平行であったときも、対応するＳの列ベクトルをＣの重みに応じて重ね合わせることが好ましい。すなわち、

なるｋ≠ｍが存在するときに、

と一本化する（Ｍｅｒｇｉｎｇ Ｓ）。これには同位体ピークやオリゴマーピークを一つの基底スペクトルにまとめる効果があると考えられる。

（更新式の立式）
上記によって得られる更新式について説明する。
モデルの全同時分布は

ここではσ^２は分散パラメータ、

の要素λ_ｋは成分ｋがデータ中に占める重要度を表す逆ガンマ分布に従うパラメータである。ノイズにガウス分布を仮定したので

Ｃが従う指数分布は、Ｋを初期値として入力する十分大きな任意の成分数（５０程度）として、

λ_ｋが従う逆ガンマ分布は、

ここでａはａ－１が極めて小さな正の数となるようなハイパーパラメータ、ｂはデータ行列の平均値μ_Ｘにより

として定まるパラメータである。また、Ｃの要素の期待値は

ｐ（Ｘ，Ｃ，Ｓ）の負の対数尤度は

ここで、ガウス分布を仮定したときの分散パラメータσ²は、

で与えられ、また、λについて凸関数なので

を得ることができる。
次に、Ｓの更新式について説明する。まず、負対数尤度関数からＳ_：ｋに関連する項Ｊ（Ｓ_：ｋ）のみを取り出すことを考える。Ｘに対するｋ成分の寄与、

を用いて、

と書けるので、定数項を除いて、

上記は、Ｓｈｉｇａ，Ｍ．ｅｔ ａｌ．Ｓｐａｒｓｅ ｍｏｄｅｌｉｎｇ ｏｆ ＥＥＬＳ ａｎｄ ＥＤＸ ｓｐｅｃｔｒａｌ ｉｍａｇｉｎｇ ｄａｔａ ｂｙ ｎｏｎｎｅｇａｔｉｖｅ ｍａｔｒｉｘ ｆａｃｔｏｒｉｚａｔｉｏｎ． Ｕｌｔｒａｍｉｃｒｏｓｃｏｐｙ １７０，４３－５９（２０１６）．をベースに導出された。ここで、上述したＳに加える直交制約によるペナルティー項を加える。

ここで、ξ_ｋはラグランジュ未定乗数、

である。ｓ_：ｋで微分して

とおいて、ｓ_：ｋについての更新式

を得る。完全直交条件を与えるξ_ｋは、

より、

より見積もることができる。ソフト直交条件はξ_ｋに［０，１］のハイパーパラメータｗをかけて、完全直交と直交制約なしとの間で自由に直交度合いを調整することができる。最終的な更新式は、

次に、Ｃの更新式について説明する。負対数尤度関数からＣ_：ｋに関連する項Ｊ（Ｃ_：ｋ）のみを取り出すことを考える。

と規格化しておけば、更新式は

より、

具体的なアルゴリズムは以下のとおりである。

図１に戻り、次に、基底スペクトル行列とデータ行列とを正準相関分析して補正後強度分布行列を得る（ステップＳ１０５）。
具体的には、基底スペクトル行列とデータ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、ノイズ成分の影響を減ずるよう強度分布行列を補正して、補正後強度分布行列を得る。

ＮＭＦはデータ行列の低ランク近似であるため、実際にはｉ番目のスペクトルには存在しない成分ｋであっても、存在するとしたほうが最小二乗の意味で近似が良くなるのであればＣ_ｉｋ＞０とする。多くの場合このようなＣ_ｉｋは非常に小さく、ＮＭＦ解析において問題にならない場合が多い。

しかし、微量成分検出においては、ｊ番目のスペクトルに微量実在するＣ_ｊｋ＞０と、ＮＭＦアーティファクトであるＣ_ｉｋ＞０を区別し、ゴーストピークであるＣ_ｉｋには０を代入することが好ましい。ＮＭＦアルゴリズムのアーティファクトに由来する偽ピークをノイズの１つとして除くことによりより精度の高い推定結果が得られるからである。

本ステップでは、上記を解決するために、正準相関分析（Ｃａｎｏｎｉｃａｌ Ｃｏｒｒｅｌａｔｉｏｎ Ａｎａｌｙｓｉｓ ）を用いる。本ステップは本方法の特徴点の一つであり、本発明者らは本ステップを、Ｃａｎｏｎｉｃａｌ Ｃｏｒｒｅｌａｔｉｏｎ Ａｎａｌｙｓｉｓ （ＣＣＡ） Ｆｉｌｔｅｒと命名した。

ＣＣＡ ｆｉｌｔｅｒは、概念的には、ＮＭＦから出力される基底スペクトルＳ^Ｔの各成分が実際に元データに含まれていたかをサンプルワイズにスキャンし、元データに類似のピークパターンが見られなければそのサンプルのスペクトルから消去することによる。Ｌ番目のサンプルから生成されるスペクトルがデータ行列Ｘのｌ行からｌ′行までに格納されていた場合、その部分を抜き出した小行列をＸ_δ（Ｌ)と書く。すなわちδ（Ｌ）＝｛ｌ，ｌ＋１，…，ｌ′－２，ｌ′－１｝ある。

ＣＣＡは従来、二系統のデータ間の相関を調べる手法として知られており、以下で定式される。
N個のｐ次元ベクトルからなる行列を

Ｎ個のｑ次元ベクトルデータからなる行列を

として、

ここで、

である。

すなわち、ある軸にＹとＺを投影して、その相関係数ρが最大となるような解（ａ^Ｔ，ｂ^Ｔ）^Ｔを見つけることがＣＣＡの問題設定である。

（ａ^Ｔ，ｂ^Ｔ）^Ｔと相関係数ρは次式の一般固有値問題の固有ベクトルと固有値として与えられ、すべての固有ベクトル（ａ^Ｔ，ｂ^Ｔ）^Ｔをまとめて（Ａ^Ｔ，Ｂ^Ｔ）^Ｔと書くと、

いま、ある成分ｋの基底スペクトルＳ_：ｋが、サンプルＬに含まれているか、いないかを判定したいとする。まず、データ行列Ｘから該当の部分データ行列Ｘ_δ（Ｌ）を抜き出す。一方Ｓ^Ｔは、Ｓ_：ｋ ^Ｔと似たすべてのスペクトル群をＳ_ｓｉｍ ^Ｔ、それとは大きく異なるスペクトル群をＳ_ｏｕｔ ^Ｔと、二つの行列に分け、

としてＣＣＡを行う。ここである値ｔ∈（０，１］に対して、ρ＞ｔ_１なるすべての固有値を取り出し、それに対応する固有ベクトルｂの第一成分がその最大成分に対してｂ_１＞ｔ_２ｂ_ｍａｘを満たせば、成分ｋの基底スペクトルＳ_：ｋがサンプルＬに含まれていると判定する。そうでなければ、対応するＣ_{δ（Ｌ）ｋ}＝０とする。
ここで、ｔ_１、ｔ_２はハイパーパラメータで、ＮＭＦのフィッティング精度、すなわちＮＭＦハイパーパラメータであるｔｈｒｅｓｈｏｌｄの影響を強く受けるので、慎重に吟味する必要がある。経験的にｔ_１＝０．９ｔｈｒｅｓｈｏｌｄ，ｔ_２∈［０．１，０．３］程度がよい結果を与える。

上記は、ＣＣＡ ｆｉｌｔｅｒをＮＭＦアーティファクト（ノイズ）に適用する例について説明したが、上記のノイズ除去は、ＮＭＦアーティファクトだけでなく、バックグラウンドやコンタミネーションの除去にも適用できる。

すなわち、ＣＣＡ ｆｉｌｔｅｒで除去できるノイズとしては、例えば、（１）ＮＭＦのアーティファクト（いわゆる偽ピーク）、（２）装置の周辺環境から紛れ込む微量化学物質由来のピーク（バックグラウンド）、（３）検体中に含まれるが、分析に含めるとその本質をゆがめる恐れのある物質由来のピーク（コンタミネーション）が挙げられる。

本方法で扱う検体セットには、バックグランド検体が含まれているため、

とすれば、基底スペクトルＳ_：ｋがバックグランドファイルに含まれていたどうかが判定できる。もし含まれていたのであれば、それは環境由来のシステムノイズであるから、Ｃ_：ｋ＝０とすればサンプルから当該スペクトルを取り除くことができる。

なお、更に、バックグラウンド検体がコンタミネーション物質を含む場合、上記と同様の手順によって、コンタミネーション由来のノイズも除去することができる。コンタミネーション物質としては特に制限されないが、例えば、検体の作製やロードに用いた溶媒等が挙げられる。

本ステップは更に、強度分布行列の強度補正を行うステップを含んでいてもよい。

例えば、ＤＡＲＴ－ＭＳは、空気中の水やアンモニアをヘリウムイオンで一次的にイオン化し、これによりサンプルを二次的にイオン化する。そのため、湿度等、大気条件によってピーク強度が変化する場合がある。またロードする検体質量も検体ごとに異なっているのが普通であり、これもピーク強度に影響を及ぼす。また、検体に含まれる各成分のイオン化効率も一般にはそれぞれ異なり、これもピーク強度に影響を及ぼす。
強度分布行列の強度補正によれば、上記の影響を減じて、より正確な定量結果を得ることができる。

全検体が、Ｋ種類の成分を全て含み、かつ、その組成が既知であるキャリブレーション検体を含む場合、上記強度補正は、上記強度分布行列を規格化することによって実施できる。

強度分布行列を規格化するとは、Ｃ行列を検体ごとに規格化することであり、より具体的には、検体ごとにすべての要素を足して１になるようにする操作を意味する。
Ｃ行列をサンプルワイズに分割し、サンプルＬに由来するＣ行列をＣ_δ（Ｌ）とかくと、

組成分析においては分解温度の情報は不要であるので、

を縦方向に加算して得られるベクトル

をサンプルＬの特徴量ベクトルとする。次にエンドメンバーとして測定したｐ個の単成分サンプルの特徴ベクトルを並べて、エンドメンバー行列

を作る。混合サンプルの特徴ベクトル

はエンドメンバーの特徴ベクトルの線形和で書けるので、その係数ベクトル

を使って、

と書ける。
一つのキャリブレーション検体は必ず一つ以上の熱分解サンプルを与えるので、熱分解後の成分数はＰは列フルランクな縦長の行列である。したがって一般的には解は不能で、最小二乗の意味での近似解は二次計画法で解くことができる。

本方法において得られるマススペクトルでは、イオン化効率が化合物ごとに異なるうえ、熱分解効率も異なり、化合物量とピーク強度は比例しない。
しかし、ＮＭＦによって成分ｋのイオン化効率を含めたピーク強度比はＳ_：ｋ ^Ｔの中にすでに反映されており、スペクトル間の強度比はＣ_：ｋに反映されている。
このＮＭＦによって形成された階層的データ構造のおかげで、エンドメンバーにおけるピーク強度比さえ考慮にいれれば、未知のイオン化効率を求めなくても、より正確な定量的な組成分析が可能になる。

一方、検体セットがキャリブレーション検体を含まない場合、強度分布行列の少なくとも一部（好ましくは全部）を、対応する検体の質量と環境変数の積で割り付けることによって、より正確な定量分析が可能となる。
ここで、環境変数とは、観測の際における各成分のイオン化効率への影響を表す変数である。

イオン化効率が高い成分であれば、ピーク強度は大きくなり、イオン化効率が低い成分であれば、ピーク強度が小さくなる。
また、検体の質量についても、これが大きくなれば、一般的にピーク強度は大きく成り、小さく成れば、ピーク強度は小さくなる。

検体セットがキャリブレーション検体を含まない場合、強度分布行列を規格化せず、強度分布行列が保持している検体間の強度情報を用いることができるよう、Ｃ行列を次のように補正する。

ここでｍ_ＬはサンプルＬの質量、Ｉ_Ｌは６１０ｍ／ｚに全温度域で観測される、ＤＡＲＴ－ＭＳ付属のオイルポンプから生じる（ポリ）ジメチルシロキサンのピーク強度である。Ｉ_Ｌはその測定時の待機状態を反映しており、実際雨の日と晴れの日ではピーク強度に３倍程度の差がある。これにより補正した

縦方向に加算して得られるベクトル

をサンプルＬの特徴ベクトルとする。あとは同様にエンドメンバーの特徴ベクトルからエンドメンバー行列

をつくり、

よりｒ_Ｌを求める。

なお、上記ではＩ_Ｌは、（ポリ）ジメチルシロキサン由来の６１０ｍ／ｚとしたが、上記に制限されず、観測の際に雰囲気中に所定量に含まれる分子量５０～１５００の化合物に由来するもの、及び／又は、全検体のそれぞれに所定量含まれる分子量５０～５００の有機低分子化合物に由来するものであることが好ましい。

図１に戻り、次に、補正後強度分布行列を検体セットに含まれる検体のそれぞれの検体に対応する小行列に分割し、これを特徴ベクトルとしてベクトル空間内で各検体を表現する（ステップＳ１０６）。
さらに、これらの特徴ベクトル（それぞれ各検体に対応する）の全てを内包するＫ－１次元単体を設定し、Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する（ステップＳ１０７）。

学習用検体がエンドメンバーを含む場合であって、学習用検体に判別ラベル（当該学習用検体が「エンドメンバー」であると判別するためのラベル）が付されている場合、そのラベルを元にエンドメンバーが決定される。

学習用検体がエンドメンバーを含む場合であって、学習用検体に判別ラベルが付されていない場合、すなわち、学習用検体にエンドメンバーが含まれてはいるが、どの学習用検体がエンドメンバーかが不明である場合、特徴ベクトルの頂点成分分析（Ｖｅｒｔｅｘ Ｃｏｍｐｏｎｅｎｔ Ａｎａｌｙｓｉｓ）によってエンドメンバーが決定される。

学習用検体がエンドメンバーを含まない場合には、Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムによってエンドメンバーが決定される。なお、Ｋ－１次元単体が最小体積になる、とは、２次元単体（３角形）の場合は、最小面積を意味する。

本方法の一形態においては、学習用検体がエンドメンバーを含まない場合でも、上記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、学習用検体の特徴ベクトルの少なくとも１つが位置しているため（Ｋが３以上の場合）、精度よくエンドメンバーを決定することができる。

図２は、Ｋが３のときのＫ－１次元単体（２次元単体、三角形）を表すイメージ図である。Ｋ－１次元単体１０は、学習用検体１６、１７、及び、１８によって決定されたエンドメンバー１３、１４、及び、１５を頂点とする三角形である。

図２のように、学習用検体１６、１７、及び、１８が、Ｋ－１次元単体の内接超球１２（この場合「円」）の外側の領域１９（ハッチング）のそれぞれに位置していると、精度の高い定量分析結果が得られる。
なお、上記はＲｏｂｕｓｔ Ｖｏｌｕｍｅ Ｍｉｎｉｍｉｚａｔｉｏｎ－Ｂａｓｅｄ Ｍａｔｒｉｘ Ｆａｃｔｏｒｉｚａｔｉｏｎ ｆｏｒ Ｒｅｍｏｔｅ Ｓｅｎｓｉｎｇ ａｎｄ Ｄｏｃｕｍｅｎｔ Ｃｌｕｓｔｅｒｉｎｇ， ＩＥＥＥ ＴＲＡＮＳＡＣＴＩＯＮＳ ＯＮ ＳＩＧＮＡＬ ＰＲＯＣＥＳＳＩＮＧ，ＶＯＬ． ６４，ＮＯ． ２３，ＤＥＣＥＭＢＥＲ １，２０１６をベースに考案された。

Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムとしては特に制限されず、公知のアルゴリズムが適用できる。このようなアルゴリズムとしては、例えば、Ｍｉｎｉｍｕｍ ｖｏｌｕｍｅ ｃｏｎｓｔｒａｉｎｔ－ＮＭＦ法、Ｍｉｎｉｍｕｍ Ｄｉｓｔａｎｃｅ Ｃｏｎｓｔｒａｉｎｔ－ＮＭＦ法、Ｓｉｍｐｌｅｘ ｉｄｅｎｔｉｆｉｃａｔｉｏｎ ｖｉａ ｓｐｌｉｔ ａｕｇｍｅｎｔｅｄ Ｌａｇｒａｎｇｉａｎ法、及び、Ｓｉｍｐｌｅｘ ｖｏｌｕｍｅ ｍｉｎｉｍｉｚａｔｉｏｎ法等が挙げられる。

次に、Ｋ個のエンドメンバーと、推定対象検体の特徴ベクトルとのユークリッド距離をそれぞれ計算し、検体中の各成分の含有量比を推定する（ステップＳ１０８）。

なお、本方法の他の一形態として、学習用検体が、エンドメンバーを少なくとも１つ含む（学習用検体の少なくとも１つがエンドメンバーである）場合、他の学習用検体の特徴ベクトルは、Ｋ－１次元単体に内接する超球体の内側の領域に位置していてもよい。図１３は、図２と同様に、Ｋが３のときのＫ－１次元単体（２次元単体、三角形）を表すイメージ図である。Ｋ－１次元単体６０は、エンドメンバーである学習用検体６１、それ以外の学習用検体６２、及び、学習用検体６３によって決定されたエンドメンバー６４、及び、６５を頂点とする三角形である。図２と異なるのは、学習用検体６２、及び、６３が、Ｋ－１次元単体に内接する超球体の内側の領域に位置していることである。

なお、学習用検体の少なくとも１つがエンドメンバーである場合であっても、他の学習用検体は、Ｋ－１次元単体に内接する超球体上に位置していてもよいし、外側の領域に位置していてもよい。すなわち、この場合、他の学習用検体の位置は任意でよい。
なかでも、より優れた本発明の効果が得られる点では、他の学習用検体は、エンドメンバーである学習用検体とは異なるエンドメンバーの成分（他のエンドメンバーの成分）を２０質量％以上含むことが好ましく、４０質量％以上含むことがより好ましい。

本方法によれば、溶媒に溶解しにくく、従来の組成分析が行いにくい固体の検体であっても、特段の前処理なしに分析に供することができ、かつ、正確な定量分析が可能になる。本方法は、特に、複数の成分の混合物である検体の品質管理、及び、不良原因の調査等に適用した場合、結果を得るために必要な時間を大幅に短縮することができる。

［本方法の第２実施形態］
本方法の第２実施形態は、すでに説明した第１実施形態におけるステップＳ１０７において、学習用検体がエンドメンバーを含まない場合、すなわち、Ｋ－１次元単体頂点に位置する学習用検体が１つもない場合のエンドメンバー（頂点）の決定方法を含む。

本実施形態に係る方法の特徴点の一つは、エンドメンバーの決定が、検体ごとのフラグメント存在強度を表す行列を非負値行列因子分解し、検体中のＫ種類の成分の重量分率を表す行列と、Ｋ種類の成分の各単体ごとのフラグメント存在強度を表す行列との積に分解する第２のＮＭＦ処理により行われる点にある。

図１４は、その仕組みを説明するための模式図である。
各検体は、Ｋ種類の成分の混合物（以下では、「ポリマー」の混合物として説明する）であるが、実際に観測できるのは、各ポリマーが熱分解して生じたＭ種類のフラグメントガスのスペクトルSの適当な線形和である。

本実施形態に係る上記特徴点は、その係数行列を

とすれば、

であり、仮にＫ個のポリマーの単体について測定できたとして、それが

と観測されたとすると、

と、二度目のＮＭＦ処理を行えば、組成Ｃが得られる、という着想に基づいている。

なお、ここで

はＫ個の単体（ポリマー）から生じるＭ個のフラグメントの存在量を表す。
以下では、図１のフローにおける、ステップＳ１０４のＮＭＦ処理（以下、「１回目のＮＭＦ処理」ともいう。）と、ステップＳ１０７におけるエンドメンバーの決定において実施されるＮＭＦ処理（以下「２回目のＮＭＦ処理」ともいう。）の違い等について詳述する。なお、以下に説明のないステップ等については、原則として、第１実施形態における各ステップと同様である。

以下の説明において、第１実施形態における説明で使用した各記号等を以下の表のとおり置き換えて説明する。

また、以下の説明において、多くは信号処理で一般的に使われている表記法に従う。

は、は非負、又は、実数のＮ×Ｍ行列を表す。
ある行列

に対して、

はそれぞれn番目の行ベクトル、m番目の列ベクトル、(n, m)-要素を表す。Ｘ^ＴはＸの転置行列、

はフロベニウスノルムを表す。

はＸのｎ行目の

を表す。Ｘが正方行列のとき、Ｔｒ（Ｘ）はトレース、ｄｉａｇ（Ｘ）は対角成分からなる対角行列を表す。１_Ｎと１１_Ｎはすべての要素が１のＮ次元ベクトル又は（Ｎ，Ｎ）行列を表す。Ｉ_ＮはＮ次元の単位行列を表す。

（１回目のＮＭＦ）

入力:データ行列

出力：分布行列

基底フラグメントスペクトル

ここで、Ｎ：サンプル数、Ｔ：温度帯域分割数、Ｄ：チャネル数、Ｍ：基底スペクトル数である。

一回目のＮＭＦは、志賀らによって提案されたＡＲＤ－ＳＯ－ＮＭＦに対して以下３点を主な変更点として加え、ＭＳ（Ｍａｓｓ ｓｐｅｃｔｒｏｍｅｔｒｙ）のデータ解釈によく適合するように開発した。

１）チャネルごとのガウスノイズの分散共分散行列

を自然同位体ピークに基づき見積もること

２）ソフト直交制約を基底フラグメントスペクトル間に適用すること

３）似た強度分布を有するフラグメントスペクトル同士を統合すること（マージング条件の拡張）

１）については、以下しばらくの間、分散σ^２で独立等分散（ｉ．ｉ．ｄ）のガウスノイズを仮定し、途中で分散共分散行列Ｒを導入する。ノイズにｉ．ｉ．ｄを仮定すると、データ行列Ｘの確率生成モデルは、

と書ける。基底スペクトル数Ｍは未知なので、自動的に推定できるように、ａｕｔｏｍａｔｉｃ ｒｅｌｅｖａｎｃｅ ｄｅｔｅｒｍｉｎａｔｉｏｎ （ＡＲＤ）を分布行列Ａのスパース性に基づいて導入する。まず、基底成分ごとにλ_ｍでパラメトライズされた指数分布をＡの事前分布として仮定する。

すなわち、

に対して、

全体の確率モデルとしては、

と書ける。ここで、ｐ（Ｓ）は、

の超球面上の一様分布を、ｐ（λ｜ａ，ｂ）は（ａ，ｂ）でパラメトライズされる逆ガンマ分布、すなわち

とする。ａはスパース性を調整するハイパーパラメータで、ａ＝１＋１０^－１６、ｂは経験的にＡ_ｉｍの期待値Ｅ（Ａ_ｉｍ）から見積もれて、

と関係づけられる。これは更にＥ（Ｘ_ｉｄ）と

なる関係があり、Ｅ（Ｘ_ｉｄ）をＸの平均μ_Ｘで近似すると、

よりｂは、

と定まる。したがって負対数尤度関数は、

と書ける。これはλに対して下に凸な関数なので、

すなわち、

としてλに関する更新式が得られる。ここまでは志賀らの報告したARD-SO-NMFの導出に完全に従った。

ノイズに対するｉ．ｉ．ｄガウス分布の仮定はＭＳデータについては当てはまらず、大きいシグナルほど大きなノイズを有する傾向があることが知られている。そこで、ノイズ分布

を自然同位体ピークによる線形回帰の残渣成分として求めた。すなわち、

ここで

はチャネルｄを中心にした［ｄ－３０，ｄ－２０，ｄ－１０，ｄ＋１０，ｄ＋２０，ｄ＋３０］なるチャネルで、チャネルｄの±３ｍ／ｚの同位体ピークである（チャネル間隔が０．１ｍ／ｚであることに留意）。チャネルごとの分散共分散行列

は

として求まる。これを用いて尤度関数を書き直すと、

となる。Rは定数行列であることに注意する。全体の負対数尤度関数は、

となる。λについての更新式Ｅｑ．Ｓ３を代入し、定数項を落として簡略化すると、

となる。この関数のＡ、Ｓに関する最小化はｈｉｅｒａｒｃｈｉｃａｌ ａｌｔｅｒｎａｔｉｎｇ ｌｅａｓｔ ｓｑｕａｒｅ （ＨＡＬＳ）により行う。簡便のため、以下のベクトル表記を用いる。

ＨＡＬＳでは残差Ｘ－ＡＳを

として表す。ここで

である。これによりＬ（Ｘ，Ａ，Ｓ，λ）は成分ｍごとに分離して書けて、

Ｓについてのソフト直交制約はペナルティー項

として目的関数Ｌに組み込むことができる。ここで

である。この項はｍ－成分とその他成分の非直交性を表し、ξ_ｍは厳密に直交性が満たされる際のラグランジェ未定乗数を表す。この項は更にｗ_Ｏ∈［０，１］によって緩和される。したがって最小化すべき目的関数は、

となり、ａ_ｍとｓ_ｍに関する勾配は、

となり、これらをゼロと置けば、更新式は

となる。ｓ_ｍは更新毎に規格化されるので、定数係数は省略した。非負制約は、更新毎に非負象限に射影することにより満たした。具体的には例えば、

によって射影できる。ここで

は要素ごとに絶対値を取ったベクトルを意味する。未定乗数ξ_ｍは

をＥｑ．Ｓ６の左側から乗じ、厳密な直交条件、

とｗ_Ｏ＝１を適用することで、

と得られる。以上Ｅｑ．Ｓ１－Ｓ７を用いて以下のアルゴリズム１を提案する。

ここで、ＡとＳの更新毎に、似た成分同士をマージングするようにする。同様のスペクトルを有する成分同士をマージすることが志賀らに提案されているが、ここではさらに、同様の強度分布を有する成分同士もマージングすることにした。これにより、同位体ピーク、異なるイオン付加によりイオン化されたフラグメントシリーズ、モノマー数違いのオリゴマーピークシリーズなどを一つの成分とすることで、より解釈性の高い結果を与えることができる。

（Ｃａｎｏｎｉｃａｌ ｃｏｒｒｅｌａｔｉｏｎ ａｎａｌｙｓｉｓ ｆｉｌｔｅｒ （ＣＣＡ－ｆｉｌｔｅｒ）の導出）

入力：１回目ＮＭＦの出力

、バックグラウンドスペクトル

出力：バックグランド由来と判定された成分番号のリスト

１回目のＮＭＦで得られたＭ－成分の中には、バックグランドや混入物に由来する成分が含まれ、これらは組成分析結果をゆがめる可能性があるため、ＡやＳから取り除くことが好ましい。Ｍ′－成分がバックグラウンド由来の成分だとＣＣＡ－ｆｉｌｔｅｒにより判定されたとすると、

及び

はそれぞれ、

と

になる。単純のため、ＣＣＡ－ｆｉｌｔｅｒ適用後の成分数はＭ－Ｍ′になるが、一貫してＭを用いる。
ＣＣＡ－ｆｉｌｔｅｒを用いるためには、バックグラウンドスペクトル

をデータセットに含めて、サンプルスペクトルと併せて１回目のＮＭＦを行う必要がある。もし何らかの混入物が予想できる場合は、その混入物について測定したスペクトルをＸ_ＢＧとして用いることができる。ＣＣＡ－ｆｉｌｔｅｒは成分ｍ＝１，…，Ｍについてひとつずつ、そのスペクトルＳ_ｍ：がＸ_ＢＧに含まれているか確認していく。
最初のステップは、Ｍ－スペクトルからなる

されたＳを、Ｓ_ｍ：に似たスペクトルセット

と、似ていないスペクトルセット

に分割することである。この分割は、

が満たされるように行う。ｔ_１∈［０，１］はある閾値で本発明では一貫してｔ_１＝０．２を用いた。なお、Ｓ_ｍ：は常にＹに含まれるので、Ｙの一列目にＳ_ｍ：を格納した。ＺはＸ_ＢＧと結合し、

とした。ＹとＺは、平均ゼロとなるように、

とした。これら二つのスペクトルセットに対して、ＣＣＡを行う。ＣＣＡは、二つのスペクトルセット内の線形結合により、なるべく似たペアのスペクトルを作り出す。

及び

の線形結合の係数がベクトル

及び

に格納されているとする。従ってスペクトルペアはそれぞれ、

及び

と書ける。その類似度は相関係数ρによって評価され、

ここで、

ＣＣＡの問題設定は、

と書ける。その解

は一般固有値問題の解として与えられて、

ここで

は固有ベクトル

をその固有値が大きい順に列ベクトルとして並べて得られる行列である。
各固有値

は、対応する（ｕ^＊，ｖ^＊）を係数として線形結合で作られたｙとｚの相関係数になっている。ここではρ＞ｔ_２を満たすすべての固有値に対応するｕ^＊を取り出し、もしＳ_ｍ：の係数に対応する１番目の要素がｕ^＊に大きく寄与する大きな成分であれば、すなわち

であれば、成分ｍはバックグラウンドに由来する成分と判定して、システムから除く。ここでｔ_２∈［０．９，０．９９］、ｔ_３∈［０，１］である。これを以下にアルゴリズム２としてまとめた。

バックグラウンド成分が特定されたあとは、対応するＡの列ベクトル、及びＳの行ベクトルを削除することで、システムから除いた。
ＣＣＡ－ｆｉｌｔｅｒから出力された、バックグラウンドに由来するＭ′－成分除去済みの

（以下、簡単のためＭ－Ｍ′をＭと置き換えて、

と表す）は、サンプル量及び内部標準ピークで割り付け強度を補正する。その後、サンプルｎに関するＡの小行列部分Ａ^（ｎ）を一次元ベクトル化した

をサンプルｎの特徴ベクトルとして二回目のＮＭＦの入力としてもよいが、組成分析においてはＭ－フラグメントの温度分布は不要な情報のため、サンプル毎にすべての温度帯域を足し合わせてサンプル毎のＭ－フラグメント存在強度（ｆｒａｇｍｅｎｔ ａｂｕｎｄａｎｃｅ； ＦＡ）を表す

を入力としてもよい。ここでは簡単のため

について二回目のＮＭＦを行うことにする。

以下のセクションでは、Ｎｏｎ－ｎｅｇａｔｉｖｅ ｌｅａｓｔ ｓｑｕａｒｅ （ＮＮＬＳ）によるフィッティングを頻繁に使う。この問題は、最適な非負係数

を用いて、定数行列

の列ベクトル線形結合により

を近似するもので、

により求められる。これを解くには、ａｌｔｅｒｎａｔｉｎｇ ｄｉｒｅｃｔｉｏｎ ｍｕｌｔｉｐｌｉｅｒ ｍｅｔｈｏｄｓ （ＡＤＭＭ）（１）を含む数多くの最適化手法が使えるが、ここではＦｕ． ｅｔ． ａｌ． （２）により開発されたＡＤＭＭ－ＮＮＬＳを用いてこの問題をとき、解を

と表記する。近似するベクトルセットＹ＝［ｙ_１，．．，ｙ_Ｌ］に対応する非負係数ベクトルｘ_ｌ ^＊（ｌ＝１，．．，Ｌ）は個別に計算できて、

または行列形式で、

と書くことにする。ここで

である。同様の問題で、係数ベクトルの総和が１になるような拘束条件付の問題はｆｕｌｌｙ ｃｏｎｓｔｒａｉｎｅｄ ｌｅａｓｔ ｓｑｕａｒｅ （ＦＣＬＳ）とよばれ、ＡＤＭＭを用いて同じく解くことができて、

または行列表記で、

と書くことにする。

（２回目のＮＭＦ）

入力：サンプル毎のＦＡを表す

、基底Ｍ－フラグメントごとのスペクトル

、ポリマー成分数K

出力：サンプル毎のポリマー重量分率

、単位重量Ｋ－基底ポリマーごとのＦＡ

２回目のＮＭＦ：

は、リーマン計量を用いてその近似残差

を評価する、すなわち、

ここで、

である。下三角行列

をコレスキー分解Ｇ＝ＬＬ^Ｔにより得れば、

と書ける。ここで

であり、

と行列分解することと等値である。

の行ベクトルで張られるシンプレックスの体積項を

の行ベクトル間の非直交性項を

として、α＞０とβ∈［０，１］を重みとすれば、

により

が求まる。ここで、Ｆｕらは（３）外れ値へのロバスト性を付与するために、

なる重み行列の導入を提案している。ここで、ｐ∈（０，２］、かつεは小さな正則化パラメータである。本発明では、一貫してｐ＝１．５かつε＝１０^－８とした。最適化問題は

となる。Ｃと

はｂｌｏｃｋ ｃｏｏｒｄｉｎａｔｅ ｄｅｓｃｅｎｔ （ＢＣＤ） 理論により交互に最適化する。今、ｔ回の最適化を行い、

を得たとする。なお、初期化には、ｖｅｒｔｅｘ ｃｏｍｐｏｎｅｎｔ ａｎａｌｙｓｉｓ （ＶＣＡ）（４）を用いて、

のＮ－行ベクトルの中からシンプレックスのＫ－頂点に近いＫ個の行ベクトルを選択し、これを

とした。

に基づくＣのアップデートは、

により単純に行える。そこでＣ^（ｔ）に基づく

から

へのアップデートについて考える。なお、

で、

は未定乗数である。また

ここで、

は小さな正則化パラメータで、一貫してτ＝１０^－８を用いた。ここで、

のＭａｊｏｒｉｚｅｒ関数を導入する。接線不等式より、一期前の

に基づいて、

が成立する。ここで

は

のＨ^（ｔ）における勾配で、

より、

ここで、

かつ、ｃｏｎｓｔは定数項である。したがって、

を

で置き換えて、すべてのペナルティー項を合わせて書くと、

ここで

従って

のアップデートは以下を解くことで得られる。

複雑な制約条件を整理するために、

なる制約をラグランジェ未定乗数

を用いて、目的関数に組み込み、ＡＤＭＭの枠組みでこの問題を解く。

ここで、

かつμはＡＤＭＭのハイパーパラメータである（ここでは一貫してμ＝１とした）。Ｚ′は一期前のＺを表し、

のときに目的関数はＺについて最大化された、

を与える。これを

について最適化すればよい。

をサイクリックに最適化し、アルゴリズムをAlgorithm3にまとめた。

目的関数

は

については拘束条件なしの二次関数の最適化なので、

より最小化される。また

はＮＮＬＳにより解けて、

と更新される。以上より元の問題Ｅｑ．Ｓ１１を解くための

の更新式が得られた。最後にＶ＝αＦ^（ｔ）＋βΛ^（ｔ）の更新について考える。Ｆ^（ｔ）については

と簡単に求まる。Λ^（ｔ）は厳密な直交条件、すなわち

と

を組み合わせて、

をＥｑ．Ｓ１９の右側からかけると、

と得られる。Ｅｑ．Ｓ１８とＥｑ．Ｓ２０より、

が与えられる。以上を用いて、問題Ｅｑ．Ｓ１１を解くためのアルゴリズムは以下のとおりである。

（ＳとＢの張る超平面へのテストデータの射影）
データセットからＳとＢを推定したのちに、ＳとＢの推定には用いなかったデータ（ここではテストデータと呼ぶ）

を、ＳとＢの張る超平面へ射影する方法について述べる。
まずＳ－超平面への射影により、

が得られる。すなわち、

温度帯域について総和をとり、

に変換したのちに、Ｂ－超平面への射影と規格化により、

が得られる。すなわち、

なお、データセットとハイパーパラメータは以下のとおりである。

また、引用文献は、以下のとおりである。

（組成推定装置）
次に、本発明の実施形態に係る組成推定装置について、図面を参照しながら説明する。図３は、本発明の実施形態に係る組成推定装置のハードウェア構成図である。

組成推定装置３０は、質量分析装置３１と、情報処理装置３３とを備え、質量分析装置３１は、減圧ポンプ３２を備えている。情報処理装置３３は、プロセッサ３４と、記憶デバイス３５と、表示デバイス３６と、入力デバイス３７とを有し、質量分析装置３１と情報処理装置３３とは相互にデータを送受信できるよう構成されている。

プロセッサ３４は、例えば、マイクロプロセッサ、プロセッサコア、マルチプロセッサ、ＡＳＩＣ（ａｐｐｌｉｃａｔｉｏｎ－ｓｐｅｃｉｆｉｃ ｉｎｔｅｇｒａｔｅｄ ｃｉｒｃｕｉｔ）、ＦＰＧＡ（ｆｉｅｌｄ ｐｒｏｇｒａｍｍａｂｌｅ ｇａｔｅ ａｒｒａｙ）、及び、ＧＰＧＰＵ（Ｇｅｎｅｒａｌ－ｐｕｒｐｏｓｅ ｃｏｍｐｕｔｉｎｇ ｏｎ ｇｒａｐｈｉｃｓ ｐｒｏｃｅｓｓｉｎｇ ｕｎｉｔｓ）等である。

記憶デバイス３５は、各種プログラム、及び、データを一時的に、及び／又は、非一時的に記憶する機能を有し、プロセッサ３４の作業エリアを提供する。
記憶デバイス３５は、例えば、ＲＯＭ（Ｒｅａｄ Ｏｎｌｙ Ｍｅｍｏｒｙ）、ＲＡＭ（Ｒａｎｄｏｍ Ａｃｃｅｓｓ Ｍｅｍｏｒｙ）、ＨＤＤ（Ｈａｒｄ Ｄｉｓｋ Ｄｒｉｖｅ）、フラッシュメモリ、及び、ＳＳＤ（Ｓｏｌｉｄ Ｓｔａｔｅ Ｄｒｉｖｅ）等である。

入力デバイス３７は、各種情報入力を受け付け、また、組成推定装置３０への指示の入力を受け付けることができる。入力デバイス３７は、キーボード、マウス、スキャナ、及び、タッチパネル等でよい。

表示デバイス３６は、組成推定装置３０のステータス、分析の進捗、及び、組成推定結果等を表示できる。表示デバイス３６は、液晶ディスプレイ、及び、有機ＥＬ（Ｅｌｅｃｔｒｏ Ｌｕｍｉｎｅｓｃｅｎｃｅ）ディスプレイ等でよい。
また、表示デバイス３６は、入力デバイス３７と一体として構成されていてもよい。この場合、表示デバイス３６がタッチパネルディスプレイであって、ＧＵＩ（Ｇｒａｐｈｉｃａｌ Ｕｓｅｒ Ｉｎｔｅｒｆａｃｅ）を提供する形態が挙げられる。

データバスにより相互にデータを通信可能なプロセッサ３４、記憶デバイス３５、入力デバイス３７、及び、表示デバイス３６を備える、情報処理装置３３は、典型的にはコンピュータである。

質量分析装置３１は、減圧ポンプ３２を備え、典型的には、ＤＡＲＴイオン源、検体加熱装置、及び、飛行時間型質量分析計を備える質量分析装置である。質量分析装置３１が備えるイオン源、及び、質量分析計は、いずれも非限定的な例であり、本組成推定装置が備える質量分析装置の構成は上記に限定されない。

図４は、本発明の実施形態に係る組成推定装置３０の機能ブロック図である。組成推定装置３０は、全検体の質量分析を行う質量分析部４１と、質量分析部４１によって得られたマススペクトルを処理する情報処理部４２とを有する。

質量分析部４１は、質量分析装置３１を含んで構成され、質量分析装置３１が後述する制御部４３に制御されて実現する機能である。
質量分析部４１は、ロードされた検体セット（検体、学習用検体、及び、バックグラウンド検体、図４中、符号ａ）について、加熱しながら熱脱着、及び／又は、熱分解されて生ずるガス成分をイオン化し、順次質量分析して、マススペクトルを出力する（図４中、符号ｃ）。
この際、質量分析装置３１の設置されている環境に起因した環境要因（図４中、符号ｂ、例えば、減圧ポンプ３２から生ずる（ポリ）ジメチルシロキサン）も同時に質量分析装置３１にロードされ、マススペクトルに影響を与える。

次に、情報処理装置３３を含んで構成される情報処理部４２の各部の機能について説明する。
制御部４３は、プロセッサ３４を含んで構成される。制御部４３は、各部を制御して、組成推定装置３０の各機能を実現する。

記憶部４４は、記憶デバイス３５を含んで構成される。記憶部４４には予め各部の制御のためのプログラムが記憶され、また、各部によって入出力されるデータの一時的、又は、非一時的な記憶領域を提供する。記憶部４４は、制御部４３によって制御され、データを読み出したり、書き込んだりすることができる。

入力部４５は入力デバイス３７を含んで構成される。また、出力部４６は、表示デバイス３６を含んで構成される。制御部４３がこれらを制御することで、組成推定装置３０の使用者からの入力を受け付けて、これを記憶部４４に記憶させたり、記憶部４４に記憶された情報を各部に送信したり、出力部４６を介して組成推定装置３０の使用者に対して表示したりできる。

データ行列作成部４７は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
データ行列作成部４７は、質量分析部４１によって加熱温度ごとに取得されたマススペクトル（図４中、符号ｃ）を各行に格納した二次元マススペクトルからデータ行列Ｘを作成し、後述するＮＭＦ処理部４８に渡す（図４中、符号ｄ）。なお、データ行列Ｘの詳細については、すでに説明したとおりである。

ＮＭＦ処理部４８は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
ＮＭＦ処理部４８は、データ行列作成部４７によって作成されたデータ行列Ｘ（図４中、符号ｄ）を非負値行列因子分解（ＮＭＦ）し、規格化された基底スペクトル行列（Ｓ）とその強度分布行列（Ｃ）との積（Ｘ＝Ｃ×Ｓ^Ｔ）に分解する。その結果は、補正処理部４９に渡される（図４中、符号ｅ）。なお、ＮＭＦ処理の詳細はすでに説明したとおりである。

補正処理部４９は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
補正処理部４９は、ＮＭＦ処理部４８によって作成された基底スペクトル行列とデータ行列との正準相関分析によって強度分布行列を補正して、補正後強度分布行列を作成する機能である。作成された補正後強度分布行列はベクトル処理部５０に渡される（図４中、符号ｆ）。

なお、補正処理部４９は、上記の正準相関分析による補正に加えて、すでに説明した強度補正を更に行ってもよい。この際、強度補正に用いるキャリブレーション検体の組成（ｃａｌｉｂ検体組成）がある場合は、入力部４５を介して補正処理部４９に渡される（図４中、符号ｋ）。正準相関分析による補正（ＣＣＡ ｆｉｌｔｅｒ）、及び、強度補正の詳細はすでに説明したとおりである。

ベクトル処理部５０は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
ベクトル処理部５０は、補正処理部４９により作成された補正後強度分布行列を全検体のそれぞれに対応する小行列に分割し、これを特徴ベクトルとしてベクトル空間内で全検体を表現する。この結果は、エンドメンバー決定部５１に渡される（図４中、符号ｇ）。

エンドメンバー決定部５１は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
エンドメンバー決定部５１は、ベクトル処理部５０によって作成された特徴ベクトルの全てを内包するＫ－１次元単体を設定し、Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する。この結果は、含有量比計算部５２に渡される（図４中、符号ｈ）。

この際、学習用検体にエンドメンバーが含まれる場合であって、判別ラベルを有する場合には、入力部４５から判別ラベルの情報がエンドメンバー決定部５１に渡される（図４中、符号ｊ）。
しかし、すでに説明したとおり、エンドメンバーの決定（エンドメンバー決定部５１の処理）には判別ラベルは必須ではない。

含有量比計算部５２は、記憶部４４に記憶されたプログラムが制御部４３により実行されて実現される機能である。
含有量比計算部５２は、エンドメンバー決定部５１によって決定されたＫ個のエンドメンバーと、ベクトル処理部５０により作成された推定対象検体の特徴ベクトルとのユークリッド距離をそれぞれ計算し、Ｋ個のエンドメンバーと検体の特徴ベクトルとのユークリッド距離の比から、推定対象検体中のＫ個の成分の含有量比を推定する。この含有量比の推定結果（図４中、符号ｉ）は、出力部４６から出力される。
なお、この際、学習用検体の組成推定結果もあわせて出力してもよい。

本組成推定装置よれば、溶媒に溶解しにくく、従来の組成分析が行いにくい固体の検体であっても、特段の前処理なしに分析に供することができ、かつ、正確な定量分析結果が得られる。本組成推定装置は、特に、複数の成分の混合物である検体の品質管理、及び、不良原因の調査等に適用した場合、結果を得るために必要な時間を大幅に短縮することができる。

以下では、実施例をもとに、本組成分析方法について詳述する。なお、本発明の組成分析方法は下記の特定の実施例によって限定的に解釈されるものでない。

［実施例１］
（検体の準備）
ポリメチルメタクリレート（ｐｏｌｙ（ｍｅｔｈｙｌ ｍｅｔｈａｃｒｙｌａｔｅ）、記号「Ｍ」）、ポリスチレン（ｐｏｌｙｓｔｙｒｅｎｅ、記号「Ｓ」）、ポリエチルメタクリレート（ｐｏｌｙ（ｅｔｈｙｌ ｍｅｔｈａｃｒｙｌａｔｅ）、記号「Ｅ」）の三種類の高分子のジオキサン溶液（約４質量％、高分子の固形分として０．４ｍｇ程度）を、サンプルポット上にキャストした後に一晩風乾して検体を得た。表４は、各検体の組成である。なお、質量分析は、ＳＨＩＭＡＤＺＵ社製ＬＣＭＳ－２０２０を検出器として、ＩｏｎＳｅｎｓｅ社製ＤＡＲＴイオン源として、バイオクロマト社製イオンロケットをサンプルの加熱部として用いて行った。

得られたマススペクトルについて、以下の（ｉ）～（ｉｖ）を実装したアルゴリズムによって解析を行った。

（ｉ）Ｃ行列ＡＲＤとＳ行列へのソフト直交制約
（ｉｉ）ＮＭＦ最適化中のマージング条件
（ｉｉｉ）ＣＣＡ－ｆｉｌｔｅｒによるＮＭＦアーティファクト、及び、バックグラウンド、コンタミネーション除去
（ｉｖ）環境変数を補正項にいれることで、キャリブレーション不要の定量分析

解析に使用したハイパーパラメータは以下のとおりである。
ＮＭＦ：
ｏｒｔｈｏｇｏｎａｌ ｃｏｎｓｔｒａｉｎ ｗｅｉｇｈｔ ｗ＝０．２， ｉｎｉｔｉａｌ ｃｏｍｐｏｎｅｎｔ ｎｕｍｂｅｒ Ｋ＝５０， ｓｍａｌｌ ｐｏｓｉｔｉｖｅ ｎｕｍｂｅｒ ａ＝１＋０．１^－１５， ｉｔｅｒａｔｉｏｎ ｎｕｍｂｅｒ Ｌ＝２０００， ｔｈｒｅｓｈｏｌｄ＝０．９
ＣＣＡ－Ｆｉｌｔｅｒ：
ｔ_１＝０．８，ｔ_２＝０．２，

図５は、「ＭＳＥ＿ｃａｌｉｂ」についてのオリジナルなスペクトル（Ａ）と、上記処理を行った後、再構築したスペクトル（Ｂ）を表す図である。両者の波形は類似していることがわかる。すなわち、上記処理によってオリジナルなスペクトルの特徴は保存され、組成分析に用いやすいデータとなったことが示された。

また、オリジナルデータにはエアコン等から排出されるフタル酸エステル等のバックグラウンドが３９０ｍ／ｚに観測される（図５（Ａ）中、「ＢＧ」と表示した部分）が、再構築されたピーク（Ｂ）では、これが除去されている。また、検体の作成に用いられた溶媒であるジオキサン（図５（Ａ）中、「ＤＯＸ」と表示した部分）も除去されていた。これらはいずれもノイズに該当するものであり、本方法によって、効果的にノイズが除去されたことが示された。

また、図６は、ＮＭＦ分解後のＣ行列の一部Ｃ_{δ（ＭＳＥ＿Ｃａｌｉｂ）}と、ＣＣＡ－Ｆｉｌｔｅｒによってバックグラウンド及び不純物のスペクトルを除いた後のＳ^Ｔである。

図７は、Ｍ、Ｓ、Ｅ三成分系の組成解析結果である。図７中、中空円で表され、凡例に「Ｃａｌｉｂｒａｔｅｄ」とあるのは、ＭＳＥ＿ｃａｌｉｂをキャリブレーション検体とした場合、つまり、ＭＳＥ＿ｃａｌｉｂの組成情報を既知として与え、強度分布行列を強度補正した場合の検体の組成推定結果である。

また、図７中、中実円で表され、凡例に「Ｎｏｎ－ｃａｌｉｂｒａｔｅｄ」とあるのは、環境変数（すなわち、６１０ｍ／ｚ：ポリジメチルシロキサンのピーク強度）と検体質量の積を用いて、強度分布行列を強度補正した場合の検体の組成推定結果である。

また、図７中、星印で表され、凡例に「Ｋｎｏｗｎ」とあるのは、実際の組成（真の値）を表している。

図７に示した結果から、「Ｃａｌｉｂｒａｔｅｄ」、「Ｎｏｎ－ｃａｌｉｂｒａｔｅｄ」のいずれの場合にも真の値に近い、優れた推定結果が得られた。

次に、図８は、ＮＭＦの条件から、（１）の直交制約を解除した場合の組成推定結果である。各プロットの定義は、図７と同様である。
図８の結果から、ＮＭＦが直交制約を有する方が、より優れた推定結果が得られることがわかった。

次に、図９は、ＮＭＦ最適化の条件から、ｍｅｒｇｉｎｇ Ｓのみ解除した場合の組成推定結果である。各プロットの定義は、図７と同様である。
図９の結果から、ＮＭＦ最適化の条件がｍｅｒｇｉｎｇ Ｓを有する方が、より優れた推定結果が得られることがわかった。
なお、成分数はＡＲＤによって３６までしか減らせないが、Ｍｅｒｇｉｎｇ Ｓの条件を維持したときは成分数９でより精度よく組成が推定できることから、Ｍｅｒｇｉｎｇ Ｓの重要性がわかった。

図１０は、ＣＣＡ－ｆｉｌｔｅｒを解除した場合の結果（比較例）の組成推定結果である。各プロットの定義は図７と同様である。
図１０においては、検体「ＳＥ」は、Ｍの含有量は０％にも関わらず１％程度入っているという計算結果となった。０％を１％と推定してしまうと、数％の推定精度もないということになり実用的ではない。

図１１は、「ＭＳＥ＿ｃａｌｉｂ」についてのオリジナルなスペクトル（上、ｒａｗ ｏｆ ＭＳＥ＿ｃａｌｉｂ）と、ＣＣＡ－ｆｉｌｔｅｒを解除した上記で処理を行った後、再構築したスペクトル（下、ｒｅｃｏｎｓｔｒｕｃｔｅｄ ｏｆ ＭＳＥ＿ｃａｌｉｂ）を表す図である。
この結果から、ＣＣＡ－ｆｉｌｔｅｒを解除すると、ＤＯＸ、ＢＧ（図５の説明を参照）のいずれのノイズも除去できていないことがわかった。

図１２は、環境変数による補正を行わなかった場合の組成推定結果である。図１２の結果においては、中実円で表された「Ｎｏｎ－ｃａｌｉｂｒａｔｅｄ」がＫｎｏｗｎからのずれが大きく成っており、環境変数による補正により、得られる推定結果がより正確となることがわかった。

［実施例２］
（エンドメンバーを含まない検体による推定）
学習用検体を含む検体（群）が、エンドメンバーを含まない場合にも精度よく推定できることを確かめるために、表５に記載したサンプルを調製して実施例１と同様の試験を行った。
なお、表中、記号「Ｍ」「Ｓ」「Ｅ」が意味するものは、表４（実施例１）と同様である。また、各サンプルは、単独の成分（ポリマー）の重量分率が８０％を超えないように調整されている。

上記検体について、実施例１と同様の方法で二次元マススペクトルを得て、データ行列に変換した。得られたデータ行列について、すでに説明した１回目のＮＭＦ処理、すなわち、

を実施した。なお、ノイズの分散共分散行列の見積もりは、Ｘのみを用いて計算できるので、１回目のＮＭＦ処理におけるモジュール内部処理とした。

次に、Ａに対するＣＣＡ－Ｆｉｌｔｅｒ、重さや標準ピークによる強度補正を行った。なお、組成分析には温度分布情報は不要なため、温度軸に沿ってサンプル毎に総和を取って、

としてもよい。

次に、

の２回目のＮＭＦ処理を実施した。なお、リーマン計量による評価等は、２回目のＮＭＦ処理の内部処理として実施した。図１５はその結果として、ＣとＢＳとを図示したものである。
図中Ｃでは、本方法によって、推定された組成を丸印で、使用したサンプルの組成（正しい組成）を星印で示している。いずれもよい一致を示している。
ここでは、使用した検体にエンドメンバー、すなわち、Ｅ、Ｓ、Ｍのピュアポリマーが含まれていないことが、Ｃの各頂点にプロットがないことからもわかる。

また、図中ＢＳは、推測によって得られたＥ、Ｍ、Ｓのピュアポリマーのスペクトルと、実測のＥ、Ｍ、Ｓのスペクトルとを重ねて示しているが、両者に差はなく、絶対強度を含めて、よく推定されていることが確かめられた。

このように、本発明の方法によれば、図１５のＢＳに示されたように、Ｅ、Ｍ、Ｓのピュアポリマーのスペクトル、及び、混合物の組成が、正確に推測され得ることが確かめられた。
なお、テストデータがある場合には、Ｘ_ｔｅｓｔをＳとＢに連続射影してＣ_ｔｅｓｔを得る。

［実施例３］
（エンドメンバーを１つ含む検体による推定）
次に、（学習用）検体のうち１つがエンドメンバーを含む場合に、他の検体における成分含有量が任意となる（Ｋ－１次元単体の内接円の外側の領域でなくてもよい）ことを検証した。

表５に記載したサンプルのうち、Ｓを４０質量％以上含むサンプルを除き、かつ、サンプルとしてＭピュアポリマーを加えたこと以外は、実施例２と同様にして、組成推定を行った。図１６は結果である。

図１６において、中実円で表された点は、Ｂ、Ｓの推定に用いた検体の推定結果を表し、星印がその実際の組成である。この結果から、Ｓについては、内接円の外側の領域に検体はなかったものの（中空円は、推定に使用しなかった検体である）、精度よく推定することができることが確認された。
上記原因のひとつは、すでに説明した２回目のＮＭＦ処理（Ｅｑ．１１）において基底の非直交性項

をペナルティー項として組み込んだことによるものと考えらえる。

材料開発の多くの場合で、材料性能を各構成成分に還元して考察することが求められる。これには、成分の同定と定量が必要だが、系が複雑化するほどその難易度は上がる。異なる成分のピークが互いにオーバーラップする可能性が低い高解像度の質量分析は、複雑な混合物系における成分の化学構造を同定するうえで最も強力な分析手法と言える。一方で、質量分析は定量性を有さないことが問題となる。また、本質的には分離を必要としないものの、その結果得られるスペクトルは複雑で現実的には読解不能に陥りやすい。

本発明では、材料の破片を大気下・前処理なしで直接熱分解させ、そこから生じるガスをＤＡＲＴ－ＭＳで分析し、そのスペクトルを教師無し学習することで、各成分のピュアなエンドメンバースペクトルを推定し、その線形和で検体のスペクトルを表す手法を開発した。これは、複雑な組成からなる材料であっても分離を必要とせずに、その成分の同定と定量を可能とする。

同定については、他の成分に由来するピークをすべて排除した可読性の高いエンドメンバースペクトルを得られれば、あとは比較的容易である。一方で、定量分析の妨げとなる、ピークごとにイオン化効率が異なりピーク強度とその存在比が比例しない、という事実は本発明においても同様である。しかし、本発明ではエンドメンバースペクトルの各ピーク強度を、規格化された相対値ではなく、絶対強度として推定できるため、エンドメンバースペクトルの線形和で検体スペクトルを表現する際、その線形係数をそのまま組成比として求めることができる。

検体を成分ごとに分解し、その含有比まで求める本発明は、材料の性能を発揮する要因となったキー成分の同定など、材料開発において重宝されるツールになり得るのは明らかであるが、さらには劣化成分の含有量検査等の品質管理、危険物含有量等の法令順守検査、及び、権利侵害の検出のための検査等、きわめて広範な応用が期待される。さらには樹脂の劣化・寿命予測、樹脂・有機材料における極微不純物成分の検出、嗅覚や味覚の定量分析、食品等のトレーサビリティー・産地偽装防止タグなどの技術が加速すると期待できる。

また、Ｐｌａｓｔｉｃｓ Ｅｕｒｏｐｅは２０２１年９月に欧州委員会に対して２０３０年までにプラスチック容器包装に再生プラスチック３０％含有の義務化を提言するなど、再生材の利用が促進されているが、含有量を測定する一般的手法は確立されていない。本発明はバージン剤と再生材の比率を正確に測定し得る技術としても、品質管理や法令順守検査などへの応用が期待される。

１０：Ｋ－１次元単体、 １２：内接超球、 １３－１５：エンドメンバー、 １６－１８：学習用検体、 １９：領域、 ３０：組成推定装置、 ３１：質量分析装置 、３２：減圧ポンプ、 ３３：情報処理装置、 ３４：プロセッサ、 ３５：記憶デバイス、 ３６：表示デバイス、 ３７：入力デバイス、 ４１：質量分析部、 ４２：情報処理部、 ４３：制御部、 ４４：記憶部、 ４５：入力部、 ４６：出力部、 ４７：データ行列作成部、 ４８：ＮＭＦ処理部、 ４９：補正処理部、 ５０：ベクトル処理部、 ５１：エンドメンバー決定部、 ５２：含有量比計算部

Claims (21)

1. Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の前記成分を含む推定対象検体における、前記成分の含有量比を推定する方法であって、
   前記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、及び、前記成分を含まないバックグラウンド検体を準備することと、
   前記推定対象検体、前記学習用検体、及び、バックグラウンド検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測することと、
   加熱温度ごとに得られた前記マススペクトルを各行に格納し、前記検体ごとの二次元マススペクトルを得て、前記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換することと、
   前記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行うことと、
   前記基底スペクトル行列と前記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、前記ノイズ成分の影響を減ずるよう前記強度分布行列を補正して、補正後強度分布行列を得ることと、
   前記補正後強度分布行列を前記検体のそれぞれに対応する小行列に分割し、前記小行列を特徴ベクトルとして、ベクトル空間内で前記検体のそれぞれを表現することと、
   前記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、前記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定することと、
   前記Ｋ個のエンドメンバーと、前記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、前記ユークリッド距離の比により、前記推定対象検体中の前記成分の含有量比を推定することと、を含み、
   前記Ｋが３以上の場合、前記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、前記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、前記学習用検体が前記エンドメンバーの少なくとも１つを含む、方法。
2. 前記Ｋが２以上の整数であり、前記推定対象検体が、前記成分の混合物である、請求項１に記載の方法。
3. 前記学習用検体が、前記エンドメンバーを含む、請求項１又は２に記載の方法。
4. 前記エンドメンバーの決定が、前記学習用検体に付された判別ラベルに基づき行われる、請求項３に記載の方法。
5. 前記エンドメンバーの決定が、前記学習用検体の前記特徴ベクトルの頂点成分分析によって行われる、請求項３に記載の方法。
6. 前記エンドメンバーの決定が、前記Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムによって実施される、請求項１に記載の方法。
7. 前記エンドメンバーの決定が、前記補正後強度分布行列を非負値行列因子分解し、前記検体中のＫ種類の前記成分の重量分率を表す行列と、Ｋ種類の個別の前記成分ごとのフラグメント存在強度を表す行列との積に分解する第２のＮＭＦ処理により行われる、請求項６に記載の方法。
8. 前記学習用検体が、前記エンドメンバーを含まない、請求項６又は７に記載の方法。
9. 前記補正後強度分布行列を得ることは、更に、前記強度分布行列の強度補正を行うことを含む、請求項１に記載の方法。
10. 前記検体セットが、更に、キャリブレーション検体を含み、
    前記キャリブレーション検体は、前記Ｋ種類の成分を全て含み、かつ、その組成が既知であり、
    前記強度補正は、前記強度分布行列を規格化することを含む、請求項９に記載の方法。
11. 前記強度補正は、前記強度分布行列の少なくとも一部を、前記検体セットのうち対応する前記検体の質量と環境変数の積で割り付けることを含み、
    前記環境変数は、前記観測の際における前記成分のイオン化効率への影響を表す変数である、請求項９に記載の方法。
12. 前記環境変数が、前記観測の際に、雰囲気中に所定量含まれる分子量５０～１５００の化合物、又は、前記検体セットのそれぞれに所定量含まれる分子量５０～５００の有機低分子化合物のマススペクトルのピークの合計値である、請求項１１に記載の方法。
13. Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の前記成分を含む推定対象検体における、前記成分の含有量比を推定する組成推定装置であって、
    前記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、前記成分を含まないバックグラウンド検体、及び、前記推定対象検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測する質量分析装置と、
    前記観測されたマススペクトルを処理する情報処理装置と、を備え、
    前記情報処理装置は、
    加熱温度ごとに得られた前記マススペクトルを各行に格納し、前記検体ごとの二次元マススペクトルを得て、前記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換する、データ行列作成部と、
    前記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行う、ＮＭＦ処理部と、
    前記基底スペクトル行列と前記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、前記ノイズ成分の影響を減ずるよう前記強度分布行列を補正して、補正後強度分布行列を作成する、補正処理部と、
    前記補正後強度分布行列を前記検体セットのそれぞれに対応する小行列に分割し、前記小行列を特徴ベクトルとして、ベクトル空間内で前記検体のそれぞれを表現する、ベクトル処理部と、
    前記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、前記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する、エンドメンバー決定部と、
    前記Ｋ個のエンドメンバーと、前記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、前記ユークリッド距離の比により、前記推定対象検体中の前記成分の含有量比を推定する、含有量比計算部と、を含み、
    前記Ｋが３以上の場合、前記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、前記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、前記学習用検体が前記エンドメンバーの少なくとも１つを含む、組成推定装置。
14. 前記エンドメンバー決定部は、前記学習用検体に付された判別ラベルに基づいて前記エンドメンバーを決定する、請求項１３に記載の組成推定装置。
15. 前記エンドメンバー決定部は、前記Ｋ－１次元単体が最小体積となるように頂点を定めるアルゴリズムによって前記エンドメンバーを決定する、請求項１３に記載の組成推定装置。
16. 前記エンドメンバー決定部は、前記補正後強度分布行列を非負値行列因子分解し、前記検体中のＫ種類の前記成分の重量分率を表す行列と、Ｋ種類の個別の前記成分ごとのフラグメント存在強度を表す行列との積に分解する第２のＮＭＦ処理により前記エンドメンバーを決定する、請求項１５に記載の組成推定装置。
17. 前記補正処理部は更に、前記強度分布行列の強度補正を行う、請求項１５に記載の組成推定装置。
18. 前記検体セットが、更に、キャリブレーション検体を含み、
    前記キャリブレーション検体が、前記Ｋ種類の成分を全て含み、かつ、その組成が既知であり、
    前記強度補正が、前記強度分布行列を規格化することを含む、請求項１７に記載の組成推定装置。
19. 前記強度補正は、前記強度分布行列の少なくとも一部を、前記検体セットのうち対応する前記検体の質量と環境変数の積で割り付けることを含み、
    前記環境変数は、前記観測の際における前記成分のイオン化効率への影響を表す変数である、請求項１７に記載の組成推定装置。
20. 前記質量分析装置は減圧ポンプを更に備え、
    前記環境変数が、前記減圧ポンプの稼働によって生ずる物質のマススペクトルのピークの合計値である、請求項１９に記載の組成推定装置。
21. Ｋを１以上の整数としたとき、Ｋ種類の成分から選択される少なくとも１種の前記成分を含む推定対象検体における、前記成分の含有量比を推定する組成推定装置において用いられるプログラムであって、
    前記Ｋ種類の成分から選択される少なくとも１種の成分を含み、互いに組成の異なるＫ個以上の学習用検体、前記成分を含まないバックグラウンド検体、及び、前記推定対象検体を含む検体セットに含まれるそれぞれの検体を加熱しながら、熱脱着、及び／又は、熱分解によって生ずるガス成分を順次イオン化し、マススペクトルを連続的に観測する質量分析装置と、
    前記観測されたマススペクトルを処理する情報処理装置と、を備え、
    前記質量分析装置によって、加熱温度ごとに取得された前記マススペクトルを各行に格納し、前記検体ごとの二次元マススペクトルを得て、前記二次元マススペクトルの少なくとも２つ以上をまとめてデータ行列に変換する、データ行列作成機能と、
    前記データ行列を非負値行列因子分解し、規格化された基底スペクトル行列とその強度分布行列の積に分解するＮＭＦ処理を行う、ＮＭＦ処理機能と、
    前記基底スペクトル行列と前記データ行列との正準相関分析によって強度分布行列に含まれるノイズ成分を抽出し、前記ノイズ成分の影響を減ずるよう前記強度分布行列を補正して、補正後強度分布行列を作成する、補正処理機能と、
    前記補正後強度分布行列を前記検体のそれぞれに対応する小行列に分割し、前記小行列を特徴ベクトルとして、ベクトル空間内で前記検体のそれぞれを表現する、ベクトル処理機能と、
    前記特徴ベクトルの全てを内包するＫ－１次元単体を設定し、前記Ｋ－１次元単体におけるＫ個のエンドメンバーを決定する、エンドメンバー決定機能と、
    前記Ｋ個のエンドメンバーと、前記推定対象検体の特徴ベクトルとの、ユークリッド距離をそれぞれ計算し、前記ユークリッド距離の比により、前記推定対象検体中の前記成分の含有量比を推定する、含有量比計算機能と、を含み、
    前記Ｋが３以上の場合、前記Ｋ－１次元単体に内接する超球体の外側の領域のそれぞれに、前記学習用検体の特徴ベクトルの少なくとも１つが位置する、又は、前記学習用検体が前記エンドメンバーの少なくとも１つを含む、プログラム。

Images