den kommutative lov – Store norske leksikon

Den kommutative lov er en matematisk lov som blant annet gjelder for addisjon og multiplikasjon. Loven sier at dersom man adderer eller multipliserer to tall, blir resultatet det samme uansett i hvilken rekkefølge man gjør det. For å uttrykke den kommutative loven for multiplikasjon sier man også at faktorenes orden er likegyldig.

Faktaboks

Uttale: kommutatˈive
Etymologi: av latin av commutare, 'veksle, bytte'

Hvis for eksempel Kari gir Per først 3 epler og så 8 epler, så får han det samme som hvis hun først gir ham 8 epler og så 3 epler. I begge tilfeller ender Per opp med å få 11 epler.

Den kommutative loven gjelder ikke for subtraksjon eller divisjon. For eksempel er ikke \(8−3\) det samme som \(3−8\).

Definisjon

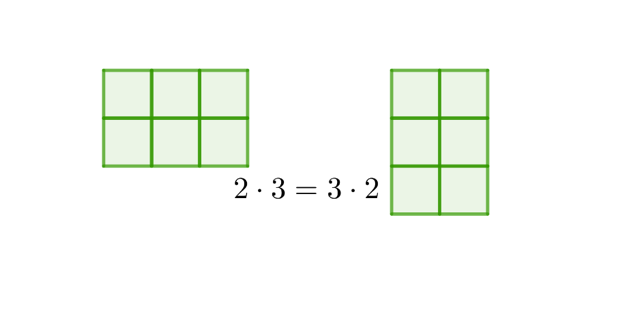
Innen algebra kan den kommutative lov for addisjon defineres som regelen:

\[a + b = b + a\]

Og tilsvarende for multiplikasjon er regelen:

\[a \cdot b = b \cdot a\]

Det vil si at det ikke spiller noen rolle i hvilken rekkefølge man legger sammen tall eller ganger tall med hverandre. Her er a og b vilkårlige reelle tall.

Visualisering

Den kommutative loven for multiplikasjon kan visualiseres med et rektangel som er delt inn i ruter. Den ene faktoren angir antall ruter i lengden, og den andre faktoren angir antall ruter i bredden. Dersom rektangelet blir snudd over på en annen side, endrer ikke antall ruter i rektangelet seg.

Anvendelse

Den kommutative loven kan brukes til å forenkle utregninger. Eksempel:

\(38 + 147 + 42 = 38 + 42 + 147 = 80 + 147 = 227\)

Andre operasjoner

Kommutativitet kan defineres på tilsvarende måte for en rekke andre regneoperasjoner. Regelen kan også gjelde for andre matematiske objekter enn tall, for eksempel vektorer (skalarprodukt) og polynomer.

Moderne algebra har i utstrakt grad beskjeftiget seg med ikke-kommutative systemer, for eksempel grupper hvor den kommutative loven ikke gjelder for multiplikasjon. Slike systemer sies å være antikommutative. For eksempel gjelder ikke den kommutative loven for multiplikasjon av matriser.

I en gruppe kalles elementet c som er bestemt ved ligningen \(a \cdot b = c \cdot b \cdot a\) for kommutatoren til a og b.

Les mer i Store norske leksikon

Kommentarer

Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.

Du må være logget inn for å kommentere.

Fagansvarlig for Aritmetikk

Andrea Hofmann

Førsteamanuensis, Universitetet i Sørøst-Norge