[go: up one dir, main page]
Jump to content

Polygon

From Simple English Wikipedia, the free encyclopedia
(Redirected from Icosidigon)
Polygons: open (excluding its boundary), boundary only (excluding interior), closed (including both boundary and interior), and self-intersecting

A polygon is a closed two-dimensional shape. It is a plane figure that is made up of a number of sides. These are also called edges or line segments. Each side is connected to another one by a corner, or vertex. Each pair of connected sides makes an angle.

These sides and angles can be different from one another, or they can all be the same. Polygons made of only sides of the same length (equilateral) and angles the same width (equiangular) are called regular polygons.

A square is a polygon because it has four sides. The smallest polygon in Euclidean geometry or "flat geometry" is the triangle, which has three sides and three corners. On a sphere, there can also be a digon and a henagon.

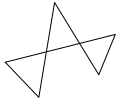
If the edge lines of the polygon do not cross each other, the polygon is called simple; otherwise it is complex.

In computer graphics, polygons (especially triangles) are often used to make graphics.

[change | change source]
  • A complex pentagon
    A complex pentagon
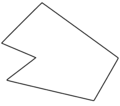
  • A simple concave hexagon
    A simple concave hexagon
  • A non-regular heptagon
    A non-regular heptagon
  • A non-regular octagon
    A non-regular octagon
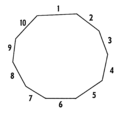
  • A non-regular decagon
    A non-regular decagon
  • A enneacontakaienneagon (a polygon with 99 sides)
    A enneacontakaienneagon (a polygon with 99 sides)

List of polygons

[change | change source]
Polygon names and miscellaneous properties
Name Sides Properties
monogon 1 Not generally recognised as a polygon,[1] although some disciplines such as graph theory sometimes use the term.[2]
digon 2 Not generally recognised as a polygon in the Euclidean plane, although it can exist as a spherical polygon.[3]
triangle (or trigon) 3 The simplest polygon which can exist in the Euclidean plane. Can tile the plane.
quadrilateral (or tetragon) 4 The simplest polygon which can cross itself; the simplest polygon which can be concave; the simplest polygon which can be non-cyclic. Can tile the plane.
pentagon 5 [4] The simplest polygon which can exist as a regular star. A star pentagon is known as a pentagram or pentacle.
hexagon 6 [4] Can tile the plane.
heptagon (or septagon) 7 [4] The simplest polygon such that the regular form is not constructible with compass and straightedge. However, it can be constructed using a Neusis construction.
octagon 8 [4]
enneagon (or nonagon) 9 [4] "Nonagon" mixes Latin [novem = 9] with Greek; "enneagon" is pure Greek.
decagon 10 [4]
hendecagon (or undecagon) 11 [4] The simplest polygon such that the regular form cannot be constructed with compass, straightedge, and angle trisector.
dodecagon (or duodecagon) 12 [4]
tridecagon (or trisdecagon) 13 [4]
tetradecagon 14 [4]
pentadecagon (or quindecagon) 15 [4]
hexadecagon (or hexakaidecagon) 16 [4]
heptadecagon (or septadecagon) 17 Constructible polygon
octadecagon 18 [4]
enneadecagon (or nonadecagon) 19 [4]
icosagon 20 [4]
icositetragon (or icosikaitetragon) 24 [4]
triacontagon 30 [4]
tetracontagon (or tessaracontagon) 40 [4][5]
pentacontagon (or pentecontagon) 50 [4][5]
hexacontagon (or hexecontagon) 60 [4][5]
heptacontagon (or hebdomecontagon) 70 [4][5]
octacontagon (or ogdoëcontagon) 80 [4][5]
enneacontagon (or enenecontagon) 90 [4][5]
hectogon (or hecatontagon) 100 [4]
257-gon 257 Constructible polygon
chiliagon 1,000 Philosophers including René Descartes,[6] Immanuel Kant,[7] David Hume,[8] have used the chiliagon as an example in discussions.
myriagon 10,000 Used as an example in some philosophical discussions, for example in Descartes's Meditations on First Philosophy
65537-gon 65,537 Constructible polygon
megagon[9][10][11] 1,000,000 As with René Descartes's example of the chiliagon, the million-sided polygon has been used as an illustration of a well-defined concept that cannot be visualised.[12][13][14][15][16][17][18] The megagon is also used as an illustration of the convergence of regular polygons to a circle.[19]
apeirogon ∞ A degenerate polygon of infinitely many sides.

References

[change | change source]
  1. ↑ Grunbaum, B.; "Are your polyhedra the same as my polyhedra", Discrete and computational geometry: the Goodman-Pollack Festschrift, Ed. Aronov et al., Springer (2003), p. 464.
  2. ↑ Hass, Joel; Morgan, Frank (1996), "Geodesic nets on the 2-sphere", Proceedings of the American Mathematical Society, 124 (12): 3843–3850, doi:10.1090/S0002-9939-96-03492-2, JSTOR 2161556, MR 1343696
  3. ↑ Coxeter, H.S.M.; Regular polytopes, Dover Edition (1973), p. 4.
  4. ↑ 4.00 4.01 4.02 4.03 4.04 4.05 4.06 4.07 4.08 4.09 4.10 4.11 4.12 4.13 4.14 4.15 4.16 4.17 4.18 4.19 4.20 4.21 4.22 4.23 Salomon, David (2011). The Computer Graphics Manual. Springer Science & Business Media. pp. 88–90. ISBN 978-0-85729-886-7.
  5. ↑ 5.0 5.1 5.2 5.3 5.4 5.5 Peirce, Charles Sanders (1976). The New Elements of Mathematics: Algebra and geometry. Mouton Publishers. p. 298. ISBN 978-0-391-00612-6.
  6. ↑ Sepkoski, David (2005). "Nominalism and constructivism in seventeenth-century mathematical philosophy" (PDF). Historia Mathematica. 32: 33–59. doi:10.1016/j.hm.2003.09.002. S2CID 120467581. Archived from the original (PDF) on 12 May 2012. Retrieved 18 April 2012.
  7. ↑ Martin, Gottfried (1955). Kant's Metaphysics and Theory of Science. Manchester University Press. p. 22.
  8. ↑ Hume, David (1826). The Philosophical Works: Including All the Essays, and Exhibiting the More Important Alterations and Corrections in the Successive Ed. Publ. Black and Tait. p. 101.
  9. ↑ Gibilisco, Stan (2003). Geometry demystified (Online-Ausg. ed.). New York: McGraw-Hill. ISBN 978-0-07-141650-4.
  10. ↑ Darling, David (2004). The Universal Book of Mathematics: From Abracadabra to Zeno's Paradoxes. Wiley. p. 249. ISBN 978-0-471-66700-1.
  11. ↑ Dugopolski, Mark (1999). College Algebra and Trigonometry. Addison-Wesley. p. 505. ISBN 978-0-201-34712-8.
  12. ↑ McCormick, John Francis (1928). Being, its division and causes. Loyola University Press. p. 18.
  13. ↑ Merrill, John Calhoun; Odell, S. Jack (1983). Philosophy and Journalism. Longman. p. 47. ISBN 978-0-582-28157-8.
  14. ↑ Hospers, John (1997). An Introduction to Philosophical Analysis. Psychology Press. p. 56. ISBN 978-0-415-15792-6.
  15. ↑ Mandik, Pete (2010). Key Terms in Philosophy of Mind. A&C Black. p. 2010. ISBN 978-1-84706-349-6.
  16. ↑ Kenny, Anthony (2006). The Rise of Modern Philosophy: A New History of Western Philosophy. Oxford University Press. p. 124. ISBN 978-0-19-875277-6.
  17. ↑ BALMES, REV JAMES (1856). FUNDAMENTAL PHILOSOPHY. p. 27.
  18. ↑ Potter, Vincent G. (1993). On Understanding Understanding: A Philosophy of Knowledge. Fordham University Press. p. 86. ISBN 978-0-8232-1486-0.
  19. ↑ Russell, Bertrand (2004). History of Western Philosophy. Psychology Press. p. 202. ISBN 978-0-415-32505-9.
Retrieved from "https://simple.wikipedia.org/w/index.php?title=Polygon&oldid=9356959"