JP4464657B2 - 曲面画像処理装置及び曲面画像処理方法 - Google Patents
曲面画像処理装置及び曲面画像処理方法 Download PDFInfo
- Publication number
- JP4464657B2 JP4464657B2 JP2003380341A JP2003380341A JP4464657B2 JP 4464657 B2 JP4464657 B2 JP 4464657B2 JP 2003380341 A JP2003380341 A JP 2003380341A JP 2003380341 A JP2003380341 A JP 2003380341A JP 4464657 B2 JP4464657 B2 JP 4464657B2
- Authority
- JP
- Japan
- Prior art keywords
- curved surface
- control point
- patch
- image processing
- curved
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06T—IMAGE DATA PROCESSING OR GENERATION, IN GENERAL
- G06T17/00—Three dimensional [3D] modelling, e.g. data description of 3D objects
- G06T17/30—Polynomial surface description
Landscapes
- Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- General Physics & Mathematics (AREA)
- Pure & Applied Mathematics (AREA)
- Mathematical Optimization (AREA)
- Mathematical Physics (AREA)
- Mathematical Analysis (AREA)
- Algebra (AREA)
- Computer Graphics (AREA)
- Geometry (AREA)
- Software Systems (AREA)
- Theoretical Computer Science (AREA)
- Image Generation (AREA)
Description
まず最初に、(A)として、NURBSデータを用いて曲面画像を生成する処理全体における背景技術についての説明を行う。
図3(a)及び(b)はNURBS曲線及びNURBS曲面例を示す図である。NURBS曲線31は、パラメータuを媒介変数としたパラメトリック曲線であり、その曲線形状は、複数の制御点列32と、各制御点における重みwと、パラメータuの変化に伴う各制御点の影響力の変化を表すノットの列であるノットベクトルによって操作される。また、NURBSデータの各制御点32はNURBS曲線31上の点とは限らない。
一般的にNURBS曲面S(u、v)は(数1)で表される。
従来、NURBSデータの画像処理において、これらの数式に関する演算量は非常に多く、リアルタイム性を求められる画像処理システムでは表現できるNURBSデータ量が限られてしまうという問題点を有している。さらに、NURBSデータを用いた画像処理をハードウェア化する場合に回路規模が大きくなり、小型化の妨げとなっている。
この曲面画像処理装置においては、(数2)、(数3)の漸化式を再帰的に計算せずに、一般3次式に展開し、ノットベクトルを代入することでBスプライン基底関数を求めるための係数マトリックス(4×4)を算出する。これらの係数マトリックスは、NURBS曲面を定義する全ての制御点列に対して算出しておく。一方、リアルタイム処理では、パラメータu、vを変化させながら、制御点データと係数マトリックスを用いてNURBS曲面上の各点を計算するようにしている。
最初に、ベジエ(Bezier)曲面やB−スプライン(B−Spline)曲面等のパラメットリック曲面について一般的な定義を述べておく。自由曲面の種類としては、ベジエ(Bezier)曲面やB−スプライン(B−Spline)曲面等いくつかの種類があるが、より一般的な自由曲面の表現形式としてNURBS曲面が広く用いられている。パラメトリック曲面は3次元空間において、2つの媒介変数(u,v)により曲面上の点(x,y,z)が連続的に定義される。
<P> = (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j] * <Q[i][j]>)
/ (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j])
すなわち、
px = (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j] * qx[i][j])
/ (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j])
py = (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j] * qy[i][j])
/ (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j])
pz = (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j] * qz[i][j])
/ (ΣΣ B[n][i](u) * B[m][j](v) * qw[i][j])
但し、i = 0, 1, 2, ... , (I-1)、j = 0, 1, 2, ... , (J-1)とし、記号Σはこの範囲のi及びjについて和をとることを示す。ここでIはu方向の制御点数、Jはv方向の制御点数である。またn及びmは、u方向及びv方向の基底関数の次数である。
このノットベクトルとは、媒介変数の取り得る値を、曲面の形状を特徴づけるような、ある間隔を持って小さい方から順に並べたものである。媒介変数u,vそれぞれの方向に対し、異なる次数と異なるノットベクトルを用いて異なる基底関数を定義することができる。NURBS曲面の基底関数B[n][i](u)及びB[m][j](v)は、u方向のノットベクトル(u[0], u[1], ... , u[I+n+1])及びv方向のノットベクトル(v[0], v[1], ... , v[J+m+1])を用いて、以下のCox−deBoorの漸化式で表される。すなわちu方向について、
B[n][i](u) = [(u - u[i]) / (u[i+n] - u[i])] * B[n-1][i](u)
+ [(u[i+n+1] - u) / (u[i+n+1] - u[i+1])] * B[n-1][i+1](u)
である。但し、上式において次数nは0でない。上式は漸化式であるから、例えばn=3の基底関数は、n=2の基底関数により求められる。これを繰り返すとn=0の基底関数が必要になるが、n=0のときの基底関数B[0][i](u)は、uの範囲が(u[i], u[i+1])の間にあるときに限り値1をとり、それ以外では値0をとるものとする。また、ノットベクトルの要素はインデックスが増すごとに値が等しいか単調増加であり、前記の漸化式中の分数で表される係数部分は、分母が0となる場合は0と定義される。ちなみに前記の漸化式は、次数の代わりに階数を用いて表現しても良い。階数は次数nに1を加えた値である。また、v方向についても同様に、以下の基底関数が定義される。
+ [(v[j+m+1] - v) / (v[j+m+1] - v[j+1])] * B[m-1][j+1](v)
さて、NURBS曲面をポリゴンに分割するとき、上に示したような漸化式に必要なパラメータを代入し、曲面上の3次元座標<P> = (px, py, pz)を求める必要がある。
/ (Σ B[n][i](u) * qw[i])
px = (Σ B[n][i](u) * qw[i] * qx[i])
/ (Σ B[n][i](u) * qw[i])
py = (Σ B[n][i](u) * qw[i] * qy[i])
/ (Σ B[n][i](u) * qw[i])
図19及び上式では視覚的に分かりやすい2次元空間でNURBS曲線を定義しているが、Z座標pzも定義して3次元空間におけるNURBS曲線であってもよい。ちなみに、ノットベクトルの要素数と次数及び制御点数との関係は、次数n、制御点数Iとすると、ノットベクトルの要素数(I+n+1)で求めることができる。図19の場合、4+3+1=8である。また図19において、NURBS曲線1901が描かれるノットベクトルの有効範囲は(u[3], u[4])の範囲である。このように、次数n=3のNURBS曲線を描くためには少なくとも4つの制御点が必要となる。次数n=3を一定にして、制御点を1つ増やすと、ノットベクトルの要素も1つ増え、NURBS曲線が描かれるノットベクトルの有効範囲は(u[3], u[5])と拡大していく。この様子を図20に示す。尚、図19及び図20からも分かるように、一般的にNURBS曲線は制御点を通過しない。但し、後述するように、ノットベクトルの並びが有理ベジエ曲線を表すような場合には、制御点を端点に持つようになる。
現在、パラメトリックな曲面を含む3次元オブジェクトを2次元の画像表示装置に表示する方法として、オブジェクトを多数の微小な平面ポリゴンの集合体に近似してレンダリングする方法が一般的に用いられている。
パラメトリック曲面をポリゴンに分割する一般的な方法としては、定義されたパラメトリック曲面の方程式において媒介変数の値を一定の間隔を持って離散的に変化させることによりパラメットリック曲面上の点を直接求め、これらの点を隣接するものどうし複数組み合わせて平面的なポリゴンを生成するという方法が用いられる。このような処理を一般的にテッセレーションと言う。
また、図49に示すように、制御点の端点を結んでエッジを生成し、エッジの中点からポリゴンの表面を表現する曲面上の中点へのベクトルを算出し、これを弦の偏移ベクトルとする。そして、弦の偏移ベクトルを透視変換した時のスクリーン上におけるベクトル長に応じて、解像度の量を決定する方法もある(例えば、特許文献4参照)。
NURBS曲面を用いてノット挿入を行いパラメータ変換されたベジエ曲面は、(n+1)×(n+1)個の制御点が与えられると、双n次のベジエ曲面を構成する。ここでは単にn次のベジエ曲面と呼ぶ。そして、三次元コンピュータ・グラフィックスの分野においては、曲面の制御のしやすさから三次のベジエ曲面が多用される(例えば、非特許文献4参照)。
或いは、他の描画方法として、隣接する制御点間に対して座標を平均することで新たな制御点を発生させるという処理を繰り返す、いわゆる細分割法と呼ばれる方法により多角形で近似して描画されることもある(例えば、特許文献6参照)。
また、入力データは3次のNURBS曲面に限定されるという問題を有していた。さらに、差分マトリックスを用いた場合、各パラメータu、vの増分は一定値(Δu、Δv)に限定されてしまうという問題を有している。またさらに、厳密にNURBS曲面を表現しようとすると、係数マトリックスを有理化する必要があるため、算出したNURBS曲面上の各点を除算する必要があり除算による演算量が増加してしまうという問題を有している。
但し、上式においてiは0でない。i=0の場合は以下で表される。
<Q'[0]> = a[0] * <Q[0]>
ここで、上式に含まれる係数配列a[i]は次式で表される。
a[i] = 1 (iがk−n以下のとき)
a[i] = 0 (iがk+1以上のとき)
a[i] = (〜u - u[i]) / (u[i+n] - u[i]) (iがそれ以外のとき)
例えば、初期の制御点列を(Q[0], Q[1], Q[2], Q[3])、初期のノットベクトルを(u[0], u[1], ... , u[7])とし、ノットu[3]とu[4]の間に、値がu[3]に等しい新しいノット〜uを1つ挿入するとき、新しい制御点列(Q'[0], Q'[1], ... , Q'[4])は以下のようになる。すなわち、ノットの挿入位置はk=3であるから、係数配列は
a[0] = 1
a[1] = (〜u - u[1]) / (u[4] - u[1]) = (u[3] - u[1]) / (u[4] - u[1])
a[2] = (〜u - u[2]) / (u[5] - u[2]) = (u[3] - u[2]) / (u[5] - u[2])
a[3] = (〜u - u[3]) / (u[6] - u[3]) = 0
a[4] = 0
であって、これらを用いて
<Q'[0]> = a[0] * <Q[0]> = <Q[0]>
<Q'[1]> = (1 - a[1]) * <Q[0]> + a[1] * <Q[1]>
<Q'[2]> = (1 - a[2]) * <Q[1]> + a[2] * <Q[2]>
<Q'[3]> = (1 - a[3]) * <Q[2]> + a[3] * <Q[3]> = <Q[2]>
<Q'[4]> = (1 - a[4]) * <Q[3]> + a[4] * <Q[4]> = <Q[3]>
となる。これは、初期の制御点<Q[1]>が消え、新しい位置<Q'[1]>及び<Q'[2]>に制御点が生成されたことを示す。
不要な制御点が生じる第一例として、図19のNURBS曲線1901は、次数n=3であり、制御点列(Q[0], Q[1], Q[2], Q[3])及びノットベクトル(u[0], u[1], ... , u[7])で定義されている。すなわち、制御点数は4であり、ノットベクトルの要素数は8である。但し、全ての異なるインデックスi、j(i<j)に対してu[i]<u[j]であると仮定する。ここで、図23のように、初期のノットベクトル(u[0], u[1], ... , u[7])に、1つずつノットを挿入していき、最終的なノットベクトルが(u'[0], u'[1], u'[2], ...)となったとする。ここで以下の関係を満たせば、生成された最終的なNURBS曲線は、形状を変えずに1つの有理ベジエ曲線に等価変換される。
u[1] = u'[1]
u[2] = u'[2]
u[3] = u'[3] = u'[4] = u'[5]
u[4] = u'[6] = u'[7] = u'[8]
u[5] = u'[9]
u[6] = u'[10]
u[7] = u'[11]
すなわち、NURBS曲線の初期のノットベクトルの有効範囲が(u[3], u[4])であるから、この範囲内のノットu[3]及びu[4]が、それぞれ多重度3となるように(次数n=3に等しくなるように)ノットを挿入していき、最終的なノットベクトル(u'[0], u'[1], u'[2], ... , u'[11])を得る。この例では、新たなノットが4つ挿入されたことになる。従って、最終的な制御点数も4増加して8となって、最終的な制御点列は(Q'[0], Q'[1], ... , Q'[7])となる。このようなノットの並び方で定義されるNURBS曲線は、有理ベジエ曲線と等価であり、元のNURBS曲線と形状が完全に一致することが知られている。ここで、「ノット挿入後の最終的な制御点数」は8であるが、「有理ベジエ曲線を定義する制御点数」は4であるので、最終的な制御点列のうち有理ベジエ曲線を表すのに4つの制御点が不要であることが分かる。
u[1] = u'[1]
u[2] = u'[2]
u[3] = u'[3] = u'[4] = u'[5]
u[4] = u'[6] = u'[7] = u'[8]
u[5] = u'[9] = u'[10] = u'[11]
u[6] = u'[12]
u[7] = u'[13]
u[8] = u'[14]
すなわち、NURBS曲線の初期のノットベクトルの有効範囲が(u[3], u[5])であるから、この範囲内のノットu[3]、u[4]及びu[5]が、それぞれ多重度3となるように(次数n=3に等しくなるように)ノットを挿入していき、最終的なノットベクトル(u'[0], u'[1], u'[2], ... , u'[14])を得る。すなわち、「ノット挿入後の最終的な制御点数」はノットベクトルの要素数15より4小さい11である。この場合、元のNURBS曲線は連続する2つの有理ベジエ曲線に分割される。但し、この2つの有理ベジエ曲線は接続部で制御点を1つ共有しているので、「有理ベジエ曲線を定義する制御点数」は4×2−1=7である。従って、ここでも4つの制御点が不要であることが分かる。
u[1] = u'[1]
u[2] = u[3] = u'[2] = u'[3] = u'[4]
u[4] = u'[5] = u'[6] = u'[7]
u[5] = u'[8] = u'[9] = u'[10]
u[6] = u'[11]
u[7] = u'[12]
u[8] = u'[13]
すなわち、NURBS曲線の初期のノットベクトルの有効範囲が(u[3], u[5])であり、かつu[2]=u[3]であるから、u[3]についてはu[2]も含めて多重度3となるように、u[4]及びu[5]についてもそれぞれ多重度3となるようにノットを挿入していき、最終的なノットベクトル(u'[0], u'[1], u'[2], ... , u'[13])を得る。ここで、「ノット挿入後の最終的な制御点数」は14−4=10であるが、「有理ベジエ曲線を定義する制御点数」は4×2−1=7であるので、この例では3つの制御点が不要であることが分かる。
不要な制御点が生じる第四の例としてNURBS曲面の場合を説明するが、NURBS曲面の場合は、制御点が2次元配列で定義されており、基底関数のパラメータである次数及びノットベクトルが、それぞれu方向及びv方向に定義されている。従って、u方向及びv方向それぞれについてノット挿入を行うことでNURBS曲面を有理ベジエ曲面に等価変換することが可能である。
u[1] = u'[1]
u[2] = u'[2]
u[3] = u'[3] = u'[4] = u'[5]
u[4] = u'[6] = u'[7] = u'[8]
u[5] = u'[9] = u'[10] = u'[11]
u[6] = u'[12]
u[7] = u'[13]
u[8] = u'[14]
v[0] = v'[0]
v[1] = v'[1]
v[2] = v[3] = v'[2] = v'[3] = v'[4]
v[4] = v'[5] = v'[6] = v'[7]
v[5] = v'[8] = v'[9] = v'[10]
v[6] = v'[11]
v[7] = v'[12]
v[8] = v'[13]
従って、「ノット挿入後の最終的な制御点数」は、u方向に11個、v方向に10個であるので11×10=110個である。一方、「有理ベジエ曲面が定義される制御点数」は、u方向に7個、v方向に7個であるので、7×7=49個である。従って、捨てるべき不要な制御点は110−49=61個となる。
また、初期ノットベクトルの並び方、特に初期ノットベクトルの有効範囲におけるノットの多重度によっては、この不要な制御点数が変化するため、これらの規則を一般化する必要がある。
また、上述した特許文献4においては、弦の偏移ベクトルはオブジェクトのシルエットエッジを形成するパッチ(以降、シルエットエッジ形成パッチと称して説明を行う)を検出する指標としては利用することができない。
さらに、上述した特許文献5、又は特許文献6の方法では、最終的に画像生成する際に、曲面上にのる制御点のみを用いる場合には、不用となる制御点に対しても、法線の計算が途中で行われ、演算量が増加するという問題が生じる。
また、本発明は、NURBSデータを用いてノット挿入により有理ベジエデータに変換した後に、サブディビジョン法によりポリゴン分割を行う演算手順においても、より効率的に画像処理における演算量を低減できる曲面画像処理装置を提供することを第二の目的とする。
またさらに、本発明は、ベジェ曲面等の曲面上にのる制御点の情報を用いて法線計算を行う場合においても、頂点となる曲面の四隅の制御点の法線計算に適した方法で、効率的に正しい法線を算出できる曲面画像処理装置を提供することを第四の目的とする。
従って、NURBSデータのままでは演算量が大きく細分割することはできないが、NURBSデータをベジェデータにパラメータ変換するデータ変換部を備えることにより、曲面画像処理装置における3次元オブジェクトの描画処理における演算量を効率的に軽減することができ、より短時間で高精度の描画処理を行うことができる。
従って、NURBSデータのベジェデータへのパラメータ変換処理において生じる不要な制御点を適切に削除してから細分割処理を行うこととなるために、余分な演算を減らして効率的な3次元オブジェクトの描画処理を行うことが可能となる。
従って、細分割手段により細分割された有理ベジェ曲面の輪郭部となるシルエットエッジを検出して、シルエットエッジをなす曲面パッチの細分割レベルを高くすると共に、シルエットエッジとならない曲面パッチの細分割レベルを低くすることにより、従来までの余分な細分割演算を省略すると共に、エッジ部を高レベルに細分割することにより、より高精度に描画処理を行うことができる。また、細分割レベルの決定において、符号付面積の値を用いることで、より効果的に曲面パッチの細分割を行うことができる。
従って、細分割処理後の曲面パッチの制御点の法線の計算において、他の制御点に縮退しているような制御点は法線ベクトルの計算においては選択されないため、より正確に有理ベジェ曲面をなす各制御点の法線の計算を行うことができ、3次元オブジェクトの輝度等の描画処理をより高精度に行うことが可能となる。
そして、本発明に係る曲面画像処理装置によれば、NURBS制御点データを有理ベジェ制御点データに変換する際に生じる不要な制御点を制御点トリミング部により削除することができる。従って、NURBS曲面から有理ベジエ曲面へ変換する際、不要なデータが発生しないので、後段の曲面パッチ分割処理部におけるサブディビジョンによるポリゴン分割を効率よく行うことができる。
さらに、画面に表示されるオブジェクトのシルエットエッジを形成するパッチであるか否かを判定するシルエットエッジ検出部を備えるために、シルエットエッジ部の細分割を適切に行うと共に、シルエットエッジ部以外の曲面パッチの細分割における計算量を軽減させて、細分割における必要な計算負荷を最小限に抑えて、無駄なポリゴン分割を抑制しつつ、エッジ部分の滑らかなオブジェクトを生成することが可能である。
従って、ベジエ曲面の四隅の制御点に対して、隣接する制御点が法線の計算対象の制御点と縮退して同じとなる場合ににおいても、適切な制御点を選択して法線を算出することができる。これら計算は、ベクトルの差の計算と外積を用いるだけで効率的に正確に行うことができる。
図1は実施の形態1における曲面画像処理装置100の機能ブロック図を示している。
この曲面画像処理装置100は、NURBSデータを入力するデータ入力部101、NURBSデータに座標変換を施す座標変換部102、各描画フレームのアニメーションデータを制御するアニメーション制御部103、NURBSデータを有理ベジェデータに変換するデータ変換部104、有理ベジェ曲面パッチを細分割する曲面パッチ分割処理部105、分割後の曲面パッチの制御点に対する法線ベクトルの算出を行う法線計算部106、分割後の曲面パッチに透視変換を施す透視変換部107、及び曲面パッチに対しレンダリング処理を行うレンダリング処理部108を備える。
はじめに、本発明の実施の形態1に係る曲面画像処理装置100におけるNURBSデータ及び有理ベジェ制御点データとその扱い方について説明する。
一般的に、3次元のユークリッド空間における通常座標系を用いると、NURBSデータ及び有理ベジェ制御点データにおける任意の制御点と重みは、P(x、y、z)とwの組みで表される。
最初に、データ入力部101はNURBSデータを座標変換部102に入力する(S201)。
そして、座標変換部102においては、アニメーション制御部103から入力されるアニメーションデータの視点、視線の情報を用いて、NURBSデータに対し、モデリング変換、視野変換、3次元空間におけるクリッピング処理を行い、視野座標系におけるNURBSデータを算出する(S203)。
次に、曲面パッチ分割処理部105は、曲面パッチの細分割の結果、各曲面パッチが充分な平坦度を有しているか否かを、現在の視点から有理ベジェ曲面パッチまでの距離を用いて判断し、再度分割処理が必要な場合には再度有理ベジェパッチの分割処理を行い(S206でN)、一方、全ての有理ベジェ曲面パッチが充分に細分割された場合においては(S206でY)、透視変換部107は、各有理ベジェ曲面パッチを制御点データを頂点としたポリゴンデータに近似して変換する(S207)。
ところで、NURBS曲面は、非一様(Non Uniform)な有理(Rational)Bスプライン曲線の集合によって形成される。たとえば図3(b)において、NURBS曲面33は、パラメータu、vを媒介変数とした2方向のNURBS曲線の集合から成る。
次に、曲面パッチ分割処理部105において、ド・カステリョのアルゴリズムを用いて有理ベジェ曲面パッチを分割する方法について説明する。
一般的に、3次元ユークリッド空間において、有理ド・カステリョのアルゴリズムを用いると、1つのセグメント51は、各制御点を結ぶ直線B1B2、B2B3、B3B4を、0<t<1、i=1、2、3、4について、wi+1*t:wi*(1−t)の比率で内分する点をC1、C2、C3とし、それぞれにおける重みw'i=wi*(1−t)+wi+1*tとし、
更に、直線C1C2、C2C3を、i=1、2、3について、
w'i+1*t:w'i*(1−t)の比率で内分する点をD1、D2とし、それぞれにおける重みw"i=w'i*(1−t)+w'i+1*tとし、
更に、i=1、2について、直線D1D2を、
w"i+1*t:w"i*(1−t)の比率で内分する点をB5とし、
W5=w"i*(1−t)+w"i+1*tとした場合、
B5はセグメント51上の点となり、算出されたw5はB5における重みとなることが知られている。ここでB1、C1、D1、B5はセグメントB1B5の制御点であり、B5、D2、C3、B4はセグメントB5B4の制御点である。
図6は射影空間における3次のセグメントに、ド・カステリョのアルゴリズムを用いた例である。図6において、B1、B2、B3、B4はセグメント61を形成する制御点データであり、B1、B4は端点となる。
その結果、セグメント61はB1B5と、B5B4の2つのセグメントに分割される。新たに作成されたセグメントB1B5の制御点は、B1、C1、D1、B5であり、セグメントB5B4の制御点は、B5、D2、C3、B4である。
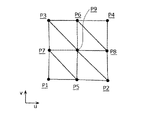
図7は、3次の有理ベジェ曲面パッチ71を16個の制御点データを用いて表した参考図である。図7においてP1、P2、P3、P4は端点であり、各端点は曲面パッチ上の点である。
ステップ205によって、とくにセグメントP3P4を分割してえられた点P6と、セグメントP1P2を分割してえられた点P5は、有理ベジェ曲面パッチ71上の点となる。すなわち、有理ベジェ曲面パッチ71は、P1、P5、P6、P3を端点とする有理ベジェ曲面パッチ81と、P5、P2、P4、P6を端点とする有理ベジェ曲面パッチ82の2つに分割される。
ここでは、新たに有理ベジェ曲面パッチ上の点P7、P8、P9が算出され、有理ベジェ曲面パッチ81は、P7、P9、P6、P3を端点とする有理ベジェ曲面パッチ91と、P1、P5、P9、P7を端点とする有理ベジェ曲面パッチ92とに分割され、有理ベジェ曲面パッチ82は、P9、P8、P4、P6を端点とする有理ベジェ曲面パッチ93と、P5、P2、P8、P9を端点とする有理ベジェ曲面パッチ94とに分割される。
ところで、これらのポリゴンデータの頂点は射影空間における点であるため、レンダリングを行うためには、3次元ユークリッド空間における点に変換する必要がある。
さらに、NURBSデータ及び有理ベジェ制御点データの制御点と重みを制御点データとして同次座標系で扱うことにより、透視変換部107におけるレンダリング処理前の射影変換と透視変換とを一括して行えるため、射影変換に伴う重みによる除算を省略することができ、高速にNURBS曲面をレンダリングすることが可能となる。
以下、本発明の実施の形態2について、図面を用いて説明する。
本実施の形態2における曲面画像処理装置100の機能ブロック図は、上述した実施の形態1と同様であり、アニメーション制御部103において算出されるアニメーションデータは座標変換部102及びデータ変換部104に入力されることを特徴とする。
最初に、図11を用いて本実施の形態2の曲面画像処理装置100の動作を説明する。本実施の形態2では、本発明の実施の形態1と同様に、NURBSデータ及び有理ベジェ制御点データについては、制御点と重みを一括して制御点データと呼び、射影空間における同次座標系を用いて扱う。
最初に、データ入力部101はNURBS制御点、各制御点における重み、ノットベクトルから成るNURBSデータをデータ変換部104に入力する(S1101)。
次に、データ変換部104は、データ入力部101から入力されたNURBSデータを形成する各NURBS曲線に対し、ノットを挿入することによって、セグメントから成る区分有理ベジェ曲線に変換する(S1102)。
また、座標変換部102は、アニメーション制御部103から得られた現フレームのアニメーションデータの視点、視線の情報を用いて、データ変換部101で算出された各セグメントを形成する有理ベジェ制御点データに対し、モデリング変換、視野変換、3次元空間におけるクリッピング処理を行い、視野座標系におけるセグメントを形成する有理ベジェ制御点データを算出する(S1104)。
そして、曲面パッチ分割処理部105は、現在の分割結果が充分かどうかを、現在の視点から有理ベジェ曲面パッチまでの距離を用いて判断し、再度分割処理が必要な場合にはステップ1105に戻る(S1106でN)。
そして、透視変換部107は、得られたポリゴンデータの各頂点に対する射影変換と透視変換を一括して行い(S1109)、また、レンダリング処理部108は、現在の光源情報を用いてポリゴンデータにシェーディング処理やテクスチャマッピング処理等のレンダリング処理(S1110)を行った後、次のフレームの描画処理のために、ステップ1101に戻る。尚、ステップ1102までの処理は、前処理として1度だけ実行され、ステップ1103からステップ1110までの処理は描画フレームごとに繰り返し実行される。
また、本実施の形態2においては、座標変換部102による視野座標変換は、データ変換部104によって得られた有理ベジェ制御点データに対して行ったが、予め視野座標変換を行わずに、曲面パッチ分割処理部105で得られる分割後の有理ベジェ曲面パッチを形成する有理ベジェ制御点データに対して視野座標変換を行ってもよい。
以下、本実施の形態3の曲面画像処理装置100について説明する。尚、本実施の形態3における曲面画像処理装置100の機能ブロック図は上述した実施の形態1と同様となるため、その詳細な説明を省略する。
次に、曲面画像処理装置100の曲面パッチ分割処理部105の構成とその動作について説明する。
まず、セグメント分配部1201は、データ変換部104から得られた有理ベジェ曲面パッチを形成するセグメントの中から分割処理待ちのセグメントを1つ選択する(S1301)。
そして、セグメントがv方向である場合には(S1303でY)、セグメント分配部1201は、選択したセグメントと同一パッチ内におけるu方向の同一レベルの分割処理が全て終わっているかどうかを判断する。終わっている場合には(S1304でY)、セグメント分配部1201は、処理待ち状態のいずれかのセグメント分割部1202にセグメントを入力する(S1305)。
以上のように、本発明の実施の形態3によれば、セグメント分配部1201と、1つの3次有理ベジェ曲面を形成する有理ベジェ制御点データから分割された2つの3次有理ベジェ曲面を形成する有理ベジェ制御点データを算出するセグメント分割部1202を少なくとも1つ以上備えた曲面パッチ分割処理部105を設けることにより、同時に処理可能なセグメントの分割処理を並列に実行することによって、曲面パッチの分割処理を高速に実現することができるため、滑らかで高画質なNURBS曲面を、リアルタイムにレンダリングすることが可能な高性能な曲面画像処理装置100を構成することができる。
また、上述の実施の形態1から3において、曲面パッチ分割処理部105では、ド・カステリョのアルゴリズムに対し、t=1/2を適用したが、t=1/(2のn乗)を適用してもよい(但し、nは正整数)。さらに、曲面パッチ分割処理部105では、パラメータu方向に分割を行った後、パラメータv方向に分割を行ったが、パラメータv方向に分割を行った後、パラメータu方向に分割を行っても良い。
さらに、各有理ベジェ曲面パッチ単位でポリゴンデータへの変換を行ったがパッチをまたがるポリゴンデータに変換してもよい。例えば、曲面パッチ91、92、93、94を、P4P3P1、P4P1P2の2つのポリゴンデータへ変換してもよい。
次に、実施の形態4に係る曲面画像処理装置100の説明を行う。
本実施の形態4の曲面画像処理装置100においては、曲面パッチ分割処理部105において曲面パッチを細分割する際に、従来のようにNURBS曲面上の点を直接求めるのではなく、データ変換部104においてNURBS曲面を有理ベジエ曲面に等価変換して曲面上の制御点を求めてから細分割する。従って、データ変換部104におけるノット挿入の際に不要な制御点が生じるという課題が発生するが、本実施の形態4に係る曲面画像処理装置100において、これを解決するものである。
本実施の形態4においては、データ変換部104は、ノット挿入部1401、制御点トリミング部1402、及び有理ベジエ制御点データ決定部1403を備える。
データ変換部104に入力されるNURBSモデルデータは、NURBS曲面を記述するモデルデータである。ここで、NURBSモデルデータは、NURBS曲面上の点の位置座標は含んでおらず、NURBS曲面を表す情報量としては最小限であると言える。故に、NURBSモデルデータを伝送するデータ伝送系にかかる負荷は小さい。
また、ノット挿入部1401は、ノットを挿入しながら制御点列を更新し、ノット挿入部1401の最終的な出力は、入力されたNURBSモデルデータが定義するNURBS曲面の形状と完全に一致するような有理ベジエ曲面を定義する制御点列を出力する。
さらに、図示はしていないが、曲面画像処理装置100の表示部によって、3次元ポリゴンが2次元のディスプレイ上に表示される。尚、有理ベジエ制御点データが有理ベジエ曲線を定義している場合には、曲面パッチ分割処理部105は、有理ベジエ曲線を複数の線分の集合体に近似するものとする。
NURBS曲面を記述する初期ノットベクトルを(u[0], u[1], ... ,u[I+n])及び(v[0], v[1], ... , v[J+m])とする。ここでn及びmは、媒介変数u及びvに対して定義される基底関数の次数である。I及びJは、u及びv方向の制御点数である。これらのノットベクトルによって定義されるNURBS曲面が、有理ベジエ曲面に等価変換されるようにノット挿入を施し、最終的に得られるノットベクトルを(u'[0], u'[1], ... ,u'[I'+n])及び(v[0], v[1], ... , v[J'+m])とする。ここでu方向及びv方向の最終的な制御点数はI'+n+1及びJ'+m+1である。これらの制御点は、有理ベジエ曲面が定義されない不要な制御点を含んでいる。
図24は、NURBS曲面のu方向のノットベクトルにノット挿入を行い、制御点列が変化する様子を示したものである。図24の例では、u方向の次数がn=3であり、ノットベクトルの有効範囲の開始ノットu[3]について多重化を行っている。ここで仮に、u方向のノットベクトルの最初の部分(u[0], u[1], u[2], ...)について、値が全て異なり、単調増加である場合、最終的に生成されるノットベクトル(u'[0], u'[1], u'[2], ...)は以下の関係を満たす。
u[1] = u'[1]
u[2] = u'[2]
u[3] = u'[3] = u'[4] = u'[5]
最初に、値がu[3]に等しいノット〜u =u'[4]を挿入するとき、ノット挿入位置はk=3の位置であるので、係数配列は以下のようになる。
a[1] = (〜u - u[1]) / (u[4] - u[1]) = (u[3] - u[1]) / (u[4] - u[1])
a[2] = (〜u - u[2]) / (u[5] - u[2]) = (u[3] - u[2]) / (u[5] - u[2])
a[3] = (〜u - u[3]) / (u[6] - u[3]) = 0
a[4] = 0
となる。従って、生成される制御点列は
<Q'[0]> = a[0] * <Q[0]> = <Q[0]>
<Q'[1]> = (1 - a[1]) * <Q[0]> + a[1] * <Q[1]>
<Q'[2]> = (1 - a[2]) * <Q[1]> + a[2] * <Q[2]>
<Q'[3]> = (1 - a[3]) * <Q[2]> + a[3] * <Q[3]> = <Q[2]>
<Q'[4]> = (1 - a[4]) * <Q[3]> + a[4] * <Q[4]> = <Q[3]>
となる。よって、制御点<Q[1]>が消え、新しい制御点<Q'[1]>及び<Q'[2]>が生成されたことになる。但し、NURBS曲面を定義する制御点はインデックスi,jを持つ2次元配列で表されるが、ここでは説明を容易にするため、u方向の1次元のみで表現している。このように簡略化しても一般性は失われない。さらに、値がu[3]に等しいノット〜u=u'[5]を挿入するとき、ノット挿入位置はk=4であるので、係数配列は以下のようになる。
a[1] = 1
a[2] = (u[3] - u[2]) / (u[4] - u[2])
a[3] = 0
a[4] = 0
これを用いて、生成される制御点列は
<Q"[0]> = a[0] * <Q'[0]> = <Q'[0]> = <Q[0]>
<Q"[1]> = (1 - a[1]) * <Q'[0]> + a[1] * <Q'[1]> = <Q'[1]>
<Q"[2]> = (1 - a[2]) * <Q'[1]> + a[2] * <Q'[2]>
<Q"[3]> = (1 - a[3]) * <Q'[2]> + a[3] * <Q'[3]> = <Q'[2]>
<Q"[4]> = (1 - a[4]) * <Q'[3]> + a[4] * <Q'[4]> = <Q'[3]> = <Q[2]>
となる。よって、新しい制御点<Q"[2]>が生成されたことを意味する。
B[0][3](u[3]) = 1
B[0][i](u[3]) = 0 (iは3でない)
である。これを用いて、n=1について
B[1][2](u[3]) = 1
B[1][i](u[3]) = 0 (iは2でない)
である。さらにこれを用いて、n=2について
B[2][1](u[3]) = (u[4] - u[3]) / (u[4] - u[2])
B[2][2](u[3]) = (u[3] - u[2]) / (u[4] - u[2])
B[2][i](u[3]) = 0 (iは1又は2でない)
である。さらにこれを用いて、n=3について
B[3][0](u[3]) = (u[4] - u[3]) / (u[4] - u[1]) * B[2][1](u[3])
B[3][1](u[3]) = (u[3] - u[1]) / (u[4] - u[1]) * B[2][1](u[3])
+ (u[5] - u[3]) / (u[5] - u[2]) * B[2][2](u[3])
B[3][2](u[3]) = (u[3] - u[2]) / (u[5] - u[2]) * B[2][2](u[3])
B[3][i](u[3]) = 0 (iは3以上)
である。以上より、NURBS曲面の開始点は、係数配列を〜a[i] = 1 - a[i],
〜a'[i] = 1 - a'[i]とおくと、
<P(u[3])> = B[3][0](u[3]) * <Q[0]> + B[3][1](u[3]) * <Q[1]>
+ B[3][2](u[3]) * <Q[2]>
= 〜a'[2] * 〜a[1] * <Q[0]>
+ (〜a'[2] * 〜a[1] + 〜a'[2] * a[1]) * <Q[1]>
+ a'[2] * a[2] * <Q[2]>
= <Q"[2]>
となる。故に、元のNURBS曲面の開始点は、有理ベジエ曲面に変換された制御点<Q"[2]>に一致するので、2つの制御点<Q"[0]>及び<Q"[1]>は不要となる。
u[0] = u'[0]
u[1] = u'[1]
u[2] = u[3] = u'[2] = u'[3] = u'[4]
値がu[2]及びu[3]に等しいノット〜u=u'[4]を挿入するとき、ノット挿入位置はk=3の位置であるので、係数配列は以下のようになる。
a[1] = (〜u - u[1]) / (u[4] - u[1]) = (u[2] - u[1]) / (u[4] - u[1])
a[2] = (〜u - u[2]) / (u[5] - u[2]) = 0
a[3] = (〜u - u[3]) / (u[6] - u[3]) = 0
a[4] = 0
これを用いて、生成される制御点列は、
<Q'[0]> = a[0] * <Q[0]> = <Q[0]>
<Q'[1]> = (1 - a[1]) * <Q[0]> + a[1] * <Q[1]>
<Q'[2]> = (1 - a[2]) * <Q[1]> + a[2] * <Q[2]> = <Q[1]>
<Q'[3]> = (1 - a[3]) * <Q[2]> + a[3] * <Q[3]> = <Q[2]>
<Q'[4]> = (1 - a[4]) * <Q[3]> + a[4] * <Q[4]> = <Q[3]>
となる。一方、元のNURBS曲面を定義する0でない基底関数は
B[2][1](u[3]) = (u[4] - u[3]) / (u[4] - u[2]) = 1
B[3][0](u[3]) = (u[4] - u[3]) / (u[4] - u[1]) * B[2][1](u[3])
B[3][1](u[3]) = (u[3] - u[1]) / (u[4] - u[1]) * B[2][1](u[3])
であるから、一方、NURBS曲面の開始点は、
<P(u[3])> = B[3][0](u[3]) * <Q[0]> + B[3][1](u[3]) * <Q[1]>
= (1 - a[1]) * <Q[0]> + a[1] * <Q[1]>
= <Q'[1]>
となり、制御点<Q'[1]>に一致する。故に、この場合は1つの制御点<Q'[0]>のみが不要である。
u[0] = u'[0]
u[1] = u'[1]
u[2] = u'[2]
u[3] = u[4] = u'[3] = u'[4] = u'[5]
値がu[3]及びu[4]に等しいノット〜u=u'[5]を挿入するとき、ノット挿入位置はk=4の位置であるので、係数配列は以下のようになる。
a[1] = 1
a[2] = (〜u - u[2]) / (u[5] - u[2]) = (u[3] - u[2]) / (u[5] - u[2])
a[3] = (〜u - u[3]) / (u[6] - u[3]) = 0
a[4] = (〜u - u[4]) / (u[7] - u[4]) = 0
これを用いて、生成される制御点列は、
<Q'[0]> = a[0] * <Q[0]> = <Q[0]>
<Q'[1]> = (1 - a[1]) * <Q[0]> + a[1] * <Q[1]> = <Q[1]>
<Q'[2]> = (1 - a[2]) * <Q[1]> + a[2] * <Q[2]>
<Q'[3]> = (1 - a[3]) * <Q[2]> + a[3] * <Q[3]> = <Q[2]>
<Q'[4]> = (1 - a[4]) * <Q[3]> + a[4] * <Q[4]> = <Q[3]>
となる。一方、NURBS曲面の開始点を求めると、
<P(u[3])> = B[3][1](u[3]) * <Q[1]> + B[3][2](u[3]) * <Q[2]>
= (1 - a[2]) * <Q[1]> + a[2] * <Q[2]>
= <Q'[2]>
となり、制御点<Q'[2]>に一致する。故に、この場合は、2つの制御点<Q'[0]>及び<Q'[1]>は不要となる。
さて、ここで、サブディビジョン法による有理ベジエ曲面のポリゴン分割に関して説明しておく。まずは理解を容易にするために、有理ベジエ曲線について述べる。図15に示すように、有理ベジエ曲線にサブディビジョン法を適用し、複数の線分に近似する場合を考える。図15の有理ベジエ曲線は、次数n=3で、4つの制御点(Q[0],Q[1],Q[2],Q[3])で定義されている。各制御点の重みをqw[i]とする。但し、i=0、1、2、3である。図15のように、有理ベジエ曲線は制御点Q[0]及びQ[3]を両端とする曲線である。本実施例におけるサブディビジョン法では、まず2つの隣り合う制御点のちょうど中間の位置に新しい点(R[0], R[1], R[2])をとる。但し、座標計算は、位置座標に重みを乗じた同次座標を用いて以下のように行う。
rw[1] * <R[1]> = (qw[1] * <Q[1]> + qw[2] * <Q[2]>) / 2
rw[2] * <R[2]> = (qw[2] * <Q[2]> + qw[3] * <Q[3]>) / 2
但し、
rw[0] = (qw[0] + qw[1]) / 2
rw[1] = (qw[1] + qw[2]) / 2
rw[2] = (qw[2] + qw[3]) / 2
さらに、これらの中間の位置に新しい点(S[0], S[1])をとると、その座標は、
sw[0] * <S[0]> = (rw[0] * <R[0]> + rw[1] * <R[1]>) / 2
sw[1] * <S[1]> = (rw[1] * <R[1]> + rw[2] * <R[2]>) / 2
但し、
sw[0] = (rw[0] + rw[1]) / 2
sw[1] = (rw[1] + rw[2]) / 2
である。またさらに、これらの中間の位置に新しい点T[0]をとると、その座標は、
tw[0] * <T[0]> = (sw[0] * <S[0]> + sw[1] * <S[1]>) / 2
但し、
tw[0] = (sw[0] + sw[1]) / 2
である。以上のように計算を行うと、元の有理ベジエ曲線は、制御点(Q[0], R[0], S[0], T[0])からなる有理ベジェ曲線1501と、制御点(T[0], S[1], R[2], Q[3])からなる有理ベジェ曲線1502の、2つの連続な有理ベジエ曲線のセグメントに分割され、最終的な点T[0]は元の有理ベジエ曲線上の点となる。従って、元の有理ベジエ曲線は、線分(Q[0], T[0])及び線分(T[0], Q[3])の2つの線分に近似することが可能である。さらに細かい線分に分割して近似精度を向上させたい場合には、分割された有理ベジェ曲線1501及び202に対し、このサブディビジョン法を再度適用して、分割を繰り返せばよい。このように、サブディビジョン処理は乗算及び加算、「2」を用いた除算の繰り返しからなり、NURBSの基底関数を求める演算に比べて非常に単純である。
この有理ベジエ曲面に対してサブディビジョン法を適用するには、まず制御点のインデックスjの値を0に固定し、4つの制御点(Q[0][0], Q[1][0], Q[2][0], Q[3][0])を用いて前記のサブディビジョン法を適用する。これにより、制御点(Q[0][0], R[0][0], S[0][0], T[0][0])からなる有理ベジェ曲線1601と、制御点(T[0][0], S[1][0], R[2][0], Q[3][0])からなる有理ベジェ曲線1602が生成し、元の有理ベジエ曲面上の新しい点T[0][0]が求められる。図16には、この点T[0][0]のみが示されている。
(Q[0][0], Q[0][1], Q[0][2], Q[0][3])
(R[0][0], R[0][1], R[0][2], R[0][3])
(S[0][0], S[0][1], S[0][2], S[0][3])
(T[0][0], T[0][1], T[0][2], T[0][3])
(S[1][0], S[1][1], S[1][2], S[1][3])
(R[2][0], R[2][1], R[2][2], R[2][3])
(Q[3][0], Q[3][1], Q[3][2], Q[3][3])
図18のように、最初の組(Q[0][0], Q[0][1], Q[0][2], Q[0][3])に対してサブディビジョン法を適用すると、制御点(Q[0][0], Q'[0][0], Q[0][1], Q'[0][1])と(Q'[0][1], Q[0][2], Q'[0][2], Q[0][3])が得られる。ここでQ'[0][1]は元の有理ベジエ曲面上の点である。同様に、他の組にもサブディビジョン法を適用し、最終的に7×7=49個の制御点が得られ、元の有理ベジエ曲面は、4×4=16個の制御点で定義された4つの小さな有理ベジエ曲面に分割される。また、分割された各々の小さな有理ベジエ曲面の制御点のうち、角にある4つの制御点は、元の有理ベジエ曲面上の点である。すなわち、9個の有理ベジエ曲面上の点が得られることになる。図18において、これらの有理ベジエ曲面上の制御点には、○印がつけられている。これらの有理ベジエ曲面上の点を隣接するものどうし組み合わせることにより、平面ポリゴンを構成することができる。尚、さらに細かいポリゴンに分割して近似精度を向上させたい場合には、分割された有理ベジエ曲面に対して再度サブディビジョン法を適用すればよい。
次に、本発明の曲面画像処理装置100の曲面パッチ分割処理部105における処理についての説明を行う。尚、曲面パッチ分割処理部105における処理については、実施の形態5から8を用いて説明を行う。
図29は、本実施の形態5における曲面パッチ分割処理部105の機能ブロック図を示す図である。
本実施の形態5においては、曲面パッチ分割処理部105は、形状入力受付部2901、シルエットエッジ検出部2902、細分割レベル決定部2903、及び細分割部2904を備える。以下、それぞれの機能について詳細に説明する。
まず各パッチについて、シルエットエッジ検出部2902の透視変換部2902aは、視点情報に含まれている視野変換行列及び透視変換行列を用いて、制御点のうち曲面上に存在する4頂点Q00、Q30、Q03、Q33を透視変換し、スクリーン上での座標に変換する(S3102)。
S1=(r30x*r33y+r03x*r30y+r33x*r03y−r03x*r33y−r33x*r30y−r30x*r03y)/2
ここで、*は積である。スクリーン上において4頂点が図32(a)のような位置関係にある場合、符号付面積S0及びS1は同符号となるが、図32(b)の場合には異符号となる。
(2)Ap+|Am|>MAXAならば、MAXA=Ap+|Am|とする。
オブジェクトを構成する全てのパッチについて以上の処理が完了すると、S3105に移行する(S3101でY)。
そして、シルエットエッジ検出部2902は、算出された各パッチの符号付面積を参照し、正負の値がともに0でない場合(図32(b)の場合)には、そのパッチはシルエットエッジを形成しているとしてエッジ識別子を「1」にし、次のパッチの判定に移行する(S3106)。また、シルエットエッジ検出部2902は、S3106で正負どちらかの値が0の場合には、S3107に移行する。
そして、シルエットエッジ検出部2902は、当該パッチと隣接するパッチとの符号付面積の符号が異なれば(S3107でN)、その2個のパッチの間に表面と裏面の境界が存在することがわかり、シルエットエッジ形成パッチであると判定できる。従って、当該パッチと隣接する4個のパッチの符号付面積との積の値が負であればシルエットエッジ形成パッチであると判定して、エッジ識別子を「1」にする(S3108)。
ところで、曲面パッチをポリゴンの集合で近似する方法は大きく以下の2種類に大別される。
二つ目の方法では、パッチを2分割するための制御点を生成し、それを再帰的に繰り返してポリゴンを生成する方法である。前者をテッセレーションアルゴリズム、後者をサブディビジョンアルゴリズムと称す。
図34は、細分割レベル決定部2903における処理の流れを示すフローチャートである。以下、図34を参照しながらそれぞれのステップを詳細に説明する。
一方、細分割レベル決定部2903は、エッジ識別子が「0」でありシルエットエッジを形成するパッチでない場合においては(S3403でN)、そのパッチの正の符号付面積を参照して細分割レベルを決定する。なぜならば、負の符号付面積が大きい場合にはそのパッチは裏向き、すなわち視点からは見ることのできない領域が非常に大きく、分割する必要がないためである。具体的には図35(b)に示すようなテーブル3502をテーブル記憶部2903aに記録しておき、このテーブル3502を参照することで細分割レベルを決定する(S3405)。尚、図35(b)のテーブル3502において、Ai(i=0,...,4)は符号付面積の閾値である。上述した処理を全てのパッチについて完了するまで続ける(S3402)。
また、例えば、発生した隙間に新たにポリゴンを生成する方法がある。図36(a)に細分割前のオブジェクトの例を示し、図36(b)に、細分割を施した後のオブジェクトの例を示す。図36(b)の例では、オブジェクトの輪郭を生成するシルエットエッジ形成パッチはレベル2まで分割されており、その他のパッチはスクリーン上での面積に応じてレベル0又はレベル1まで分割されている。従って、シルエットエッジか否かを検出することにより、曲面画像をより精密に描画することが可能となる。
尚、本実施の形態5における曲面画像処理装置100は、パッチ上に存在する制御点のみを用いてポリゴン近似し描画する場合に特に有効である。
次に、本実施の形態6に係る曲面画像処理装置100を、図面を参照しながら説明する。尚、本実施の形態6における曲面画像処理装置100の機能構成は、上述の実施の形態5と同様であるが、シルエットエッジ検出部2902及び細分割レベル決定部2903における処理が異なる。以下、それぞれの機能について詳細に説明する。
最初に、パッチ上に存在する制御点のみを透視変換した実施の形態6と異なり、全ての制御点(4階(3次)の有理ベジェ曲面の場合は16頂点)を透視変換して(S3702)、2次元スクリーン上に変換する。ここで、隣接する制御点を結ぶと、図30に示すような2次元スクリーン上に3×3=9個の図形が生成される。以降、この生成された図形をコントロールポリゴンと称す。
そこで、シルエットエッジ検出部2902は、前述した記憶領域から加算された正負の符号付面積の値を取得して積を算出して0となるかの判定を行う(S3704)。その積が「0」でなければ(S3704でN)、シルエットエッジ形成パッチであると判定し(S3705)、エッジ識別子を「1」にする。
図39は、本実施の形態6に係る細分割レベル決定部2903における処理の流れを示すフローチャートである。
最初に、シルエットエッジ検出部2902は、エッジ識別子を参照して、各パッチがシルエットエッジ形成パッチであるか否かを調べる(S4102)。シルエットエッジ形成パッチである場合には(S4102でY)、正負の符号付面積の絶対値和に基づき、シルエットエッジ用テーブルを参照してuv方向軸の細分割レベルを決定する(S4103)。従って、シルエットエッジ形成パッチに関してはu、v軸方向が同じ細分割レベルとなる。但し、シルエットエッジ形成パッチについても後述する方法を用いて、u、v軸方向で独立に細分割レベルを決定してもよい。その場合、シルエットエッジ部分が滑らかにならない可能性があることに注意を要する。
同様に図42(c)ではv軸方向に、図42(d)ではu、v両軸方向に細かく分割する必要があることがわかる。これらの性質を利用して本手法では、u、vそれぞれの軸方向に存在するコントロールポリゴンの面積比をパッチの湾曲の程度を表す指標として用い、細分割レベルを決定する。以降、湾曲の度合いを表す指標を湾曲パラメータと称す。
また、細分割レベル決定部2903は、パッチを構成するコントロールポリゴンの符号付面積が全て負であるか否かを調べ、負でない場合においては(S4104でN)、次に、u軸方向に存在するコントロールポリゴンの面積比を算出する(S4106)。具体的には以下の手順に従う。
(2)(1)で取得された符号付面積の値をA0、A1、A2とすると、これらのうち最大値AMAXと最小値AMINを求める。
(3)以下の式を計算し、湾曲パラメータCu0を求める。
(4)Qj1、Qj2(j=0,...,3)により形成されるコントロールポリゴン、及びQj2、Qj3(j=0,...,3)により形成されるコントロールポリゴンを用いて同様の処理を行い、Cu1、Cu2をそれぞれ算出する。
(5)(3)及び(4)の値を平均して細分割レベルの決定に用いる湾曲パラメータCuを算出する。
尚、ここでは全てのコントロールポリゴンを用いて面積比を求め、その平均を湾曲パラメータとしたが、その限りではない。例えば、境界線v=0、v=1に隣接しているコントロールポリゴンのみを用いて湾曲パラメータを算出し、その平均を求めてもよい。逆に、u軸に平行な境界線に隣接しないコントロールポリゴンのみを用いて算出してもよい。
このように、本実施の形態6に係る曲面画像処理装置100によれば、各パッチを構成する全ての制御点を透視変換することでスクリーン座標系に変換し、それによって形成される全てのコントロールポリゴンの符号付面積を算出する。算出された符号付面積からシルエットエッジ形成パッチであるか否かをシルエットエッジ検出部2902において判定し、その判定結果と符号付面積の値に応じて、細分割レベル決定部2903において細分割レベルを決定する。
以下、本実施の形態7に係る曲面画像処理装置100を、図面を参照しながら説明する。 図44は、本実施の形態7における曲面画像処理装置100の構成の一例を示す図である。尚、本実施の形態7における曲面画像処理装置100は、実施の形態5で説明した手段に加えて、さらに最大細分割レベル決定部4401を備えていることを特徴とする。
方法1は、図45(a)参照するものであり、最大細分割レベル決定部4401においてパッチ上に存在する制御点によって張られる平面と、それ以外の制御点との間の距離を算出して曲率パラメータを決定する方法である。具体的には以下の手順に従う。
(2)一般に、平面α:a*x+b*y+c*z+d=0と、3次元空間上の点P(x0,y0,z0)との間の距離Lは以下の式で求められる。ここで、*は積である。
(3)制御点Q30、Q33、Q03によって張られる平面の方程式α1を求める。
(5)制御点Q03とQ30及びQ00とQ33を結ぶ対角線の長さd0、d1をそれぞれ求める。
(6)以下の式を解き、曲率パラメータCを算出する。
l1=l12'+l13'+l21'+l22'+l23'+l31'+l32'
C=(l0+l1)/(d0+d1)
尚、ここでは張られる平面に応じて距離を算出する制御点を2個のグループに分けたが、その方法は特に限定しない。例えば、それぞれの平面に対して平面上にない全ての制御点との距離を求めて曲率パラメータを決定しても良い。逆に、代表的な点(例えば、制御点の中で中央に位置するQ11、Q12、Q21、Q22)のみを用いる方法でも良い。
(1)制御点Q0iとQ3iを結ぶ線分の長さdiを算出する。
(2)u方向に隣接する制御点QjiとQ(j+1)iを結んだ線分の長さlij(j=0,...,2)を算出する。
(3)以下の式を解き、Ciを算出する。
Ci=(li0+li1+li2)/di
(4)(1)〜(3)までの処理を繰り返し、C0、C1、C2、C3を求める。
(5)制御点Qi0とQi3を結ぶ線分の長さdi'を算出する。
(6)v方向に隣接する制御点QijとQi(j+1)を結んだ線分の長さlij'(j=0,...,2)を算出する。
(7)以下の式を解き、Ci'を算出する。
Ci'=(li0'+li1'+li2')/di'
(8)(5)〜(7)までの処理を繰り返し、C0'、C1'、C2'、C3'を求める。
(9)(4)と(8)で求めた値から平均を算出し、曲率パラメータCとする。
C=(C0+C1+C2+C3+C0'+C1'+C2'+C3')/8
尚、ここでは制御点を用いて形成される全ての線分について処理を行い、曲率パラメータを決定したが、その方法は特に限定しない。例えば境界線上(u=0、u=1、v=0、v=1)についてのみ処理を行い決定しても良い。
細分割部2904では、細分割レベル決定部2903において決定された細分割レベルに応じて各パッチを細分割し、隙間を補正する処理を行う。
以下、本発明の実施の形態8に係る曲面画像処理装置100を、図面を参照しながら説明する。
オブジェクトが数個のパッチによって構成されている場合や、非常に大きなパッチばかりで構成されている場合、それらに細分割レベルを設定すると、全体的に粗くしか分割されない、或いは過度に細かく分割される可能性が高く、柔軟なレベルの制御を行うことは困難である。そこで、初期細分割部4801では、細分割レベルを決定する前に予め数レベルの細分割を実施する。細分割レベル決定部2903では、数レベル分割された後の各パッチに対して細分割レベルを決定する。初期細分割部4801における細分割レベル数を決定する方法は特に限定しない。予めレベル数を決定しておいても良いし、オブジェクトを構成するパッチの個数に応じて決定しても良い。或いは、オブジェクトを構成する初期のパッチを透視変換して符号付面積を算出し、その最小値より細分割レベルを決定しても良い。
シルエットエッジ検出部2902、細分割レベル決定部2903、細分割部2904では、初期細分割部4801において細分割された全てのパッチについて処理を行い、ポリゴン近似されたオブジェクトを生成する。 尚、本実施の形態8における曲面画像処理装置100は、最大細分割レベル決定部4401を備えていても良い。
次に、実施の形態9を用いて本発明に係る曲面画像処理装置100の法線計算部106における有理ベジェ曲面の各制御点の法線計算の処理についての説明を行う。尚、この法線計算においては、ベジェ曲面の緯度、明るさ等を決定するものである。
法線計算部106は、データ変換部105でベジェデータに変換された後のベジェ曲面の各制御頂点の座標が入力される制御頂点入力部5001、各制御頂点の法線ベクトルの算出を行う法線算出部5002、及び透視変換部107に対して制御点の出力を行う制御点出力部5003を備える。
図51は、曲面画像処理装置100の別の構成を表すブロック図であり、法線ベクトルの計算処理を実際に行うCPU5101、I/05102、ベジェ曲面の制御点の情報を記憶するメモリ5103を備える。また、メモリ5103は、図55に示すテーブル情報を記憶するテーブル記憶部5103aを保持する。
最初に、制御頂点入力部5001には、曲面パッチ分割処理部105からベジエ曲面を構成する制御点Pij(0≦i,j≦3)が入力される(S5201)。制御点の情報はI/05102を通じて、メモリ5103に記録される。尚、この制御点の情報は、上述したように、キーボードから入力しても構わず、また記録メディアに記録されたマテリアルの読み込み部を通じて入力しても構わない。
いずれの制御点とも縮退せず一致していない場合には(S5202でN)、法線算出部5002は隣接する制御点間の差分ベクトルを算出する。つまり、差分ベクトル(P10−P00)と、差分ベクトル(P01−P00)とを算出する(S5203)。
一方、法線算出部5002は、制御点であるP00とP01、P00とP10の、いずれか、或いは、両方が縮退して一致する場合には、近傍の制御点を用いて法線を算出する(S5206でY)。このように隣接する制御点が縮退している場合について、図54(a)、(b)及び(c)を用いて説明を行う。
図54(a)には、P00とP01が一致する場合の例を示している。差分ベクトル5401は(P10−P00)であり、差分ベクトル5402は(P11−P00)であり、法線ベクトル5403はこれらの外積(P10−P00)×(P11−P00)となる。
制御点出力部5003は、法線計算部106にて計算された法線の情報が入力される。或いは、メモリ203に保存する。図55(b)は、メモリ203に保存される法線データの格納例を示す。尚、図55(a)及び(b)では、制御点の頂点座標と、法線とを独立に管理している様子を示したが、一括で管理することができるのは言うまでもない。
以上の説明のように、本実施の形態9に係る法線計算部106においては、法線の計算の対象となる隣接する制御点が縮退しているような場合においても、法線算出部5002においてベジエ曲面の制御点の法線ベクトルを正しく効率的に計算することができる。尚、ベジェ曲面上にのる制御点のみを用いて3次元画像の描画処理を行う場合は、曲面内部の制御点に関する法線計算を行う必要はない。
32 制御点
33 NURBS曲面
34 制御点
41 有理ベジェ曲線
42 有理ベジェ曲線の制御点データ
43 有理ベジェ曲面パッチ
44 有理ベジェ曲面パッチの制御点データ
100 曲面画像処理装置
101 データ入力部
102 座標変換部
103 アニメーション制御部
104 データ変換部
105 曲面パッチ分割処理部
106 法線計算部
107 透視変換部
108 レンダリング処理部
1201 セグメント分配部
1202 セグメント分割部
1401 ノット挿入部
1402 制御点トリミング部
1403 有理ベジエ制御点データ決定部
1501,1502,1601,1602 分割された有理ベジエ曲線
1901,2001,2101 NURBS曲線
2201 NURBS曲面
u,v 媒介変数
u[i],u'[i] u方向のノットベクトル
v[j],v'[j] v方向のノットベクトル
Q 制御点
Q',Q" ノット挿入により生じた制御点
R,S,T サブディビジョンにより生じた制御点
〜u 挿入されたノット
2901 形状入力受付部
2902 シルエットエッジ検出部
2902a 透視変換部
2902b 符号付面積算出部
2902c リスト記憶部
2903 細分割レベル決定部
2903a テーブル記憶部
2904 細分割部
4401 最大細分割レベル決定部
4801 初期細分割部
5001 制御頂点入力部
5002 法線計算部
5002a 判定部
5003 制御点出力部
5101 CPU
5102 I/0
5103a テーブル記憶部
5103 メモリ
Claims (42)
- 3次元オブジェクトの形状データであるNURBSデータを用いて前記3次元オブジェクトを画面上に描画する曲面画像処理装置であって、
NURBS曲線及びNURBS曲面を形成する前記NURBSデータを、有理ベジェ曲線及び有理ベジェ曲面を形成する有理ベジェ制御点データにパラメータ変換するデータ変換手段と、
当該データ変換手段において変換された前記有理ベジェ制御点データから成る有理ベジェ曲面パッチを、複数の曲面パッチに細分割する曲面分割手段と、
前記曲面パッチを用いて前記3次元オブジェクトを描画する描画手段とを備え、
前記NURBSデータは制御点列とノットベクトルとからなり、
前記データ変換手段は、
ノット挿入アルゴリズムを用いてノットを前記ノットベクトルに挿入する演算を行うノット挿入部と、
当該ノット挿入部の演算により生じる制御点列に含まれる制御点の内から不要な制御点を削除する制御点トリミング部とを備える
ことを特徴とする曲面画像処理装置。 - 前記ノット挿入部は、前記NURBSデータに含まれる初期ノットベクトル及び初期制御点列から、前記有理ベジェ制御点データを表す最終ノットベクトル及び最終制御点列へと変換する過程において、前記最終ノットベクトルの特定の位置にあるノットのインデックスを探索し、
前記制御点トリミング部は、探索された前記インデックスを用いて、前記最終ノットベクトルの特定の制御点を削除する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記制御点トリミング部は、前記NURBSデータの次数が3であり、前記最終制御点列がIを整数として(Q[0], Q[1], ... ,Q[I-1])であり、前記最終ノットベクトルが(u[0], u[1], ... , u[I+3])であり、前記NURBSデータを描き始めるノットu[3]について、(u[j], ... , u[3], ..., u[k])の(k−j+1)個のノットの値がu[3]に等しく多重度3以上で多重化されているとき、前記最終制御点列のうち(Q[0], Q[1], ... ,Q[k-4])の(k−3)個の制御点を削除する
ことを特徴とする請求項2記載の曲面画像処理装置。 - 前記制御点トリミング部は、前記NURBSデータの次数が3であり、前記最終制御点列がIを整数として(Q[0], ... , Q[I-2], Q[I-1])であり、前記最終ノットベクトルが(u[0], ... , u[I+2], u[I+3])であり、前記NURBSデータが描き終わるノットu[I]について、(u[j], ... , u[I], ..., u[k])の(k−j+1)個のノットの値がu[I]に等しく多重度3以上で多重化されているとき、前記最終制御点列のうち(Q[j], ... , Q[I-2], Q[I-1])の(I−j)個の制御点を削除する
ことを特徴とする請求項2記載の曲面画像処理装置。 - 前記制御点列を構成する各制御点は、重みを有し、
前記ノット挿入部は、前記制御点列を同次座標系において操作する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記ノット挿入部は、前記ノットベクトルの特定の範囲にある各々の要素に対し、特定の多重度で多重化されるように、ノットを挿入する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面画像処理装置は、さらに、
前記NURBSデータに座標変換を施し、前記3次元オブジェクトの視点情報を用いて視野座標系におけるNURBSデータに変換する座標変換手段を備える
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記座標変換手段は、さらに、前記有理ベジェ制御点データに座標変換を施し、前記視点情報を用いて視野座標系における有理ベジェ制御点データに変換する
ことを特徴とする請求項7記載の曲面画像処理装置。 - 前記NURBSデータ及び前記有理ベジェ制御点データは、同次座標系で扱われる
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面分割手段は、前記有理ベジェ曲面パッチを形成する前記有理ベジェ制御点データに対し、射影空間におけるド・カステリョのアルゴリズムを用いて、
(2のn乗分の1):(1−(2のn乗分の1))の比(但し、nは正整数)で内分する内分点を用いた線形補間を繰り返し適用し、新たな有理ベジェ制御点データを算出すると共に、当該新たな有理ベジェ制御点データを用いて前記有理ベジェ曲面パッチを分割する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面分割手段は、1つのn次有理ベジェ曲線を形成する有理ベジェ制御点データから分割される2つのn次有理ベジェ曲線を形成する有理ベジェ制御点データを算出する分割処理部を少なくとも1つ以上備える
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面パッチはポリゴンデータであり、
前記描画手段は、複数の前記ポリゴンデータを画素データに変換して前記3次元オブジェクトを描画する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面分割手段は、さらに、
前記オブジェクトを構成する各曲面パッチの形状を定義する前記有理ベジェ制御点データを用いて透視変換することにより構成される2次元図形の符号付面積を算出する面積算出部と、
前記曲面パッチが前記オブジェクトの輪郭部であるシルエットエッジを形成する曲面パッチであるか否かを前記符号付面積の値に基づいて検出する検出部とを備える
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記曲面分割手段は、さらに、
前記検出部において前記シルエットエッジを形成する曲面パッチであるか否かを検出した結果と、前記面積算出部で算出される前記曲面パッチのスクリーン上での前記符号付面積の値とに応じて前記曲面パッチの細分割レベルを決定する細分割レベル決定部を備える
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記細分割レベル決定部は、さらに、前記面積算出部で算出される符号付面積の最大値を特定し、特定された前記符号付面積の最大値に基づき前記シルエットエッジを形成する曲面パッチの前記細分割レベルを決定する
ことを特徴とする請求項14記載の曲面画像処理装置。 - 前記面積算出部は、さらに、オブジェクトを構成する各曲面パッチの形状を定義する全ての制御点を透視変換することにより構成される各々の2次元図形の符号付面積を算出し、
前記細分割レベル決定部は、前記面積算出部で算出された前記曲面パッチの2次元図形の前記符号付面積の値の絶対値の和に基づき、前記シルエットエッジを形成する曲面パッチの前記細分割レベルを決定する
ことを特徴とする請求項14記載の曲面画像処理装置。 - 前記細分割レベル決定部は、オブジェクトを構成する各曲面パッチを定義する第1軸及び第2軸に対してそれぞれ独立に細分割レベルを決定する
ことを特徴とする請求項14記載の曲面画像処理装置。 - 前記面積算出部は、さらに、オブジェクトを構成する各曲面パッチの形状を定義する全ての制御点を透視変換することにより構成される2次元図形のうち、第1軸方向及び第2軸方向に隣接する前記2次元図形を参照し、参照された前記2次元図形の符号付面積をそれぞれ算出し、
前記細分割レベル決定部は、算出された第1軸方向に隣接する前記2次元図形の前記符号付面積の最大値と最小値の比に応じて、第1軸方向の細分割レベルを決定すると共に、算出された第2軸方向に隣接する前記2次元図形の前記符号付面積の最大値と最小値の比に応じて、第2軸方向の細分割レベルを決定する
ことを特徴とする請求項17記載の曲面画像処理装置。 - 前記曲面分割手段は、さらに、
前記細分割レベル決定部においてオブジェクトを構成する各曲面パッチの細分割レベルを決定する前に、1レベル以上の細分割を実施する初期細分割部を備える
ことを特徴とする請求項14記載の曲面画像処理装置。 - 前記細分割レベル決定部において決定される前記細分割レベルは、サブディビジョンアルゴリズムを用いてオブジェクトを構成する各曲面パッチを第1軸及び第2軸の方向に1回ずつ細分割する操作を1レベルとするか、もしくは前記第1軸又は前記第2軸いずれかの方向に1回細分割する操作を1レベルとし、前記細分割レベルは、前記細分割する操作の回数である
ことを特徴とする請求項14記載の曲面画像処理装置。 - 前記面積算出部は、前記有理ベジェ制御点データのうち、パッチ上に存在する有理ベジェ制御点を透視変換することにより構成される2次元図形の符号付面積を算出し、
前記検出部は、当該符号付面積を用いてシルエットエッジを形成する曲面パッチであるか否かを検出する
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記検出部は、さらに、第1曲面パッチについて算出された前記2次元図形の前記符号付面積の正負の符号と、前記第1曲面パッチに隣接する曲面パッチについて算出された前記2次元図形の前記符号付面積の正負の符号とを比較し、異符号であれば当該曲面パッチはシルエットエッジを形成する曲面パッチであると検出する
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記検出部は、前記オブジェクトを構成する各曲面パッチの形状を定義する全ての制御点を透視変換することにより構成される2次元図形の符号付面積を指標として用いて、シルエットエッジを形成する曲面パッチであるか否かを判定する
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記面積算出部は、さらに、オブジェクトを構成する各曲面パッチの形状を定義する全ての制御点を透視変換することにより構成される各々の2次元図形の符号付面積を算出した後、さらに、その正負の符号別の面積の総和を算出し、
前記検出部は、前記面積算出部で算出された前記正負の符号別の総和のどちらかが0となる場合であればシルエットエッジを形成する曲面パッチではないと検出する
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記曲面分割手段は、さらに、
オブジェクトを構成する各曲面パッチの最大となる細分割レベルを予め決定する最大細分割レベル決定部を備える
ことを特徴とする請求項13記載の曲面画像処理装置。 - 前記最大細分割レベル決定部は、オブジェクトを構成する各曲面パッチの形状を定義する制御点のうち、前記曲面パッチ上に存在する前記制御点によって張られる平面と前記曲面パッチ上に存在しない前記制御点の間の距離と、前記曲面パッチ上に存在する前記制御点を結んだ対角線の長さの比に応じて、前記各曲面パッチの最大となる細分割レベルを決定する
ことを特徴とする請求項25記載の曲面画像処理装置。 - 前記最大細分割レベル決定部は、オブジェクトを構成する各曲面パッチの形状を定義する制御点のうち、前記曲面パッチ上に存在する前記制御点を結んだ線分の長さを算出し、前記曲面パッチ上に存在する前記制御点の間に存在する前記制御点について、隣接する前記制御点間の距離の和を算出し、算出された前記距離の和と前記線分の長さの比に応じて、前記各曲面パッチの前記最大細分割レベルを決定する
ことを特徴とする請求項25記載の曲面画像処理装置。 - 前記オブジェクトを構成する前記曲面パッチは有理ベジェ曲面である
ことを特徴とする請求項13から請求項27のいずれか1項に記載の曲面画像処理装置。 - 前記曲面画像処理装置は、さらに、
前記有理ベジェ曲面の前記有理ベジェ制御点を用いて各制御点の法線を算出する法線算出手段を備え、
前記法線算出手段は、前記曲面パッチの四隅である第1制御点から第4制御点における法線算出の際に、4隅の制御点の1つを順に選択し、前記選択した制御点に対して隣接する二つの制御点を選択する選択部と、
前記選択した制御点と、前記隣接する2つの制御点との間の差分ベクトルをそれぞれ算出し、算出された2つの前記差分ベクトルの外積を算出し、正規化したものを、前記選択した制御点の法線として算出する算出部とを備え、前記曲面パッチの四隅の制御点全てに対して法線を算出する
ことを特徴とする請求項1記載の曲面画像処理装置。 - 前記選択部は、前記ベジェ曲面の四隅の第1制御点から第4制御点における法線算出の際に、前記選択した制御点に対して隣接する2つの制御点のうち少なくとも一つが前記選択した制御点と縮退して同じ座標となる場合においては、法線計算の対象となる選択した制御点あるいは前記2つの制御点に対して隣接し、且つ前記選択した制御点の座標と同じとならない二つの制御点を選択し、
前記算出部は、前記選択した制御点と、前記選択部において選択される2つの制御点との間の差分ベクトルをそれぞれ算出し、2つの前記差分ベクトルの外積を算出し、正規化したものを、前記選択した制御点の法線として算出する
ことを特徴とする請求項29記載の曲面画像処理装置。 - 前記選択部は、前記ベジェ曲面の四隅の第1制御点から第4制御点における法線算出の際に、法線計算の対象となる前記選択した制御点に対して隣接している制御点が縮退している場合には、さらに当該制御点に隣接していて縮退していない制御点を選択する
ことを特徴とする請求項29記載の曲面画像処理装置。 - 前記選択部は、前記算出部において算出される2つの差分ベクトルのなす角度が所定角度以下の場合においては、さらに他の制御点を選択する
ことを特徴とする請求項29記載の曲面画像処理装置。 - 前記選択部は、法線計算の対象となる前記選択した制御点と所定距離以下の制御点を選択しない
ことを特徴とする請求項29記載の曲面画像処理装置。 - 前記選択部は、前記ベジェ曲面の四隅の制御点における法線算出の際に、四隅の制御点の一つ(P00)に対して隣接する二つの制御点(P01、P10)を選択し、
前記算出部は、P00とP01とP10とが異なる場合には、前記選択した制御点(P00)に対して隣接する二つの制御点(P01、P10)と前記選択した制御点P00との間の差分ベクトルをそれぞれ算出し、2つの前記差分ベクトルの外積を算出し、正規化したものを、前記制御点の法線として算出し、
前記選択部は、前記選択した制御点P00とこれに隣接する二つの制御点P01、P10のうち少なくとも一つが同じ座標となる場合には、近傍の縮退していない制御点を選択し、
前記算出部は、前記選択した制御点と近傍の制御点との間の差分ベクトル、及び前記選択した制御点と前記二つの制御点P01、P10のうち縮退していない制御点との間の差分ベクトルを算出し、算出された2つの前記差分ベクトルの外積を算出し、正規化したものを、前記選択した制御点の法線として算出する
ことを特徴とする請求項29記載の曲面画像処理装置。 - 3次元オブジェクトの形状データであるNURBSデータを用いて前記3次元オブジェクトを画面上に描画する曲面画像処理装置による曲面画像処理方法であって、
前記曲面画像処理装置が備えるデータ変換手段が、NURBS曲線及びNURBS曲面から形成される前記NURBSデータを、有理ベジェ曲線及び有理ベジェ曲面を形成する有理ベジェ制御点データにパラメータ変換するデータ変換ステップと、
前記曲面画像処理装置が備える曲面分割手段が、当該データ変換ステップにおいて変換された前記有理ベジェ制御点データから成る有理ベジェ曲面パッチを、複数の曲面パッチに細分割する曲面分割ステップと、
前記曲面画像処理装置が備える描画手段が、前記曲面パッチを用いて前記3次元オブジェクトを描画する描画ステップとを含み、
前記NURBSデータは制御点列とノットベクトルとからなり、
前記データ変換ステップは、
前記データ変換手段が備えるノット挿入部が、ノット挿入アルゴリズムを用いてノットを前記ノットベクトルに挿入する演算を行うノット挿入ステップと、
前記データ変換手段が備える制御点トリミング部が、当該ノット挿入ステップにおける演算により生じる制御点列に含まれる制御点の内から不要な制御点を削除する制御点トリミングステップとを含む
ことを特徴とする曲面画像処理方法。 - 前記曲面分割ステップには、さらに、
前記曲面分割手段が備える面積算出部が、前記オブジェクトを構成する各曲面パッチの形状を定義する前記有理ベジェ制御点データを用いて透視変換することにより構成される2次元図形の符号付面積を算出する面積算出ステップと、
前記曲面分割手段が備える検出部が、前記曲面パッチが前記オブジェクトの輪郭部であるシルエットエッジを形成する曲面パッチであるか否かを前記符号付面積の値に基づいて検出する検出ステップとを含む
ことを特徴とする請求項35記載の曲面画像処理方法。 - 前記曲面分割ステップには、さらに、
前記曲面分割手段が備える細分割レベル決定部が、前記検出ステップにおいて前記シルエットエッジを形成する曲面パッチであるか否かを検出した結果と、前記面積算出ステップにおいて算出される前記曲面パッチのスクリーン上での前記符号付面積の値とに応じて前記曲面パッチの細分割レベルを決定する細分割レベル決定ステップを含む
ことを特徴とする請求項36記載の曲面画像処理方法。 - 前記曲面画像処理方法は、さらに、
前記曲面画像処理装置が備える法線算出手段が、前記有理ベジェ曲面の前記有理ベジェ制御点を用いて各制御点の法線を算出する法線算出ステップを含み、
前記法線算出ステップは、
前記法線算出手段が備える選択部が、前記曲面パッチの四隅である第1制御点から第4制御点における法線算出の際に、前記曲面パッチの4隅の制御点の1つを順に選択し、前記選択した制御点に対して隣接する二つの制御点を選択する選択ステップと、
前記法線算出手段が備える算出部が、前記選択した制御点と、前記隣接する2つの制御点との間の差分ベクトルをそれぞれ算出し、算出された2つの前記差分ベクトルの外積を算出し、正規化したものを、前記選択した制御点の法線として算出し、前記曲面パッチの4隅の制御点全てに対して法線を算出する算出ステップとを含み、前記曲面パッチの四隅の制御点全てに対して法線を算出する
ことを特徴とする請求項35記載の曲面画像処理方法。 - 請求項35に記載の曲面画像処理方法に含まれる全てのステップをコンピュータに実行させる
ことを特徴とするプログラム。 - 前記曲面分割ステップでは、さらに、
前記オブジェクトを構成する各曲面パッチの形状を定義する前記有理ベジェ制御点データを用いて透視変換することにより構成される2次元図形の符号付面積を算出する面積算出ステップと、
前記曲面パッチが前記オブジェクトの輪郭部であるシルエットエッジを形成する曲面パッチであるか否かを前記符号付面積の値に基づいて検出する検出ステップとをコンピュータに実行させる
ことを特徴とする請求項39記載のプログラム。 - 前記曲面分割ステップでは、さらに、
前記検出ステップにおいて前記シルエットエッジを形成する曲面パッチであるか否かを検出した結果と、前記面積算出ステップにおいて算出される前記曲面パッチのスクリーン上での前記符号付面積の値とに応じて前記曲面パッチの細分割レベルを決定する細分割レベル決定ステップをコンピュータに実行させる
ことを特徴とする請求項40記載のプログラム。 - 前記プログラムは、さらに、
前記有理ベジェ曲面の前記有理ベジェ制御点を用いて各制御点の法線を算出する法線算出ステップをコンピュータに実行させ、
前記法線算出ステップでは、前記曲面パッチの四隅である第1制御点から第4制御点における法線算出の際に、前記曲面パッチの4隅の制御点の1つを順に選択し、前記選択した制御点に対して隣接する二つの制御点を選択する選択ステップと、
前記選択した制御点と、前記隣接する2つの制御点との間の差分ベクトルをそれぞれ算出し、算出された2つの前記差分ベクトルの外積を算出し、正規化したものを、前記選択した制御点の法線として算出し、前記曲面パッチの4隅の制御点全てに対して法線を算出する算出ステップとをコンピュータに実行させ、前記曲面パッチの四隅の制御点全てに対して法線を算出する
ことを特徴とする請求項39記載のプログラム。
Priority Applications (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2003380341A JP4464657B2 (ja) | 2002-11-12 | 2003-11-10 | 曲面画像処理装置及び曲面画像処理方法 |
| CNB2003101143697A CN100341031C (zh) | 2002-11-12 | 2003-11-12 | 曲面图像处理装置及曲面图像处理方法 |
Applications Claiming Priority (5)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| JP2002328052 | 2002-11-12 | ||
| JP2002329441 | 2002-11-13 | ||
| JP2002329443 | 2002-11-13 | ||
| JP2002329442 | 2002-11-13 | ||
| JP2003380341A JP4464657B2 (ja) | 2002-11-12 | 2003-11-10 | 曲面画像処理装置及び曲面画像処理方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| JP2004178576A JP2004178576A (ja) | 2004-06-24 |
| JP4464657B2 true JP4464657B2 (ja) | 2010-05-19 |
Family
ID=32719582
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| JP2003380341A Expired - Fee Related JP4464657B2 (ja) | 2002-11-12 | 2003-11-10 | 曲面画像処理装置及び曲面画像処理方法 |
Country Status (2)
| Country | Link |
|---|---|
| JP (1) | JP4464657B2 (ja) |
| CN (1) | CN100341031C (ja) |
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US10297072B2 (en) | 2014-12-15 | 2019-05-21 | Samsung Electronics Co., Ltd. | 3D rendering method and apparatus |
Families Citing this family (23)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US7038697B2 (en) * | 2003-02-25 | 2006-05-02 | Microsoft Corporation | Color gradient paths |
| US7646384B2 (en) * | 2005-03-31 | 2010-01-12 | Siemens Product Lifecycle Management Software Inc. | System and method to determine a simplified representation of a model |
| CN101441781B (zh) * | 2007-11-23 | 2011-02-02 | 鸿富锦精密工业(深圳)有限公司 | 曲面翻面方法 |
| US8643644B2 (en) * | 2008-03-20 | 2014-02-04 | Qualcomm Incorporated | Multi-stage tessellation for graphics rendering |
| CN101867703B (zh) * | 2009-04-16 | 2012-10-03 | 辉达公司 | 用于校正图像的系统和方法 |
| CN101692257B (zh) * | 2009-09-25 | 2012-05-16 | 华东理工大学 | 一种复杂曲面的配准方法 |
| JP4955075B2 (ja) * | 2010-01-20 | 2012-06-20 | 本田技研工業株式会社 | 設計支援システムおよび設計支援プログラム |
| CN102609987B (zh) * | 2012-01-09 | 2014-12-17 | 北京电子科技学院 | 一种通过计算零维三角多项式系统所有实根及其重数进行曲面绘制的方法和系统 |
| US9558573B2 (en) | 2012-12-17 | 2017-01-31 | Nvidia Corporation | Optimizing triangle topology for path rendering |
| CN105376555A (zh) * | 2015-12-11 | 2016-03-02 | 重庆环漫科技有限公司 | 一种立体融合播放方法 |
| CN105631817A (zh) * | 2015-12-23 | 2016-06-01 | 王蕾 | 细分有理曲面(正向)去像素化技术 |
| CN105676290B (zh) * | 2016-04-03 | 2017-10-13 | 北京工业大学 | 基于曲面细分的地震数据三维显示方法 |
| JP6782108B2 (ja) * | 2016-07-19 | 2020-11-11 | 大成建設株式会社 | 可視率算出装置 |
| EP3510483B1 (en) * | 2016-09-23 | 2023-12-20 | Huawei Technologies Co., Ltd. | Binary image differential patching |
| CN108399942A (zh) * | 2018-03-16 | 2018-08-14 | 青岛海信医疗设备股份有限公司 | 三维虚拟器官的显示方法、装置、存储介质及设备 |
| CN108428230B (zh) * | 2018-03-16 | 2020-06-16 | 青岛海信医疗设备股份有限公司 | 三维虚拟器官中处理曲面的方法、装置、存储介质及设备 |
| CN108763668B (zh) * | 2018-05-15 | 2022-03-01 | 杭州电子科技大学 | 基于细分技术与边界替换的齿轮模型区域参数化方法 |
| KR102115945B1 (ko) * | 2019-11-26 | 2020-05-27 | 성균관대학교 산학협력단 | 쿼드 메쉬를 이용해, 터널형 도로의 형상 정보를 추출하는 방법, 이를 저장하는 컴퓨터 판독가능 기록 매체, 및 이 매체에 저장되는 컴퓨터 프로그램 |
| CN111443864B (zh) * | 2020-04-14 | 2023-03-07 | 重庆赋比兴科技有限公司 | 基于iOS的曲线绘制方法 |
| CN113345065B (zh) * | 2021-08-04 | 2021-11-12 | 康达洲际医疗器械有限公司 | 一种基于指向性线段的曲面图像构建方法与系统 |
| CN116984266B (zh) * | 2023-09-26 | 2024-01-16 | 中江立江电子有限公司 | 一种连接器分拣装置及分拣方法 |
| CN117726710B (zh) * | 2024-02-18 | 2024-06-04 | 粤港澳大湾区数字经济研究院(福田) | 一种基于曲线离散的绘制方法及相关装置 |
| CN118797757B (zh) * | 2024-09-12 | 2024-12-06 | 唯实先端智能科技(苏州)有限公司 | 半导体Stocker设备洁净度气密性的提高方法 |
Family Cites Families (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| JP3926866B2 (ja) * | 1996-05-10 | 2007-06-06 | 株式会社ソニー・コンピュータエンタテインメント | 情報処理装置、情報処理方法、及び描画システム |
| JP3705923B2 (ja) * | 1998-04-09 | 2005-10-12 | 株式会社ソニー・コンピュータエンタテインメント | 画像処理装置および画像処理方法、プログラム提供媒体、並びにデータ提供媒体 |
-
2003
- 2003-11-10 JP JP2003380341A patent/JP4464657B2/ja not_active Expired - Fee Related
- 2003-11-12 CN CNB2003101143697A patent/CN100341031C/zh not_active Expired - Fee Related
Cited By (1)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US10297072B2 (en) | 2014-12-15 | 2019-05-21 | Samsung Electronics Co., Ltd. | 3D rendering method and apparatus |
Also Published As
| Publication number | Publication date |
|---|---|
| CN1499447A (zh) | 2004-05-26 |
| CN100341031C (zh) | 2007-10-03 |
| JP2004178576A (ja) | 2004-06-24 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| JP4464657B2 (ja) | 曲面画像処理装置及び曲面画像処理方法 | |
| EP1420368A2 (en) | Apparatus and method for rendering a curved surface using NURBS | |
| US5903273A (en) | Apparatus and method for generating an image for 3-dimensional computer graphics | |
| US9972129B2 (en) | Compression of a three-dimensional modeled object | |
| US8289323B2 (en) | Drawing processing apparatus, texture processing apparatus, and tessellation method | |
| Steinbrücker et al. | Volumetric 3D mapping in real-time on a CPU | |
| US5337404A (en) | Process and system for making computer-aided drawings using a contour inclusion tree associated planar map data structure | |
| JP5124615B2 (ja) | サーフェス法線ベクトルを求めるための装置又は方法 | |
| US8537158B2 (en) | Parallel triangle tessellation | |
| US8368714B2 (en) | Curved surface rendering system and method | |
| CN106251384B (zh) | 使用三角形的递归再分的细分方法 | |
| EP1011078A1 (en) | Method for generating polygon data and image display using the same | |
| Ruprecht et al. | Spatial free-form deformation with scattered data interpolation methods | |
| CN109035407B (zh) | 基于方向的参数曲面三角化方法、装置、设备及存储介质 | |
| US9779528B2 (en) | Text realization | |
| US7388584B2 (en) | Method and program for determining insides and outsides of boundaries | |
| US7015917B2 (en) | Curved surface subdivision apparatus | |
| Schollmeyer et al. | Efficient and anti-aliased trimming for rendering large NURBS models | |
| Melançon | Living flows: enhanced exploration of edge-bundled graphs based on GPU-intensive edge rendering | |
| JP2004102841A (ja) | クリッピング処理装置、グラフィックスシステム、クリッピング処理方法及びグラフィックス方法 | |
| KR100392516B1 (ko) | 보간되지 않은 볼륨 데이터의 실시간 렌더링 방법 | |
| JP4479957B2 (ja) | 曲面細分割装置 | |
| CN117893655B (zh) | 一种提升裁剪点搜索速度和gpu速度的方法 | |
| JP5504142B2 (ja) | 画像処理装置、画像処理方法及び画像処理プログラム | |
| JPH0887585A (ja) | 図形データの階層的近似化方法 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| A621 | Written request for application examination |
Free format text: JAPANESE INTERMEDIATE CODE: A621 Effective date: 20060828 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20090721 |
|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20090916 |
|
| A131 | Notification of reasons for refusal |
Free format text: JAPANESE INTERMEDIATE CODE: A131 Effective date: 20091110 |
|
| A521 | Written amendment |
Free format text: JAPANESE INTERMEDIATE CODE: A523 Effective date: 20091217 |
|
| TRDD | Decision of grant or rejection written | ||
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 Effective date: 20100126 |
|
| A01 | Written decision to grant a patent or to grant a registration (utility model) |
Free format text: JAPANESE INTERMEDIATE CODE: A01 |
|
| A61 | First payment of annual fees (during grant procedure) |
Free format text: JAPANESE INTERMEDIATE CODE: A61 Effective date: 20100219 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20130226 Year of fee payment: 3 |
|
| R150 | Certificate of patent or registration of utility model |
Ref document number: 4464657 Country of ref document: JP Free format text: JAPANESE INTERMEDIATE CODE: R150 Free format text: JAPANESE INTERMEDIATE CODE: R150 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20130226 Year of fee payment: 3 |
|
| FPAY | Renewal fee payment (event date is renewal date of database) |
Free format text: PAYMENT UNTIL: 20140226 Year of fee payment: 4 |
|
| LAPS | Cancellation because of no payment of annual fees |