A roulette is a curve traced by a fixed point on a closed convex curve as that curve rolls without slipping along a second curve. The roulettes described by the foci of conics when rolled upon a line are sections of minimal surfaces (i.e., they yield minimal surfaces when revolved about the line) known as unduloids.
|

|
|

|
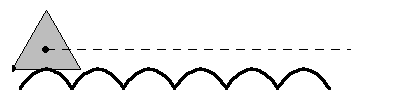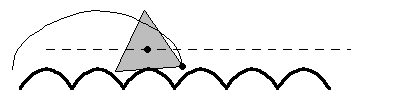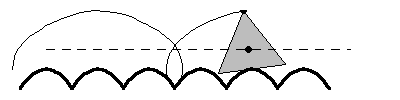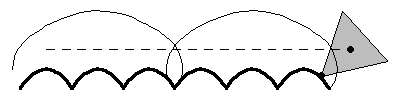
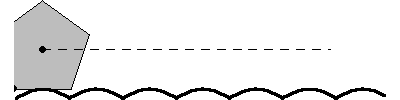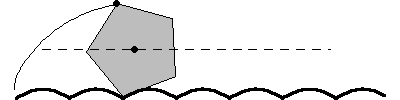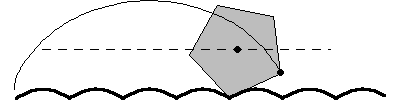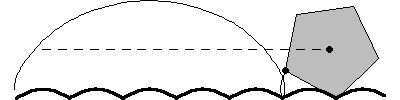
A particularly interesting case of a roulette is a regular -gon rolling on a "road" composed of a sequence of
truncated catenaries, as illustrated above, as first
noted by Robison (1960). This motion is smooth in the sense that the geometric
centroid follows a straight line, although in the case of the rolling equilateral
triangle, a physical model would be impossible to construct because the vertices
of the triangles would get "stuck" in the ruts (Wagon 2000). For the rolling
square (a "square wheel"), the shape of the
road is the catenary
truncated at
(Wagon 2000). Interestingly, a detailed mathematical
analysis had been published by J. C. Maxwell (of electromagnetic theory
fame) in 1849 (Maxwell 1849) which, while its did not include critical idea of truncating
catenaries, contained essentially all the other underlying mathematical ideas.
For a regular -gon,
the Cartesian equation of the corresponding catenary
is
where

The roulette consisting of a square on a truncated catenary road is depicted on the cover of Wagon (2000).
Given a base curve, let another curve roll on it, and call the point rigidly attached to this rolling curve the "pole." The following table then summarizes some roulettes for various common curves and poles. Note that the cases curtate cycloid, cycloid, and prolate cycloid are together called trochoids, and similarly for the various varieties of epicycloids (called epitrochoids) and hypocycloids (called hypotrochoids).
| base curve | rolling curve | pole | roulette |
| any curve | line | on line | involute of the curve |
| circle | exterior circle of radius | curtate epicycloid | |
| circle | exterior circle of radius | epicycloid | |
| circle | exterior
circle of radius | prolate epicycloid | |
| circle | interior circle of radius | curtate hypocycloid | |
| circle | interior circle of radius | hypocycloid | |
| circle | interior
circle of radius | prolate hypocycloid | |
| circle | exterior equal circle | any point | rose curve |
| line | circle
of radius | curtate cycloid | |
| line | circle of radius | cycloid | |
| line | circle
of radius | prolate cycloid | |
| line | circle involute | center | parabola |
| line | cycloid | center | ellipse |
| line | ellipse | focus | elliptic catenary |
| line | hyperbola | focus | hyperbolic catenary |
| line | hyperbolic spiral | origin | tractrix |
| line | logarithmic spiral | any point | line |
| line | parabola | focus | catenary |
| parabola | equal parabola | parabola vertex | cissoid of Diocles |