Ellipse

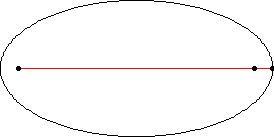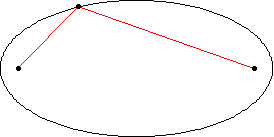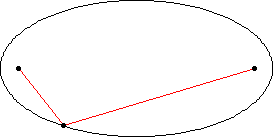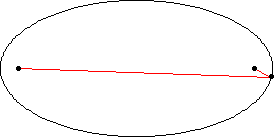
An ellipse is a curve that is the locus of all points in the plane the sum of whose distances and from two fixed points and (the foci) separated by a distance of is a given positive constant (Hilbert and Cohn-Vossen 1999, p. 2). This results in the two-center bipolar coordinate equation

where is the semimajor axis and the origin of the coordinate system is at one of the foci. The corresponding parameter is known as the semiminor axis.

The ellipse is a conic section and a Lissajous curve.

An ellipse can be specified in the Wolfram Language using Circle[x, y, a, b].

If the endpoints of a segment are moved along two intersecting lines, a fixed point on the segment (or on the line that prolongs it) describes an arc of an ellipse. This is known as the trammel construction of an ellipse (Eves 1965, p. 177).

It is possible to construct elliptical gears that rotate smoothly against one another (Brown 1871, pp. 14-15; Reuleaux and Kennedy 1876, p. 70; Clark and Downward 1930; KMODDL).

The ellipse was first studied by Menaechmus, investigated by Euclid, and named by Apollonius. The focus and conic section directrix of an ellipse were considered by Pappus. In 1602, Kepler believed that the orbit of Mars was oval; he later discovered that it was an ellipse with the Sun at one focus. In fact, Kepler introduced the word "focus" and published his discovery in 1609. In 1705 Halley showed that the comet now named after him moved in an elliptical orbit around the Sun (MacTutor Archive). An ellipse rotated about its minor axis gives an oblate spheroid, while an ellipse rotated about its major axis gives a prolate spheroid.

A ray of light passing through a focus will pass through the other focus after a single bounce (Hilbert and Cohn-Vossen 1999, p. 3). Reflections not passing through a focus will be tangent to a confocal hyperbola or ellipse, depending on whether the ray passes between the foci or not.

Let an ellipse lie along the x-axis and find the equation of the figure (1) where and are at and . In Cartesian coordinates,

Bring the second term to the right side and square both sides,

Now solve for the square root term and simplify

Square one final time to clear the remaining square root,

Grouping the terms then gives

which can be written in the simple form

Defining a new constant

puts the equation in the particularly simple form

The parameter is called the semiminor axis by analogy with the parameter , which is called the semimajor axis (assuming ). The fact that as defined above is actually the semiminor axis is easily shown by letting and be equal. Then two right triangles are produced, each with hypotenuse , base , and height . Since the largest distance along the minor axis will be achieved at this point, is indeed the semiminor axis.

If, instead of being centered at (0, 0), the center of the ellipse is at (, ), equation (◇) becomes

As can be seen from the Cartesian equation for the ellipse, the curve can also be given by a simple parametric form analogous to that of a circle, but with the and coordinates having different scalings,

The general quadratic curve

is an ellipse when, after defining

, , and . Also assume the ellipse is nondegenerate (i.e., it is not a circle, so , and we have already established is not a point, since ). In that case, the center of the ellipse is given by

the semi-axis lengths are

and the counterclockwise angle of rotation from the -axis to the major axis of the ellipse is

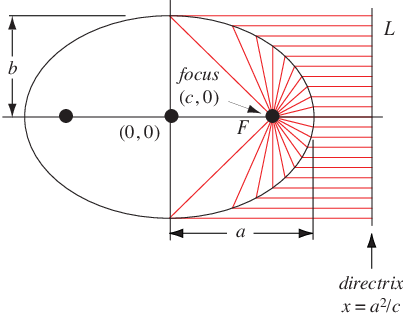
The ellipse can also be defined as the locus of points whose distance from the focus is proportional to the horizontal distance from a vertical line known as the conic section directrix, where the ratio is . Letting be the ratio and the distance from the center at which the directrix lies, then in order for this to be true, it must hold at the extremes of the major and minor axes, so

Solving gives

The focal parameter of the ellipse is

where is a characteristic of the ellipse known as the eccentricity, to be defined shortly.

An ellipse whose axes are parallel to the coordinate axes is uniquely determined by any four non-concyclic points on it, and the ellipse passing through the four points , , , and has equation

Let four points on an ellipse with axes parallel to the coordinate axes have angular coordinates for , 2, 3, and 4. Such points are concyclic when

where the intermediate variable has been defined (Berger et al. 1984; Trott 2006, pp. 39-40). Rather surprisingly, this same relationship results after simplification of the above where is now interpreted as . An equivalent, but more complicated, condition is given by

Like hyperbolas, noncircular ellipses have two distinct foci and two associated directrices, each conic section directrix being perpendicular to the line joining the two foci (Eves 1965, p. 275).

Define a new constant called the eccentricity (where is the case of a circle) to replace

from which it follows that

The eccentricity can therefore be interpreted as the position of the focus as a fraction of the semimajor axis.

If and are measured from a focus instead of from the center (as they commonly are in orbital mechanics) then the equations of the ellipse are

and (◇) becomes

Clearing the denominators gives

Substituting in gives

Plugging in to re-express and in terms of and ,

Dividing by and simplifying gives

which can be solved for to obtain

The sign can be determined by requiring that must be positive. When , (47) becomes , but since is always positive, we must take the negative sign, so (47) becomes

The distance from a focus to a point with horizontal coordinate (where the origin is taken to lie at the center of the ellipse) is found from

Plugging this into (50) yields

In pedal coordinates with the pedal point at the focus, the equation of the ellipse is

The arc length of the ellipse is

where is an incomplete elliptic integral of the second kind with elliptic modulus (the eccentricity).

The relationship between the polar angle from the ellipse center and the parameter follows from

This function is illustrated above with shown as the solid curve and as the dashed, with . Care must be taken to make sure that the correct branch of the inverse tangent function is used. As can be seen, weaves back and forth around , with crossings occurring at multiples of . The curvature and tangential angle of the ellipse are given by

The entire perimeter of the ellipse is given by setting (corresponding to ), which is equivalent to four times the length of one of the ellipse's quadrants,

where is a complete elliptic integral of the second kind with elliptic modulus (the eccentricity). The perimeter can be computed using the rapidly converging Gauss-Kummer series as

(OEIS A056981 and A056982), where is a binomial coefficient and

This can also be written analytically as

where is a hypergeometric function, is a complete elliptic integral of the first kind.

Approximations to the perimeter include

where the last two are due to Ramanujan (1913-1914), and (71) has a relative error of for small values of . The error surfaces are illustrated above for these functions.

The maximum and minimum distances from the focus are called the apoapsis and periapsis, and are given by

The area of an ellipse may be found by direct integration

The area can also be computed more simply by making the change of coordinates and from the elliptical region to the new region . Then the equation becomes

or , so is a circle of radius . Since

the Jacobian is

The area is therefore

as before. The area of an arbitrary ellipse given by the quadratic equation

is

The area of an ellipse with semiaxes and with respect to a pedal point is

The unit tangent vector of the ellipse so parameterized is

A sequence of normal and tangent vectors are plotted above for the ellipse.

The locus of the apex of a variable cone containing an ellipse fixed in three-space is a hyperbola through the foci of the ellipse. In addition, the locus of the apex of a cone containing that hyperbola is the original ellipse. Furthermore, the eccentricities of the ellipse and hyperbola are reciprocals. The locus of centers of a Pappus chain of circles is an ellipse. Surprisingly, the locus of the end of a garage door mounted on rollers along a vertical track but extending beyond the track is a quadrant of an ellipse (Wells 1991, p. 66). (The envelope of the door's positions is an astroid.)