Abstract
Online social network services have brought a kind of new lifestyle to the world that is parallel to people’s daily offline activities. Social network analysis provides a useful perspective on a range of social computing applications. Social interaction on the Web includes both positive and negative relationships, which is certainly important to social networks. The authors of this article found that the accuracy of the signs of links in the underlying social networks can be predicted. The trust that other users impart on a node is an important attribute of networks. In this article, the authors present a model to compute the prestige of nodes in a trust-based network. The model is based on the idea that trustworthy nodes weigh more. To fulfill this task, the authors first attempt to infer the attitude of one user toward another by predicting signed edges in networks. Then, the authors propose an algorithm to compute the prestige and trustworthiness where the edge weight denotes the trust score. To prove the algorithm’s effectiveness, the authors conducted experiments on the public dataset. Theoretical analysis and experimental results show that this method is efficient and effective.
1 Introduction
Online social network services have brought a kind of new lifestyle to the world that is parallel to people’s daily offline activities. Some popular social network sites, such as Facebook, LinkedIn, and Twitter, have already gathered billions of extensively active users and are still attracting thousands of enthusiastic newbies every day. Doubtlessly, social network has become one of today’s major platforms for people to build friendships and share their interests.
As a great part of the recent research surge on complex networks and their properties, a considerable amount of attention has been devoted to the computational analysis of social networks [2, 15, 16, 18] – structures whose nodes represent people or other entities embedded in a social context, and whose edges represent interaction, collaboration, or influence between entities. Natural examples of social networks include the set of all scientists in a particular discipline, with edges joining pairs who have co-authored articles; the set of all employees in a large company, with edges joining pairs working on a common project; or a collection of business leaders, with edges joining pairs who have served together on a corporate board of directors. The increased availability of large, detailed datasets encoding such networks has stimulated the extensive study of their basic properties, and the identification of recurring structural features.
A network based on trust is quite different from other networks. However, in a trust-based network, two nodes may be close and may be connected but the link may show distrust. More important, a neutral opinion in a trust-based network is very different from a no-connection network. In other words, an edge with 0 weight is different from an edge that is absent. This brings new challenges for trust-based networks as random-walk-based approaches [7] cannot be directly used.
In a trusted network, the prestige of a node depends on the opinions of other nodes, whereas the trustworthiness of a node depends on how a node gives a correct opinion about other nodes. The prestige of a user is based on the opinion of other users, i.e., the opinion of other user which comes in the form of inlinks. The opinion of a user about others is based on their ratings (outlinks). The truthfulness, however, depends on the opinion the other users give in the form of outlinks. The authors refer to truthfulness of a node as bias and prestige of a node as deserve. If a node is biased, its opinion should not weigh significantly. However, if a node deserves (prestige), it mainly relies on nodes that are more truthful.
A node that only gives positive ratings irrespective of what other nodes deserve can be said to have high bias. Similarly, a node that receives positive inlinks from highly biased nodes has a lower deserve value than a node that receive inlinks from truthful nodes.
In this article, the authors present a model to compute the prestige and trustworthiness of nodes in a trust-based network, which is based on the idea that the opinion of trustworthy nodes weighs more. To fulfill this task, the authors first attempt to infer the attitude of one user toward another by predicting signed edges in networks. Then, the authors propose an algorithm to compute the prestige and trustworthiness where the edge weight denotes the trust score. We obtain the trustworthiness of a node by how well it computes the prestige of its neighbors. Unlike most other graph-based algorithms, our method works even when the edge weights are not necessarily positive.
The article is organized as follows: Section 1 is the introduction; Section 2 presents the related works of former scholars; Section 3 describes the algorithm to predict the positive and negative links; Section 4 presents the algorithm to determine the bias and prestige of nodes in networks based on trust scores; Section 5 presents the experimental results; and Section 6 is the conclusion.
2 Literary Review
2.1 Social Network Analysis
Social network analysis (SNA) has a background in sociology [19]. The proliferation of Web 2.0 sites, which focus on users’ participation for content creation, results in very large datasets and call for advanced data mining techniques.
Most of the Web-based SNAs considered the case of unsigned networks, where edges are either unweighted, or only weighted with positive values [19]. Recent studies [6, 22] describe the social network extracted from Essembly, an ideological discussion site that allows users to mark other users as friends, allies, or enemies, discussing the semantics of the three relation types. These works model different types of edges by means of three different graphs. In this article, we try to avoid such overhead and analyze all edges in a single graph with weighted edges.
Works on trusted networks are concerned with negative edges by definition. Works in that field mostly focus on defining global trust measures by using path lengths or adapting PageRank [10]. Collaborative filtering aims at predicting or recommending links in a bipartite user-item graph [11]. The edge weights in such a graph often admit negative values, indicating a dislike of the item in question. However, the methods of collaborative filtering cannot immediately be applied to SNA because links in the bipartite graph are not direct and relations among users extracted from a bipartite graph are necessarily symmetric.
The clustering coefficient was first described by Watts and Strogatz [20] and extended to positively weighted edges by Kalna and Higham [8]. The task of link prediction in social networks is described by Liben and Kleinberg [13] for the case of positive edges. Distance and similarity in unsigned social networks are described by White and Smyth [21]. These measures are based on shortest-path distances and spectral measures such as PageRank and HITS.
Graph theoretic methods for ranking nodes in a network have gained popularity since the introduction of HITS and PageRank algorithms. Subsequently, a number of other methods have also been proposed. Most of these methods are usually a variant of eigenvector centrality measures. For these, however, the edge weights need to be non-negative, as the Perron-Frobenius theorem [4] relies on non-negativity. In a network, where an object can be rated on the basis of explicit ratings such as IMDb and Epinions, or where rating is derived as in the case of peer-to-peer networks, the non-negativity can no longer be enforced. Moreover, by including negative weights, a convergence cannot be guaranteed as the matrix is not stochastic. The algorithm EigenTrust [9] removes negative entries by not considering negative ratings. Ranking has been done on trust-based networks as well when considering negative links, e.g., PageTrust [10]. However, convergence is not guaranteed as the matrix is not stochastic when negative links are included. It has been pointed out by Guha et al. [5] that by removing negative ratings, one cannot distinguish the differences between no-connection and distrust. It was also argued that shifting is not an answer either, owing to many reasons, including the distortion of the semantics of zero score.
2.2 Link Prediction
There is by now a large and rapidly growing literature on the analysis of social networks that have arisen in online domains [17]. As we have noted at the outset, this line of work has almost exclusively treated networks as implicitly having positive signs only. For example, portions of our analysis can be viewed as variants on the problem of link prediction [14] and tie-strength prediction [3]; however, in each case, they can be adapted to take the signs of links into account.
Recently, there are two reports analyzing online social networks that stand out as taking the signs of links into account. Brzozowski et al. [1] studied the positive and negative relationships that exist on ideologically oriented sites such as Essembly; however, their purpose is to predict the outcomes of group votes rather than the broader organization of the social network. Kunegis et al. [12] studied the friend/foe relationships on Slashdot, and computed global network properties, but they did not evaluate theories of balance and status as we are doing here.
3 Predicting Edge Sign
We consider three large online social networks with each link explicitly labeled as positive or negative: Epinions, Slashdot, and Wikipedia. We now consider the problem of predicting the sign of individual edges in our dataset. We give a full network with all but one of the edge signs visible, and are interested in predicting the sign of this single edge whose sign has been suppressed.
3.1 A Machine-Learning Formulation
Given a directed graph G=(V, E) with a sign (positive or negative) on each edge, we let s(x, y) denote the sign of the edge (x, y) from x to y. That is, s(x, y) = 1 when the sign of (x, y) is positive, –1 when the sign is negative, and 0 when there is no directed edge from x to y. Sometimes we are also interested in the sign of a directed edge connecting x and y, regardless of its direction; thus, we write 
when there is a positive edge in one of the two directions (x, y) or (y, x), and either a positive edge or no edge in the other direction. We write 
analogously when there is a negative edge in one of these directions, and either a negative edge or no edge in the other direction. We write 
in all other cases. For different formulations of our task, we suppose that for a particular edge (u, v), the sign s (u, v) or 
are hidden and that we are trying to infer it.
3.1.1 Features
We start by defining a collection of features for our initial machine-learning approach to this problem. The features are divided into two classes: the first class is based on the (signed) degrees of the nodes, which essentially record the aggregate local relations of a node to the rest of the world; the second class is based on the principle from social psychology that we can understand the relationship between individuals u and v through their joint relationships with third parties w. Thus, features of this second class are based on two-step paths involving u and v.
We define the first class of features, based on degree, as follows. As we are interested in predicting the sign of the edge from u to v, we consider outgoing edges from u and incoming edges to v. Specifically we use 
and 
to denote the number of incoming positive and negative edges to v, respectively. Similarly, we use 
and 
to denote the number of outgoing positive and negative edges from u, respectively. We use C (u, v) to denote the total number of common neighbors of u and v in an undirected sense – that is, the number of nodes w such that w is linked by an edge in either direction with both u and v. We will also refer to this quantity C (u, v) as the embeddedness of the edge (u, v).
For the second-class feature, we consider each triad involving the edge (u, v), consisting of a node w such that w has an edge either to or from u and also an edge either to or from v. There are 16 distinct types of triads involving (u, v): the edge between w and u can be in either direction and of either sign, and the edge between w and v can also be in either direction and of either sign; this leads to 24 = 16 possibilities. Each of these 16 triad types may provide different evidences about the sign of the edge from u to v, some favoring a negative sign and some favoring a positive sign. We encode this information in a 16-dimensional vector specifying the number of triads of each type that (u, v) is involved in.
3.1.2 Learning Methodology and Results
We use a logistic regression classifier to combine the evidence from these individual features into an edge sign prediction. Logistic regression learns a model of the form
where x is a vector of features (x1,…,xn) and b0,…,bn are the coefficients we estimate on the basis of the training data.
The edges sign in the networks that we study are overwhelmingly positive. Thus, we consider and evaluate two different approaches. First, we use the full dataset where about 80% of the edges are positive. Second, we follow the methodology of Guha et al. [5] and create a balanced dataset with equal numbers of positive and negative edges, so that random guessing yields a 50% correct prediction rate. For every negative edge (u, v), we sample a random positive edge, which ensures that the number of positive and negative edges in the data we consider for training and prediction is balanced.
3.2 Accuracy of Predicting a Sign of Edge
To test the accuracy of predicting the sign of edge, we consider two different evaluation measures: the classification accuracy and the area under the ROC curve (AUC). For the ease of exposition, we focus on classification accuracy on a balanced dataset. We will discuss later about the robustness of our results on whether we use the full or balanced dataset and whether we evaluate using AUC or accuracy.
We describe each edge (u, v) in this set using the two classes of features described above. We consider all 23 features together (denoted by All23), and we also evaluate performance using the features of each class separately – that is, representing each edge as a 7-dimensional vector of degree features and as a 16-dimensional vector of triad features. We also consider performance across different types of edges. In particular, as the triad features are relevant only when u and v have neighbors in common, it is natural to expect that they will be most effective for edges of greater embeddedness. We therefore consider the performance restricted to subsets of edges of different levels of minimum embeddedness.
The classification accuracy is shown in Figure 1, where results are described for all three datasets, for the two classes of features separately and together, and for different levels of minimum embeddedness (denoted by Em). Several observations stand out. First, prediction based on the learned models significantly outperforms the results reported by Guha et al. [5] for the Epinions dataset. The lowest error rate achieved in their article is 14.7%, whereas we obtained error rates of 11.45% for Degree, 6.64% for 16Triads, and 6.58% for All23.
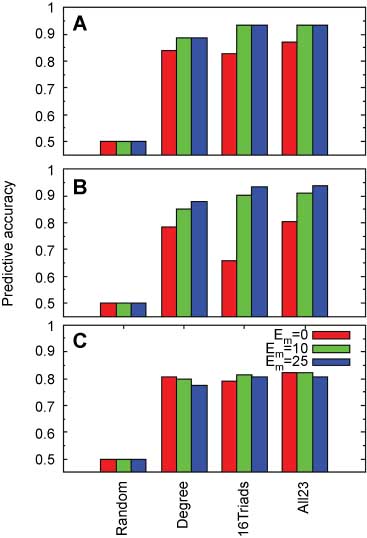
Accuracy of Predicting a Sign of Edge in Network. (A) Epinions, (B) Slashdot, (C) Wikipedia.
These results are particularly interesting because our features are based only on local properties in the one-step neighborhood of the edge (u, v) whose sign is being inferred, in contrast with the propagation model of Guha et al. [5]. This suggests that edge signs can be meaningfully understood in terms of such local properties, rather than requiring a notion of propagation from farther-off parts of the network.
In all experiments, we report the average accuracy and estimated logistic regression coefficients over 10-fold cross validation. If not stated otherwise, we will limit our analyses to edges with a minimum embeddedness of 25. We note that our results are robust with respect to training dataset and evaluation metric. Generally, when using the full dataset rather than the balanced one, random guessing improves accuracy from 50% to approximately 80%. With the full dataset, the accuracy of our logistic regression method correspondingly jumps to the 90–95% range and maintains roughly a 15% absolute improvement over random guessing. When evaluating using AUC rather than accuracy, the overall pattern of performance does not change. The various forms of logistic regression have an AUC of approximately 90% on the balanced dataset and 95% on the full dataset.
4 The Algorithm to Compute Bias and Prestige of Nodes
The goal of the analysis not only lies in predicting the edge signs themselves but also in presenting a model that computes the prestige and trustworthiness of nodes in a network based on the observed patterns of positive and negative edges. It is based on the idea that the opinion of trustworthy nodes weighs more. We obtain the trustworthiness of a node by how well it computes the prestige of its neighbors.
We model the trust-based networks by using graphs where the edge weight indicates the user opinion. If a user does not rate, then there is no edge. If a user gives a neutral rating, it is denoted by the edge weight of 0. As we discussed earlier, this is significantly different from a no-connection, as the absence of an edge indicates that the user did not rate. Likewise for the latter case, where the user has to give only positive scores, the edge weights attain only non-negative values. Here, an explicit 0 score implies very low confidence, but is again quite different from a no-connection that signifies no rating.
Formally, let G = {V, E} be a graph, where an edge euv ∈ E (directed from node u to node v) has weight wtuv ∈ [–1, 1]. We say that node u gives the trust score of wtuv to node v.
Let dout(u) denote the set of all outgoing links from node u and, likewise, din(u) denote the set of all incoming links to node u. In this work, we measure two attributes of a node:
Trustworthiness: This reflects the expected weight of an outgoing edge.
Prestige: This reflects the expected weight of an inlink from an unbiased node.
4.1 Definitions
The trustworthiness of a node is using its propensity to trust/mistrust other nodes. Thus, the propensity or trustworthiness of a node can be measured by the differences between the rating a node provides to another node (i.e., the edge weight) and the “ground” truth, i.e., what the second node truly deserves (this takes into account the trust by other nodes). The trustworthiness of a node u is given by
Normalization is done to maintain the value of trustworthiness in the range of [–1, 1]. A node is truly truthful if it has a trustworthiness of 0.
A node has a positive bias if it has a propensity to give positive outlinks and a negative trustworthiness otherwise. A node giving a positive rating to other nodes that do not deserve such ratings would attract a high trustworthiness. Using trustworthiness, the inclination of a node toward trusting/mistrusting is measured. It can also be used to understand the true nature of a node. If a high-trustworthiness node (either positive or negative) gives a rating, then such score should be given less importance. We can do so by reducing the effect of trustworthiness from each outlink a node gives. For example, if a node with a high positive bias gives an outlink with large positive weight, then the weight is reduced from this edge while calculating the rating of the other node. Similarly, negative weights from a negative trustworthiness node are reduced. However, if a node has an edge whose weight has an opposite sign to that of the bias, we do not make any changes. Intuitively, when a person is known to give a negative feedback in general, actually he/she gives a positive feedback, thus his/her opinion should weigh significantly. Therefore, if a node has a positive (negative) trustworthiness and has an edge with negative (positive) weight, then we do not make any change to the edge weight.
We introduce an auxiliary variable Xkv to measure the effect of trustworthiness of node k on its outgoing edge to node j per unit edge weight:
From the above expression, we can see that when trustworthiness and edge weight are of opposite signs, Xkv becomes zero and there is no effect of the trustworthiness. Otherwise, Xkv becomes the absolute value of the trustworthiness.
We can now reduce the edge weight using the effect of trustworthiness, i.e., Xkv. The new weight 
is scaled from the old weight as follows:
If edge weight and bias are of opposite signs, the new weight remains the same; otherwise, it is reduced.
The prestige value of a node represents the true trust a node deserves. We can use trustworthiness to define prestige. Prestige is the expected weight of an incoming link from an untrustworthiness node. The prestige value depends on the quality of the inlinks but not on the quantity: prestige of a node with one quality inlink is equivalent to a node with many quality inlinks. This definition differs from the usual random-walk-based methods where the numbers of inlinks matter. For each inlink, we remove the effect of bias from the weight and then we compute the mean of all inlinks. The prestige of a node v is given by
4.2 Computing Trustworthiness and Prestige
In this section, we describe an algorithm to find the trustworthiness and prestige values of all nodes in the network. Note that the definitions as given in Eqs. (2) and (5) are mutually recursive. Trustworthiness of a node depends on the prestige of its neighbors, which, in turn, depends on the trustworthiness of their neighbors and so on. Thus, to solve this, we use the method of fixed-point iteration.
We denote the trustworthiness and prestige of node v at iteration t by trustworthinesst(u) and prestiget(u), respectively. We use values obtained from iteration t to compute the values for iteration t+ 1. From the initial values of trustworthiness and prestige, prestige values at the next iteration are computed for all nodes. Then, using those values, the trustworthiness values are reestimated. Thus, prestiget+ 1(u) depends on trustworthinesst(*), which, in turn, is computed using prestiget(*). Equations (2) and (5) can be now rewritten as
5 Result of the Experiments
In this section, we will describe the different experiments that are done on real trust-based networks with the measures of trustworthiness and prestige in detail.
5.1 Dataset
We consider two large online social networks where links are explicitly positive or negative, Epinions and Slashdot, for performing the experiments: (i) the trust network of the Epinions product review Web site, where users can indicate their trust or distrust of the reviews of others; (ii) the social network of the blog Slashdot, where a signed link indicates that one user likes or dislikes the comments of another.
Table 1 gives statistics for all three datasets. Our networks have approximately tens to hundreds of thousand nodes in order, but less than a million edges. In each network, the edges are inherently directed, as we know which user created the edge. In all networks, the background proportion of positive edges is about the same, with roughly 80% of the edges having a positive sign.
Dataset Statistics.
| Epinions | Slashdot | |
|---|---|---|
| Nodes | 119.22 | 82,144 |
| Edges | 841,200 | 549,202 |
| +Edges | 85% | 77% |
| –Edges | 15% | 23% |
| Triads | 13,375,407 | 1,508,105 |
5.2 Distribution of Trustworthiness and Prestige
The first set of experiments measure the distribution of trustworthiness and prestige values of the nodes. The distribution of prestige values are compared against that of the indegree mean. The indegree mean for a node is defined as the average weight of incoming links. Figure 2 shows the histograms of the indegree mean and deserve value for Slashdot datasets. In the dataset, the numbers of nodes with indegree mean 1 is very high; the count of nodes with indegree mean –1 is also significant in number. The count of nodes with indegree mean as 1 is very high. This is primarily because >80% of the edges have positive weight.
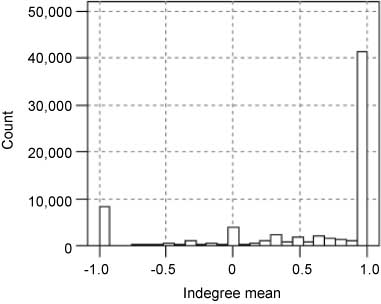
Distribution of Indegree Mean for Slashdot.
Figure 3 shows the result of the distribution of prestige; as shown in the figure, the distribution of prestige is smoother owing to the removal of the effect of trustworthiness. Figure 4 shows the distribution of trustworthiness values for both datasets. It can be observed that the distribution is mostly concentrated around 0 and is positively skewed. This indicates that a significant fraction of the edges have positive weights. The trustworthiness values have little correlation with the mean of the outgoing edge weights.
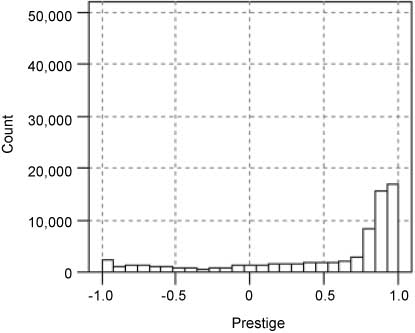
Distribution of Prestige for Slashdot.
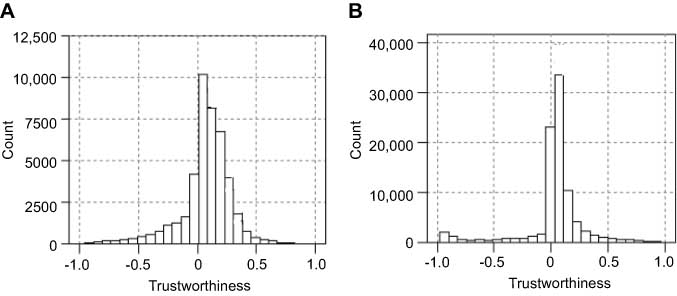
Distribution of Trustworthiness Values. (A) Dataset for Slashdot, (B) Dataset for Epinions.
5.3 Comparison of Trustworthiness with Prestige
In the second experiment, we want to test the effect of bias versus deserve. Typically, we expect a node with high prestige to be more trustworthy, i.e., have low trustworthiness. In case a node receives many positive inlinks but has outlinks that do not conform well to the opinion of other nodes, then we say that node has a high prestige score but has high trustworthiness.
In Figure 5, we plotted the histogram of prestige versus trustworthiness. We divided the trustworthiness into many bins of equal sizes, and then we computed the mean of prestige lying in that bin. Here, we consider only those nodes that have both prestige and trustworthiness values.
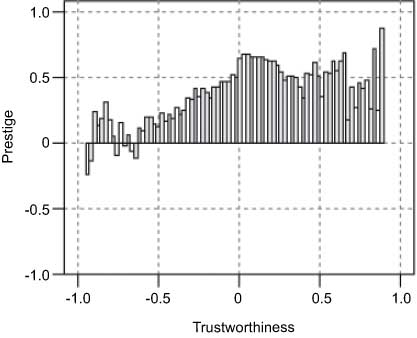
Comparison of Trustworthiness and Prestige for Slashdot Dataset.
In Figure 5, we can observe that nodes with high trustworthiness (usually gives more positive links) also have high prestige value, showing the strong relationship between the trustworthiness and prestige. It shows that a node giving positive ratings is respected as well.
6 Conclusion
For many applications involving trust-based networks, it is crucial to assess the prestige or trustworthiness. In this article, we have proposed an algorithm to compute the bias and prestige of nodes in networks where the edge weight denotes the trust score. Moreover, our methods for sign prediction yield performance could significantly improve the finding of the prestige of nodes in networks based on trust scores. Unlike most of the other graph-based algorithms, our method works on even the edge weights that are not necessarily positive. The experiments showed that our model is effective.
There are a number of further directions suggested by this work. A first one is, of course, to explore methods that might yield a still better performance for the basic sign prediction problem, and to understand whether the features that are relevant to more accurate methods help in the further development of social theories of signed links.
The research is supported by the Natural Science Foundation of Jiangsu Province, No. BK2008190, and open technology fund project of Jiangsu Province R&D Institute of Marine Resources, No. JSIMR11B12.
Bibliography
[1] M. J. Brzozowski, T. Hogg and G. Szabó. Friends and foes: ideological social networking, in: Proc. ACM CHI, 2008.10.1145/1357054.1357183Search in Google Scholar
[2] B. Ceren, A. Divyakant and E. A. Amr, Limiting the spread of misinformation in social networks, in: Proceedings of the WWW2011, pp. 665–674, 2011.Search in Google Scholar
[3] E. Gilbert and K. Karahalios, Predicting tie strength with social media, in: Proc. ACM CHI, 2009.10.1145/1518701.1518736Search in Google Scholar
[4] G. Golub and C. F. V. Loan, Matrix computations, Johns Hopkins University Press, Baltimore, MD, 1996.Search in Google Scholar
[5] R. V. Guha, R. Kumar, P. Raghavan and A. Tomkins, Propagation of trust and distrust, in: Proceedings of WWW2004, pp. 403–412, 2004.10.1145/988672.988727Search in Google Scholar
[6] T. Hogg, D. Wilkinson, G. Szabo and M. Brzozowski, Multiple relationship types in online communities and social networks, in: Proceedings of AAAI, pp. 556–565, 2008.Search in Google Scholar
[7] B. D. Hughes, Random walks and random environments, Oxford University Press, New York, 1996.Search in Google Scholar
[8] G. Kalna and D. J. Higham, A clustering coefficient for weighted networks, with application to gene expression data, AI Commun. 20 (2007), 263–271.Search in Google Scholar
[9] S. D. Kamvar, M. T. Schlosser and H. G. Molina, The eigentrust algorithm for reputation management in P2P networks, in: Proceedings of WWW2003, pp. 640–651, 2003.10.1145/775152.775242Search in Google Scholar
[10] C. Kerchove and P. V. Dooren, The PageTrust algorithm: how to rank web pages when negative links are allowed? in: Proceedings of the SIAM, pp. 346–352, 2008.10.1137/1.9781611972788.31Search in Google Scholar
[11] Y. Koren, Factor in the neighbors: scalable and accurate collaborative filtering, ACM Trans. Knowl. Discov. Data 4 (2009), 1–24.10.1145/1644873.1644874Search in Google Scholar
[12] J. Kunegis, A. Lommatzsch and C. Bauckhage, The Slashdot Zoo: mining a social network with negative edges, in: Proc. WWW, 2009.10.1145/1526709.1526809Search in Google Scholar
[13] N. D. Liben and J. Kleinberg, The link prediction problem for social networks, in: Proceedings of International Conference on Information and Knowledge Management, pp. 556–559, 2003.Search in Google Scholar
[14] D. Liben-Nowell and J. Kleinberg, The link-prediction problem for social networks, J. Am. Soc. Inf. Sci. Technol. 58 (2007), 1019–1031.10.1002/asi.20591Search in Google Scholar
[15] W. Q. Lin, X. N. Kong and S. Y. Philip, Community detection in incomplete information networks, in: Proceedings of the WWW2012, pp. 341–350, 2012.10.1145/2187836.2187883Search in Google Scholar
[16] K. Liran, L. Edo and S. Oren, Estimating sizes of social networks via biased sampling, in: Proceedings of the WWW2011, pp. 597–604, 2011.Search in Google Scholar
[17] M. E. J. Newman, The structure and function of complex networks, SIAM Rev. 45 (2003), 167–256.10.1137/S003614450342480Search in Google Scholar
[18] B. Pang and L. Lee, Opinion mining and sentiment analysis, Found. Trends Inf. Retriev. 2 (2008), 144–155.Search in Google Scholar
[19] J. Scott, Social network analysis, Sage Publications, London, 2000.Search in Google Scholar
[20] D. J. Watts and S. H. Strogatz, Collective dynamics of ‘small-world’ networks. Nature 393 (1998), 440–442.Search in Google Scholar
[21] S. White and P. Smyth, Algorithms for estimating relative importance in networks, in: Proceedings of International conference on Knowledge Discovery and Data Mining, vol. 19, pp. 266–275, 2003.10.1145/956750.956782Search in Google Scholar
[22] B. Yang, W. Cheung and J. Liu, Community mining form signed social networks, Knowl. Data Eng. 19 (2007), 1333–1348.10.1109/TKDE.2007.1061Search in Google Scholar
©2013 by Walter de Gruyter Berlin Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
