Open Access Published by De Gruyter June 14, 2022

Personalized recommendation system based on social tags in the era of Internet of Things

Jie Dong , Gui Li , Wenkai Ma and Jianshun Liu

From the journal Journal of Intelligent Systems

https://doi.org/10.1515/jisys-2022-0053

Abstract

With the rapid development of the Internet, recommendation systems have received widespread attention as an effective way to solve information overload. Social tagging technology can both reflect users’ interests and describe the characteristics of the items themselves, making group recommendation thus becoming a recommendation technology in urgent demand nowadays. In traditional tag-based recommendation systems, the general processing method is to calculate the similarity and then rank the recommended items according to the similarity. Without considering the influence of continuous user behavior, in this article, we propose a personalized recommendation algorithm based on social tags by combining the ideas of Markov chain and collaborative filtering. This algorithm splits the three-dimensional relationship of <user-tag-item> into two two-dimensional relationships of <user-tag> and <tag-item>. The user’s interest degree to the tags is calculated by the Markov chain model, and then the items corresponding to them are matched by the recommended tag set. The influence between tags is used to model the satisfaction of items based on the correlation between the tags contained in the matched items, and collaborative filtering is used to complete the sparse values when calculating the interest and satisfaction between user–tags and user–items to improve the accuracy of recommendations. The experiments show that in the publicly available dataset, the personalized recommendation algorithm proposed in this article has significantly improved in accuracy and recall rate compared with the existing algorithms.

Keywords: social tag; Markov chain; satisfaction model; collaborative filtering; personalized recommendation

1 Introduction

With the continuous development of Internet of Things (IoT) technology, more and more smart devices and smart services are entering people’s life, which continuously help people to get more convenient life experience. At the same time, a large amount of redundant information causes information overload, so IoT service recommendation becomes an important research content of IoT and presents an increasingly important role. The emergence of social tags has brought new opportunities to recommendation technology and gradually become a research hotspot.

Recommendation algorithms are divided into two categories in terms of the connection goals achieved: rating prediction and behavior prediction. The personalized recommendation based on the user’s historical behavior records used in this article belongs to behavior prediction. Usually, these behaviors can be represented by a user–item bipartite graph, and there is a binary relationship between them, and by far, the most successful technique to deal with this relationship is the collaborative filtering algorithm, which finds similar users or items by the similarity or overlap between users and users or items and items to achieve the purpose of recommending items preferred by users. In addition to the aforementioned two user-based or item-based approaches, the relationship between users and items can also be connected by auxiliary information, by some features to link users and items, which can be represented by using a three-part user–tag–item graph, and there is a ternary relationship between the three [1]. The user is recommended those items that have the features that the user likes. Of course, there are different ways to express the features here, for example, they can be expressed as a latent semantic vector or as a set of attributes of the items (e.g., for real estate, the set of attributes includes the location of the property, the attribution of the school district, the attributes of the railroad house, the price level).

Traditional recommendation systems based on Markov chain (MC) models can predict a user’s next behavior based on the user’s most recent behavior using continuous behavioral data with time-series attributes [2,3]. The continuous behavior of users is simulated by learning the transfer matrix of their preferred items. Ref. [4] proposed a collaborative filtering recommendation algorithm based on labeled topics, using Dirichlet distribution modeling to mine potential semantic topics and eliminate the semantic ambiguity problem existing in labels to improve the recommendation effect. Ref. [5] proposed a hybrid collaborative filtering recommendation algorithm based on “user–item–user interest label graph” to improve the accuracy of Top-N recommendation by improving the material diffusion recommendation algorithm based on “user–item–label” three-part graph. However, all of these algorithms’ do not pay attention to the impact caused by the continuous behavior of users on the recommendation effect. In this article, we use the Markov chain model to simulate the information contained in users’ continuous behaviors, by learning the transfer matrix of users’ preferences, so as to predict the set of labels preferred by users’ next behavior based on the set of labels contained in the most recent behavior.

The set of labels preferred by the next user behavior can be obtained by Markov chains. The next difficulty is how to measure the attractiveness of an item containing the user’s preferred set of tags to the user. A simple and intuitive approach is to calculate the user’s attractiveness score for each tag in an item by using the tag frequency derived from historical information and then aggregating them into the user’s score for that item. However, this approach only considers each tag individually but ignores the effects between tags. Instead, user satisfaction with one tag is also affected by user satisfaction with other tags. In other words, to a certain extent, the tags can reinforce each other to attract users. For example, when choosing to buy a house, users usually have their own different needs, but these needs are also related to each other, such as key basic schools, large shopping malls and supermarkets, convenient transportation, and suitable price. If only independent tags are considered and the influence between tags is ignored, it will affect the recommendation effect. Therefore, it is necessary to consider the influence between labels when making Top-N recommendations. In this article, we propose a model to estimate the interaction between tags as a basis for Top-N recommendation.

2 Related work

With the development of Web 2.0, most of the tagging data taken nowadays are social tags based on mass taxonomy. Recent recommendation algorithms based on social tags are usually divided into three categories: (i) tensor based, (ii) graph theory based, and (iii) topic based. In this article, we adopt the Markov chain model to deal with continuous behavior data to improve the recommendation effect. Recent studies on Markov chains have been limited to the two-dimensional relationship data between users and items, such as Steffen Rendle who used Markov chains to build transfer matrices to predict users’ next purchases. Reference [6] proposed a recommendation algorithm based on the Markov decision process using the heuristic algorithm to improve the maximum likelihood estimation of Markov chain state transfer.

In this article, we first split the three-dimensional user–label–item relationship into two two-dimensional relationships, user–label and label–item; introduce the Markov chain model in calculating the user-to-label preferences; and use the transfer matrix to calculate the set of preferred labels contained in the user’s next behavior, which has the following advantages: (i) Effectively improves the personalized recommendation effect of the user, the label-based recommendation uses the current user-provided historical behavior to construct personalized transfer matrix of user preferences, while collaborative filtering only requires static user rating data to discover users’ immediate neighbors. (ii) Further enhances the recommendation interpretation by displaying a list of item content features or descriptions in the recommendation list to improve users’ trust in the recommendation results. Later, satisfaction models are constructed, and user satisfaction with items is calculated when targeting the association between tags and items.

Tag-based recommendation algorithms are the classical PageRank [7] and the FolkRank [8] algorithms inspired by it. The PageRank algorithm recommends high relevance among labels by “rewarding,” while the FolkRank algorithm uses a three-part graph (user set, item set, and label set) to transfer weights to each other to improve its own weight to achieve this goal. In the study of tag-based item ranking, this article is inspired by Pham TAN et al. [9] on the modeling of points of interest among geographic regions and the association between points of interest to construct user satisfaction with items through tags and to explore the influence of different tags on user satisfaction with items. In this way, we propose a model of user satisfaction based on the association between tags, using the similarity of tags and the similarity of items to complete the relevant sparse data [10,11], construct a model of user satisfaction with item by the historical information of tags and the interaction between tags and optimize it, and finally personalize Top-N recommendations to users with this satisfaction.

3 User-to-label prediction algorithm based on Markov chains

3.1 Label-based personalized Markov chain transfer matrix estimation

For each user u, the information contained in its historical behavior, which equal to the set of tags, is ℬ u = ( B 1 u , … , B t u ) , and B t u ⊆ T denotes the set of tags of the items that user u queries or browses at moment t. The historical labels of all users are ℬ ≔ { ℬ u 1 , … , ℬ u m } .

Usually, a Markov chain with step number k is defined as follows:

(3.1) p ( X t = x t | X t − 1 = x t − 1 , X t − 2 = x t − 2 , … , X t − k = x t − k ) ,

where X t , … , X t − k are random variables and x t − k are their specific instances. To simplify the transfer probability matrix, the number of steps of the Markov chain k is set as 1, The simplified Markov chain is expressed as follows:

(3.2) p ( B t u | B t − 1 u ) .

Similarly, the Markov chain for each user is expressed through the transfer matrix between labels, but here the Markov chain is individualized as follows:

(3.3) a u , t l , t i ≔ p ( t i ∈ B t u | t l ∈ B t − 1 u ) .

Based on the label information given by the user’s last state, the likelihood of user preference for a label is mined, which can be interpreted as the average value in the transfer matrix from the user’s last query to the query for this label.

(3.4) p ( t i ∈ B t u | B t − 1 u ) ≔ 1 ∣ B t − 1 u ∣ ∑ t l ∈ B t − 1 u p ( t i ∈ B t u | t l ∈ B t − 1 u ) .

This means that for each user u, a personalization transfer matrix A u ∈ ℝ m × m is created [12]. Let label t _l transfer to label t _i be a state pair (t _l, t _i), and t l ∈ B t − 1 u , t i ∈ B t u , C t l , t i u denotes the number of occurrences of state pair (t _l, t _i) in user u’s historical label set B ^u. For each user u, the transfer probability formula for label t _l to label t _i is noted as follows:

(3.5) A t l , t i u = C t l , t i u / ∑ t i l C t l , t i u , ∑ t i l C t l , t i u ≠ 0 , 0 , ∑ t i l C t l , t i u = 0 .

3.2 User’s interest degree model for tags

Constructing user’s interest degree on tags

In the study of two dimensional relationship, based on the Markov chain model according to the known set of labels contained in the user’s most recent behavior and the user’s personalized label transfer matrix A ^u, refer to equation (3.4) to construct the probability matrix I(u,t) of the user’s preference for the label in the next behavior, the user’s interest degree matrix for the tag.

Due to the sparsity of user’s historical behavior data, the matrix I(u,t) also has data sparsity. Therefore, while introducing the idea of collaborative filtering, the similarity of tags is combined to complement the matrix of users’ interest in tags, and if there are no data sparsity, then this step is not necessary.

If it is believed that different labels on the same item have a certain degree of similarity, then when two labels appear in the label set of many items at the same time, it can be considered that the two labels have a greater degree of similarity. The number of labeling tags is also considered, and hence, the Cosine coefficient is used for calculation, which is calculated as follows:

(3.6) cossimt , t ′ = ∑ i ∈ N ( t ) ∩ N ( t ′ ) n t , i n t ′ , i ∑ i ∈ N ( t ) n t , i 2 ∑ i ∈ N ( t ′ ) n t ′ , i 2 ,

where n t , i , n t ′ , i denotes the number of times item i is labeled t as well as label t′, and N ( t ) , N ( t ′ ) denotes the set of items labeled with label t as well as label t′.

In summary, the degree of user interest in the labels after completing the sparse values is calculated as follows:

(3.7) I ′ ( u , t j ) = ∑ i = 1 l I ( u , t i ) ∗ cossim ( t i , t j ) .

Through Markov chain and collaborative filtering ideas based on labels to discover the set of labels preferred by users, the size of the label set T should need to be adjusted accordingly to the actual situation.

4 Probabilistic model-based tag-to-item ranking algorithm

Through the improving Markov chain, the T tags that the next item queried by the user is known to have. By the set of discovered tags, the corresponding n items are matched and then Top-N recommendation is performed, where n ≥ N . In the process of tag matching items, there will be a situation where the number of tags of the items is more than the recommended T tags.

4.1 Top-N recommendation

The user satisfaction model for items based on tags is constructed based on the number of times users label the items. However, in the tag-based item recommendation problem, the item does not contain a single tag, but a set of tags. Existing ranking algorithms usually assume that the relationships between the tags contained in the set of item tags are independent of each other. However, the relationships among the labels are mutually influential.

Consider an item I r ≔ { t i 1 , ⋯ , t i k } containing multiple labels, and S _i1…ik denotes the satisfaction of user u with item I r labeled with labels t i 1 , ⋯ , t i k . Let p u ( t i 1 , ⋯ , t i k | k ) be the probability of user u querying label t i 1 , ⋯ , t i k , and the user will query k different labels, k ∈ [ 1 , l ] . When user u queries according to the set of tags, user u’s total expected satisfaction can be expressed as S _total, defined as follows:

(4.1) S total = ∑ t i 1 ∈ T S i 1 p ( t i 1 | k = 1 ) p ( k = 1 ) + ∑ t i 1 , t i 2 ∈ I r S i 1 i 2 p ( t i 1 , t i 2 | k = 2 ) p ( k = 2 ) + ⋯ + ∑ t i 1 , ⋯ , t i ∣ I r ∣ ∈ I r S i 1 ⋯ i ∣ I r ∣ p ( t i 1 , ⋯ , t i ∣ I r ∣ | k = ∣ I r ∣ ) p ( k = ∣ I r ∣ ) .

Since the number of tags used when users actively use tags to query items is mostly only 1 or 2. Therefore, in this article, we only consider the first and second terms in S _total and ignore other higher-order terms. At this point, S _total is represented as follows:

(4.2) S total ≈ ∑ t i 1 ∈ I r S i 1 p ( t i 1 | k = 1 ) p ( k = 1 ) + ∑ t i 1 , t i 2 ∈ I r S i 1 i 2 p ( t i 1 , t i 2 | k = 2 ) p ( k = 2 ) .

In this article, two probabilities will be defined: p ( t i 1 | k = 1 ) and p ( t i 1 , t i 2 | k = 2 ) . The probability p ( t i 1 | k = 1 ) represents the probability that user u queries t _i1, which equals to p ( t i 1 | k = 1 ) = p ( t i 1 | u ) , which can be calculated by using a recommendation model such as memory-based collaborative filtering [13] or matrix decomposition. For the probability p ( t i 1 , t i 2 | k = 2 ) , assuming that users query different tags independently of each other, a simple approach is to define this probability as p ( t i 1 , t i 2 | k = 2 ) = p ( t i 1 | u ) ⋅ p ( t i 2 | u ) . However, as mentioned earlier, the user’s interest in tags may be influenced by other tags, which means that the influence between tags cannot be ignored. Therefore, in the model of this article, its joint probability is defined by equal probability as p ( t i 1 , t i 2 | k = 2 ) = 1 2 ( p ( t i 2 | t i 1 ) ⋅ p ( t i 1 | u ) + p ( t i 1 | t i 2 ) ⋅ p ( t i 2 | u ) ) , where p ( t i 1 | t i 2 ) is the transfer probability from t _i2 to t _i1, which can be obtained from historical behavioral data and is calculated as follows:

(4.3) p ( t i 1 | t i 2 ) = # Users who queried both t i 1 and t i 2 # Users who queried t i 2 .

The probabilities p ( t i 1 | k = 1 ) and p ( t i 1 , t i 2 | k = 2 ) are defined only based on the historical behavior data of the users. However, a more complex definition of these probabilities can be given by integrating additional information. For example, the probability of querying two tags can be increased (or decreased) if they are known to be complementary (or substitutable) to each other. In addition, other methods (e.g., classification or textual information) can be used to compute query probabilities. The definition of satisfaction S _i1i2,…,ik is given. Usually, the more labels a user queries, the higher satisfaction the user obtains. Therefore, in this article, we set S _i1 = 1, S _i1i2 = 2, …, S _i1i2,…,ik= k in the project, and other satisfaction functions can be defined according to different application requirements. Thus, the expected satisfaction S _total can be re-expressed as follows:

(4.4) S t o t a l ≈ β ⋅ ∑ t i ∈ I r p ( t i | u ) + ∑ < t i , t j > ∈ O I r p ( t i | t j ) ⋅ p ( t j | u ) p ( k = 2 ) ,

where O I r represents all ordered pairs < t i , t j > in I r , and β = P ( k = 1 ) P ( k = 2 ) is the user-related parameter. However, it is very difficult to set β for each user; therefore, in this article, β is set to 1 because it provides the best effect for the satisfaction model and thus improves the accuracy of the recommendation.

4.2 Complementary Top-N recommendations

As mentioned earlier, items with T tags can be matched. At this point, if the data have sparsity, sometimes it may not be matched or only a few items with T tags can be matched, so when T < N , this section needs to complete the N − T satisfaction of the recommendation to the user by the user’s interest in the item in a collaborative filtering way.

This section uses labels to calculate the similarity between items, mainly based on the principle that the more times item i and item i′ are labeled with the same label by users, the more similar item i and item i′ are. Also, considering that only concern about whether the label is labeled, n t , i and n t , i ' denote whether item i and item i′ are labeled with label t, being labeled takes the value of 1, otherwise 0. N ( i ) , N ( i ′ ) denote the set of labels of item i and item i′, respectively, and use the Jaccard coefficient for the calculation, and the calculation formula is expressed as follows:

(4.5) Jaccardsim ( i , i ′ ) = ∑ t ∈ N ( i ) ∩ N ( i ′ ) n t , i n t , i ′ ∑ t ∈ N ( i ) n t , i 2 + ∑ t ∈ N ( i ′ ) n t , i ′ 2 − ∑ t ∈ N ( i ) ∩ N ( i ′ ) n t , i n t , i ′ .

Completing the user’s satisfaction with the item, obtaining the user u’s satisfaction with the recommended item i according to S a t ( u , i ) , calculating the similarity between the recommended item i and the new item i′ to be recommended, and finding the user u’s satisfaction with the new item i′ to be recommended, we obtain:

(4.6) S a t ′ ( u , i ′ ) = ∑ i = 1 n S a t ( u , i ) ⁎ Jaccardsim ( i , i ′ ) .

Finally, use user’s satisfaction with the item S a t ′ ( u , r ) to complement user’s Top-N recommendation for the item. After building a Markov chain model of users’ interest in tags and constructing a model of users’ interest in items by T tags, we use the correlations between tags to construct a model of users’ satisfaction ranking of items.

5 Algorithm design

The personalized tag recommendation algorithm based on Markov chain and collaborative filtering proposed in this article mainly considers tags as an important link resource between users and items. After establishing the Markov chain model of user’s interest in tags and the T-tag model of user’s interest in items, we use the correlation between tags to construct the ranking model of user’s satisfaction with items. A top-N recommendation list is generated by evaluating the similarity between item-based tags and the similarity between tag-based items. The specific algorithm is described as follows.

Input: training set, test set, T-value, and K-value

Output: Top-N recommendation for target users

Step 1: Decompose the user–tag–item 3D relationship into two 2D relationships: user–tag and tag–item. The user’s personalized tag transfer matrix is calculated in the user–tag relationship according to equation (3.5), and then the interest degree of the user’s next behavior on the tag is calculated according to equation (3.4).

Step 2: Calculate the similarity of tags to complement the user interest model I′(u,t) for the tags. The similarity between tags was assessed based on the number of times two different tags were tagged simultaneously on many different items. The similarity of tags is calculated by using the Cosine coefficient according to equation (3.6), and the user’s interest in tags after completing the sparse value is obtained according to equation (3.7).

Step 3: Construct the user satisfaction model for the items. Match items based on the user preference label set ∣ T ∣ and construct the user satisfaction model S a t ( u , i ) for the matched items according to equation (4.2).

Step 4: Calculate the similarity of items. The similarity between items is evaluated based on the number of times different items are labeled by the same label, and the Jaccard coefficient is used to calculate the similarity of items according to equation (4.5).

Step 5: Predict the target users’ satisfaction with the new items to be recommended. Based on the constructed user satisfaction model for the items and the similarity Jaccadsim ( x , y ) between the new items to be recommended and the known labeled items, the user satisfaction for the new items is calculated according to equation (4.6).

Step 6: Sort the predicted satisfaction of target users for new items in a descending order and take out the top N items as Top-N recommendation list and output it.

6 Experimental analysis

The experimental environment was implemented on a Window 10 platform 64-bit system with Intel-i7, 2.60 GHz processor, 8GB RAM, and 1TB hard disk, using Python 3.6 language programming. Real datasets Movielens (http://movielens.org) were used for experimental validation. The number of user, item, and tagging behavior records in the dataset is shown in Table 1.

Table 1

Experimental data set Movielens

Dataset	Number of users	Items	Tag behavior records
Ml-latest	18,052	25,308	753,171

Movielens is the oldest recommendation system that allows users to tag movies with tags. The ml-latest dataset provided by this dataset is used, which has 18,052 users, 25,308 movies tagged, and 753,171 user-labeled tag records.

Table 2

Experimental data set Movielens-20 m and its core subset

Dataset	Number of users	Items	Tag behavior records	Dataset
Ml-20m	7,801	19,545	38,643	4,65,564
Core Subsets	50	634	1,340	46,846

In Top-N recommendation, precision and recall are used in the classical evaluation metrics. But in the experiments, since there is a trade-off between accuracy and recall, this article also uses F-measure to evaluate accuracy and recall. Accuracy represents the probability that the user is interested in the final generated recommendation list, and recall represents the probability that the user’s true favorite items are included in the final generated recommendation list. The data set in Table 1 is randomly divided into two parts, 90 and 10%, with the former as the training set and the latter as the test set. Let R(u) denote the Top-N recommendation list made to users based on their behavior on the training set, and T(u) denote the set of items actually selected by users after the system recommends labels to them. The evaluation metrics accuracy and recall and F-measure are defined as follows:

(5.1) Precision = ∑ u ∈ U ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∈ U ∣ R ( u ) ∣ ,

(5.2) Recall = ∑ u ∈ U ∣ R ( u ) ∩ T ( u ) ∣ ∑ u ∈ U ∣ T ( u ) ∣ ,

(5.3) F -measure = 2 ⁎ Precision ⁎ Recall Precision + Recall ,

(5.4) DCG k u = r u c 1 + ∑ i = 2 k r u c i log 2 ( i ) ,

(5.5) nDCG k u = DCG k u IDCG k u .

The social labeling-based personalized recommendation algorithm MCTS is compared experimentally with three classical algorithms: the standard tensor decomposition-based algorithm (FPMC) and the FolkRank algorithm [8] (defined as FR) and the labeling-based collaborative filtering algorithm (defined as TCF) to obtain the accuracy, recall, and F-measure of each algorithm.

Figure 1 shows that as the number of recommended items increases, the accuracy decreases and the recall increases significantly for the MCTS, FPMC, FR, and TCF algorithm recommendations. When the F value is the highest, it indicates that the best-combined effect of recommendation is achieved at this time. The MCTS algorithm, which incorporates the MC model, satisfaction model, and collaborative filtering ideas, is found to have improved accuracy, recall, and F-value compared with the existing recommendation algorithms FPMC, FR, and TCF, indicating that the algorithm proposed in this article can not only effectively use the user’s historical continuous behavior records but also improve the data sparsity, further arguing that tags can express the user’s interests and characteristics of items, which can effectively improve the accuracy of recommendations.

Figure 1

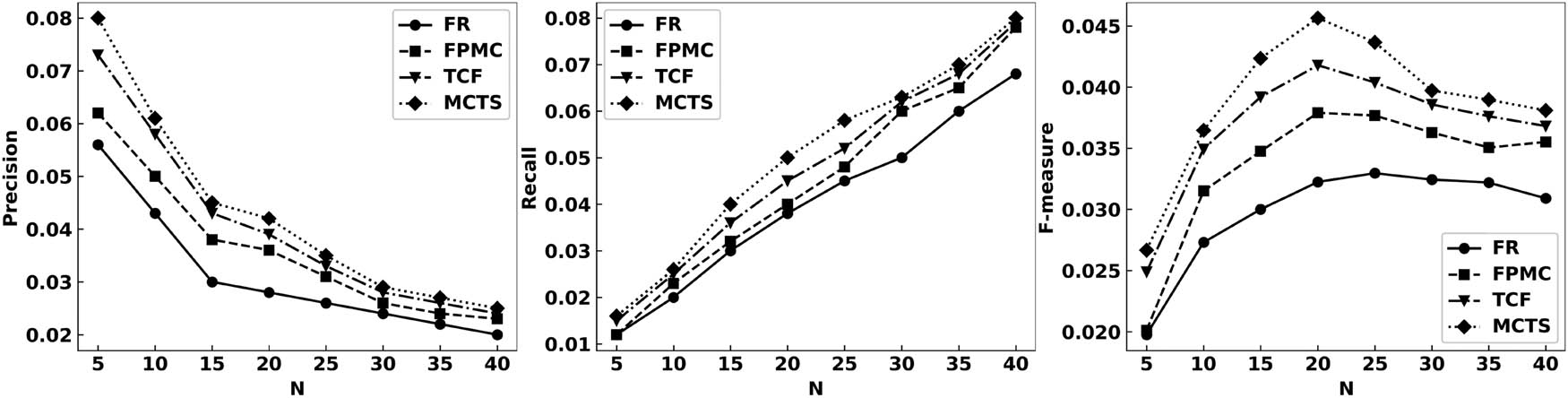
Each algorithm is based on the comparison of the precision, recall, and F-measure of the data of Movielens.

7 Conclusion

In this article, the ideas of Markov chains (MC) and collaborative filtering are cited. Traditional recommendation systems based on the Markov chain (MC) model can predict the next behavior of a user based on the user’s most recent behavior by continuous behavior data with time series attributes, and the continuous behavior of a user is modeled by the transfer matrix of the user’s preferred items. In this article, we use the Markov chain model to model the information, contained in users’ continuous behaviors through the transfer matrix of users’ preferences, so as to predict the set of labels preferred by users’ next behaviors based on the set of labels contained in the most recent behaviors. The items containing the set of user’s preferred labels are then analyzed for their attractiveness to the user. The tag frequency derived from the historical information can be used to calculate the user’s attraction to each tag in an item, which is aggregated into the user’s satisfaction with the item. However, this method only considers individual tags but ignores the interactions between tags. From the user’s perspective, the user’s satisfaction with a label is also influenced by the user’s satisfaction with other labels, so to a certain extent, labels can reinforce each other to improve the attractiveness to the user. If only independent tags are considered and the influence between tags is ignored, it will affect the recommendation effect. Therefore, it is necessary to consider the influence between tags when making Top-N recommendations

The experimental results show that the proposed social-based personalized recommendation algorithm is compared with three classical recommendation algorithms by applying two real datasets, Movielens, as the experimental platform. The experimental results show that the present recommendation algorithm has a certain degree of improvement in terms of accuracy and recall.

The Markov model used in this article is to consider the impact of continuous user behavior on recommendation, while the time factor is not considered in the group recommendation model, and the ternary relationship model and the time factor will be combined in the future to improve the effectiveness of recommendation. In addition, it will be our future research work to effectively model the relationship of multiple influences among tags to better reflect the influence of tags with different weights on Top-N recommendation results.

Conflict of interest: Authors state no conflict of interest.

References

[1] Li G, Wang S, Li ZY, Han ZY, Sun P, Sun HL. Personalized tag recommendation algorithm based on the tensor decomposition. Computer Sci. 2015;42(2):267–73.Search in Google Scholar

[2] Rendle S, Freudenthaler C, Schmidtthieme L. Factorizing personalized markov chains for next-basket recommendation. International Conference on World Wide Web. North Carolina, USA: ACM; 2010.10.1145/1772690.1772773Search in Google Scholar

[3] Li G, Wang S, Sun P, Han ZY, Li ZY, Sun HL. Recommendation algorithm based on personalized markov chains. Computer Sci. 2013;40(10):319–22.Search in Google Scholar

[4] Wen J, Yuan P, Zeng J, Wang XB, Zhou W. Research on collaborative filtering recommendation algorithm based on topic of tags. Computer Eng. 2017;43(1):247–52, 258.Search in Google Scholar

[5] Chen JM, Li JG, Tang FY, Tang Y, Chen XF, Tang TF. Combining user-item-tag tripartite graph and users personal interests for friends recommendation. J Front Computer Sci Technol. 2018;12(1):92–100.Search in Google Scholar

[6] Shani G, Heckerman D, Brafman RI. An MDP-Based Recommender system. J Mach Learn Res. 2005;6(1):1265–95.Search in Google Scholar

[7] Brin S, Page L. The anatomy of a large-scale hypertextual Web search engine. International Conference on World Wide Web. Brisbane, Australia: Elsevier Science Publishers B. V; 1998. p. 107–17.10.1016/S0169-7552(98)00110-XSearch in Google Scholar

[8] Hotho A, Jäschke R, Schmitz C, Stumme G. Information retrieval in folksonomies: search and ranking. Semantic Web Res Appl. 2006;4011:411–26.10.1007/11762256_31Search in Google Scholar

[9] Pham TAN, Li X, Cong G. A general model for out-of-town region recommendation. International Conference; 2017.10.1145/3038912.3052667Search in Google Scholar

[10] Liu J, Zhang K, Chen X. A personalized recommendation algorithm based on labeling and collaborative filtering. Computers Modern. 2016;2:62–5.Search in Google Scholar

[11] Cai Q, Han DM, Li HS, Hu YG, Chen Y. Personalized resource recommendation based on tagging and collaborative filtering. Computer Sci. 2014;41(1):69–71.Search in Google Scholar

[12] Li G, Chen ZX, Han ZY, Li ZY, Sun P. Personalized recommendation algorithm based on spectral clustering group discovery and Markov chains. Computer Sci. 2014;40(10):44–8.Search in Google Scholar

[13] Beckmann C, Gross T. AGReMo: Providing ad-hoc groups with on-demand recommendations on mobile devices. Proceedings of the 29th Annual European Conference on Cognitive Ergonomics. Rostock, Germany: ACM; 2011. p. 179–82.10.1145/2074712.2074747Search in Google Scholar

Received: 2022-02-21

Revised: 2022-04-05

Accepted: 2022-04-18

Published Online: 2022-06-14

This work is licensed under the Creative Commons Attribution 4.0 International License.