Pitagorasnon nga teyorema

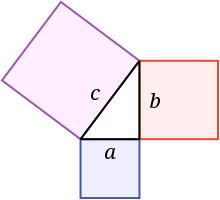
Ha matematika, an Pitagorasnon nga teyorema in uska relasyon ha Heyometriya Euclideanon ha tulo nga ligid han uska trayanggulo rectanggulo.

Mga reperensya

• Bell, John L. (1999). The Art of the Intelligible: An Elementary Survey of Mathematics in its Conceptual Development. Kluwer. ISBN 0-7923-5972-0. http://publish.uwo.ca/~jbell/. 
• Euclid (1956). Translated by Johan Ludvig Heiberg with an introduction and commentary by Sir Thomas L. Heath. ed. The Elements (3 vols.). Vol. 1 (Books I and II) (Reprint of 1908 ed.). Dover. ISBN 0-486-60088-2.  On-line text at Euclid
• Heath, Sir Thomas (1921). "The 'Theorem of Pythagoras'". A History of Greek Mathematics (2 Vols.) (Dover Publications, Inc. (1981) ed.). Clarendon Press, Oxford. p. 144 ff. ISBN 0-486-24073-8. http://books.google.com/?id=h4JsAAAAMAAJ&pg=PA144. 
• Libeskind, Shlomo (2008). Euclidean and transformational geometry: a deductive inquiry. Jones & Bartlett Learning. ISBN 0-7637-4366-6. http://books.google.com/books?id=6YUUeO-RjU0C&pg=PA41.  This high-school geometry text covers many of the topics in this WP article.
• Loomis, Elisha Scott (1968). The Pythagorean proposition (2nd ed.). The National Council of Teachers of Mathematics. ISBN 978-0-87353-036-1. https://archive.org/details/pythagoreanpropo0000loom_b2m3.  For full text of 2nd edition of 1940, see Elisha Scott Loomis. "The Pythagorean proposition: its demonstrations analyzed and classified, and bibliography of sources for data of the four kinds of proofs" (PDF). Education Resources Information Center. Institute of Education Sciences (IES) of the U.S. Department of Education. Ginkuhà 2010-05-04. Originally published in 1940 and reprinted in 1968 by National Council of Teachers of Mathematics, isbn=0-87353-036-5.
• Maor, Eli (2007). The Pythagorean Theorem: A 4,000-Year History. Princeton, New Jersey: Princeton University Press. ISBN 978-0-691-12526-8. http://books.google.com/?id=Z5VoBGy3AoAC&printsec=frontcover&q. 
• Stillwell, John (1989). Mathematics and Its History. Springer-Verlag. ISBN 0-387-96981-0. https://archive.org/details/mathematicsitshi0000stil.  Also ISBN 3-540-96981-0.
• Swetz, Frank; Kao, T. I. (1977). Was Pythagoras Chinese?: An Examination of Right Triangle Theory in Ancient China. Pennsylvania State University Press. ISBN 0-271-01238-2. https://archive.org/details/waspythagoraschi0000swet. 
• van der Waerden, Bartel Leendert (1983). Geometry and Algebra in Ancient Civilizations. Springer. ISBN 3-540-12159-5. http://books.google.com/?id=_vPuAAAAMAAJ&q=%22Pythagorean+triples%22++%22Babylonian+scribes%22+inauthor:van+inauthor:der+inauthor:Waerden&dq=%22Pythagorean+triples%22++%22Babylonian+scribes%22+inauthor:van+inauthor:der+inauthor:Waerden&cd=1. 

Mga sumpay ha gawas

• Pythagorean Theorem (more than 70 proofs from cut-the-knot)
• Interactive links:
  • Interactive proof in Java of The Pythagorean Theorem
  • Another interactive proof in Java of The Pythagorean Theorem
  • Pythagorean theorem with interactive animation
  • Animated, Non-Algebraic, and User-Paced Pythagorean Theorem
• History topic: Pythagoras's theorem in Babylonian mathematics Ginhipos 2011-06-06 han Wayback Machine
• Hazewinkel, Michiel, ed. (2001), "Pythagorean theorem", Encyclopedia of Mathematics, Springer, ISBN
• Batakan:MathWorld
• Euclid (David E. Joyce, ed. 1997) [c. 300 BC]. Elements. http://aleph0.clarku.edu/~djoyce/java/elements/toc.html. Ginkuhà 2006-08-30.  In HTML with Java-based interactive figures.