Eulerjev diagram

Eulerjev diagram je pripomoček, ki omogoča prikazovanje množic in njihovih odnosov. Prvo uporabo teh diagramov pripisujejo švicarskemu matematiku, fiziku in astronomu Leonhardu Eulerju (1707 – 1783). Nekateri jih imenujejo Eulerjevi krogi.

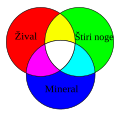
Diagrami so tesno povezani z Vennovimi diagrami. Eulerjevi diagrami so zgrajeni iz enostavnih zaprtih krivulj (običajno so to krogi), ki predstavljajo množice. Velikost in oblika krivulj nista pomembni. Pomembno pa je, kako se diagrami prekrivajo.

Vsaka Eulerjeva krivulja deli ravnino na dve področji. Prvo področje je notranje, ki predstavlja elemente množice. Drugo področje je zunanje, ki predstavlja vse elemente, ki niso elementi množice. Krivulje, katerih notranja področja se ne sekajo, predstavljajo disjunktno množico. Krivulje, katerih notranja področja se sekajo, predstavljajo množice, ki imajo skupne elemente. Krivulja, ki se nahaja v celoti, v notranjem področju drugega področja, se imenuje njena podmnožica.

Vennovi diagrami so bolj omejeni kot Eulerjevi diagrami. Vennovi diagrami morajo vsebovati vsa možna področja, ki se prekrivajo. V Eulerjevih diagramih pa lahko nekatera področja manjkajo.

Primeri majhnih Vennovih diagramov *(na levi)* z osenčenimi področji, ki predstavljajo prazne množice. To kaže na to, da se lahko brez težav pretvorijo v Eulerjeve diagrame *(desno)*.

Veitchov diagram in Karnaughov diagram kažeta minterme, toda Veitchov diagram ni primeren za zmanjševanje obrazcev. Obstoja močna podobnost med Vennovimi in Karnaughovimi diagrami, barve in spremenljivke x, y, in z so za primer Vennovega diagrama.

Zgledi Eulerjevih diagramov

Vennov diagram, ki kaže vse možne preseke.
Eulerjev diagram, ki kaže odnose med Mednarodnimi organizacijami v Afriki. Organizacije so zapisane s kraticami.
Diagram, ki primerja Eulerjev in Vennov diagram.
Eulerjev diagram vrst trikotnikov (predpostavlja se, da ima enakostraničen trikotnik najmanj 2 enaki stranici).
Eulerjev diagram za izraze povezane z Britanskim otočjem.

Zunanje povezave

Eulerjevi diagrami (angleško)
Diagrami (tudi Eulerjevi) (angleško)