Hiperbolična trigonometrija ima svoju ulogu u geometriji Lobačevskog . Koristi se za proučavanje otpornosti materijala , u elektrotehnici , statičkim proračunima visećih mostova u građevinarstvu i drugim granama nauke . U matematici se hiperbolične funkcije koriste, na primer, za rešavanje integrala gde se pojavljuje
√
(
1
+
x
2
)
,
{\displaystyle \surd (1+x^{2}),}
√
(
1
−
x
2
)
{\displaystyle \surd (1-x^{2})}
ravninska trigonometrija .
Hiperbolične funkcije je uveo u upotrebu italijanski matematičar Vinčenco Rikati (Vincenzo Riccati , 1707-1775). On je koristio oznake Sh. i Ch. za hiperbolni sinus i kosinus. Teoriju je dalje razvio Lambert (Johann Heinrich Lambert , 1728-1777. Histoire de l'académie Royale des sciences et des belles-lettres de Berlin , tom. XXIV, str. 327 (1768)), negde oko 1771, upotrebljavajući sinh i cosh. Kod nas se za hiperbolne funkcije koriste oznake sh x, ch x, th x, cth x, sech x, cosech x, ali ovde sledimo skraćenice koje podržava Vikipedijin softver, tj. Lateh , a to su uobičajene anglosaksonske oznake.
Sinus hiperbolični , kosinus hiperbolični i tangens hiperbolični određeni su formulama :
sinh
x
=
e
x
−
e
−
x
2
,
{\displaystyle \sinh x={\frac {e^{x}-e^{-x}}{2}},}
cosh
x
=
e
x
+
e
−
x
2
,
{\displaystyle \cosh x={\frac {e^{x}+e^{-x}}{2}},}
tanh
x
=
e
x
−
e
−
x
e
x
+
e
−
x
.
{\displaystyle \tanh x={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}.}
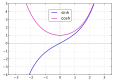
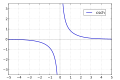
Sl.1. Graf sinusa hiperboličnog (plave boje, donji), i kosinus (crven, iznad)
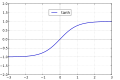
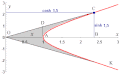
Sl.2. Graf tangensa hiperboličnog (plav)
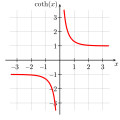
Sl.3. Graf kotangensa hiperboličnog (crven)
Kotangens hiperbolični , sekans hiperbolični i kosekans hiperbolični su recipročne vrednosti:
coth
x
=
1
tanh
x
=
e
x
+
e
−
x
e
x
−
e
−
x
,
{\displaystyle \coth x={\frac {1}{\tanh x}}={\frac {e^{x}+e^{-x}}{e^{x}-e^{-x}}},}
sech
x
=
1
cosh
x
=
2
e
x
+
e
−
x
,
{\displaystyle \operatorname {sech} x={\frac {1}{\cosh x}}={\frac {2}{e^{x}+e^{-x}}},}
csch
x
=
1
sinh
x
=
2
e
x
−
e
−
x
.
{\displaystyle \operatorname {csch} x={\frac {1}{\sinh x}}={\frac {2}{e^{x}-e^{-x}}}.}
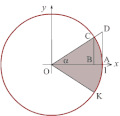
Geometrijsko određivanje hiperboličnih funkcija analogno je određivanju trigonometrijskih funkcija sinus , kosinus , tangens (v. ravninska trigonometrija ).
U trigonometrijskom krugu definisane su funkcije
sin
x
,
cos
x
,
tan
x
{\displaystyle \sin x,\;\cos x,\;\tan x}
ugao α je centralni ugao AOC. Isti ugao smo mogli definisati i kao površinu Pk dvostrukog kružnog isečka COK (sl.6. šrafirano).
Naime, kada je ugao AOC, tj. α u radijanima , tada dvostruki centralni isečak COK ima površinu
P
k
=
1
2
r
2
⋅
2
α
=
α
.
{\displaystyle P_{k}={\frac {1}{2}}r^{2}\cdot 2\alpha =\alpha .}
kružnicu
x
2
+
y
2
=
1
,
{\displaystyle x^{2}+y^{2}=1,}
hiperbolu
x
2
−
y
2
=
1
,
{\displaystyle x^{2}-y^{2}=1,}
P
h
=
x
{\displaystyle P_{h}=x}
Kada površinu h izračunamo (v. određeni integral ) dobijamo izraze za BC, OB, AD:
x
=
ln
(
B
C
+
B
C
2
+
1
)
=
ln
(
O
B
+
O
B
2
−
1
)
=
1
2
ln
1
+
A
D
1
−
A
D
,
{\displaystyle x=\ln(BC+{\sqrt {BC^{2}+1}})=\ln(OB+{\sqrt {OB^{2}-1}})={\frac {1}{2}}\ln {\frac {1+AD}{1-AD}},}
dakle za hiperbolne funkcije dobijamo prethodno navedene izraze u eksponencijalnom obliku:
B
C
=
e
x
−
e
−
x
2
=
sinh
x
,
{\displaystyle BC={\frac {e^{x}-e^{-x}}{2}}=\sinh x,}
O
B
=
e
x
+
e
−
x
2
=
cosh
x
,
{\displaystyle OB={\frac {e^{x}+e^{-x}}{2}}=\cosh x,}
A
D
=
e
x
−
e
−
x
e
x
+
e
−
x
=
tanh
x
.
{\displaystyle AD={\frac {e^{x}-e^{-x}}{e^{x}+e^{-x}}}=\tanh x.}
sin
z
=
−
i
sinh
z
,
sinh
z
=
−
i
sin
i
z
,
{\displaystyle \sin z=-i\sinh z,\quad \sinh z=-i\sin iz,}
cos
z
=
i
cosh
z
,
cosh
z
=
i
cos
i
z
,
{\displaystyle \cos z=i\cosh z,\quad \cosh z=i\cos iz,}
tan
z
=
−
i
tanh
z
,
tanh
z
=
−
i
tan
i
z
,
{\displaystyle \tan z=-i\tanh z,\quad \tanh z=-i\tan iz,}
cot
z
=
i
sinh
z
,
coth
z
=
i
cot
i
z
.
{\displaystyle \cot z=i\sinh z,\quad \coth z=i\cot iz.}
Svaka formula koja povezuje hiperbolične funkcije argumenta h ili ah, ali ne ax+b, može se dobiti iz odgovarajuće formule koja povezuje obične trigonometrijske funkcije ugla z zamenom
sin
z
{\displaystyle \sin z\,}
i
sinh
x
{\displaystyle i\sinh x\,}
cos
z
{\displaystyle \cos z\,}
cosh
x
.
{\displaystyle \cosh x.\,}
cos
2
z
+
sin
2
z
=
1
{\displaystyle \cos ^{2}z+\sin ^{2}z=1\,}
cosh
2
x
−
sinh
2
x
=
1
,
{\displaystyle \cosh ^{2}x-\sinh ^{2}x=1,\,}
sin
2
z
=
2
sin
y
cos
z
,
{\displaystyle \sin 2z=2\sin y\cos z,\,}
sinh
2
x
=
2
sinh
x
cosh
x
.
{\displaystyle \sinh 2x=2\sinh x\cosh x.\,}
Za hiperbolne funkcije vrede formule analogne formulama za funkcije obične trigonometrije .
cosh
2
x
−
sinh
2
x
=
1
,
sech
2
x
+
tanh
2
x
=
1
,
{\displaystyle \cosh ^{2}x-\sinh ^{2}x=1,\quad \operatorname {sech} ^{2}x+\tanh ^{2}x=1,}
coth
2
x
−
csch
2
x
=
1
,
tanh
x
⋅
coth
x
=
1
,
{\displaystyle \coth ^{2}x-\operatorname {csch} ^{2}x=1,\quad \tanh x\cdot \coth x=1,}
sinh
x
cosh
x
=
tanh
x
,
cosh
x
sinh
x
=
coth
x
.
{\displaystyle {\frac {\sinh x}{\cosh x}}=\tanh x,\quad {\frac {\cosh x}{\sinh x}}=\coth x.}
sinh
x
=
cosh
2
x
−
1
=
tanh
x
1
−
tan
2
x
=
1
coth
2
x
−
1
,
{\displaystyle \sinh x={\sqrt {\cosh ^{2}x-1}}={\frac {\tanh x}{\sqrt {1-\tan ^{2}x}}}={\frac {1}{\sqrt {\coth ^{2}x-1}}},}
cosh
x
=
sinh
2
x
+
1
=
1
1
−
tanh
2
x
=
coth
x
cot
2
x
−
1
,
{\displaystyle \cosh x={\sqrt {\sinh ^{2}x+1}}={\frac {1}{\sqrt {1-\tanh ^{2}x}}}={\frac {\coth x}{\sqrt {\cot ^{2}x-1}}},}
tanh
x
=
sinh
x
sinh
2
x
+
1
=
cosh
2
x
−
1
cosh
x
=
1
coth
x
,
{\displaystyle \tanh x={\frac {\sinh x}{\sqrt {\sinh ^{2}x+1}}}={\frac {\sqrt {\cosh ^{2}x-1}}{\cosh x}}={\frac {1}{\coth x}},}
coth
x
=
sinh
2
x
+
1
sinh
x
=
cosh
x
cosh
2
x
−
1
=
1
tanh
x
.
{\displaystyle \coth x={\frac {\sqrt {\sinh ^{2}x+1}}{\sinh x}}={\frac {\cosh x}{\sqrt {\cosh ^{2}x-1}}}={\frac {1}{\tanh x}}.}
sinh
(
x
±
y
)
=
sinh
x
cosh
y
±
cosh
x
sinh
y
,
{\displaystyle \sinh(x\pm y)=\sinh x\cosh y\pm \cosh x\sinh y,}
cosh
(
x
±
y
)
=
cosh
x
cosh
y
±
sinh
x
sinh
y
,
{\displaystyle \cosh(x\pm y)=\cosh x\cosh y\pm \sinh x\sinh y,}
tanh
(
x
±
y
)
=
tanh
x
±
tanh
y
1
±
tanh
x
tanh
y
,
coth
(
x
±
y
)
=
1
±
coth
x
coth
y
coth
x
±
coth
y
.
{\displaystyle \tanh(x\pm y)={\frac {\tanh x\pm \tanh y}{1\pm \tanh x\tanh y}},\quad \coth(x\pm y)={\frac {1\pm \coth x\coth y}{\coth x\pm \coth y}}.}
sinh
2
x
=
2
sinh
x
cosh
x
,
cosh
2
x
=
sinh
2
x
+
cosh
2
x
,
{\displaystyle \sinh 2x=2\sinh x\cosh x,\quad \cosh 2x=\sinh ^{2}x+\cosh ^{2}x,}
tanh
2
x
=
2
tanh
x
1
+
tanh
2
x
,
coth
2
x
=
1
+
coth
2
x
2
coth
x
.
{\displaystyle \tanh 2x={\frac {2\tanh x}{1+\tanh ^{2}x}},\quad \coth 2x={\frac {1+\coth ^{2}x}{2\coth x}}.}
(
cosh
x
±
sinh
x
)
n
=
cosh
n
x
±
sinh
n
x
{\displaystyle (\cosh x\pm \sinh x)^{n}=\cosh nx\pm \sinh nx}
sinh
x
2
=
±
cosh
x
−
1
2
,
{\displaystyle \sinh {\frac {x}{2}}=\pm {\sqrt {\frac {\cosh x-1}{2}}},}
cosh
x
2
=
cosh
x
+
1
2
,
{\displaystyle \cosh {\frac {x}{2}}={\sqrt {\frac {\cosh x+1}{2}}},}
tanh
x
2
=
cosh
x
−
1
sinh
x
=
sinh
x
cosh
x
+
1
,
coth
x
2
=
sinh
x
cosh
x
−
1
=
cosh
x
+
1
sinh
x
.
{\displaystyle \tanh {\frac {x}{2}}={\frac {\cosh x-1}{\sinh x}}={\frac {\sinh x}{\cosh x+1}},\quad \coth {\frac {x}{2}}={\frac {\sinh x}{\cosh x-1}}={\frac {\cosh x+1}{\sinh x}}.}
sinh
x
±
sinh
y
=
2
sinh
x
±
y
2
cosh
x
∓
y
2
,
{\displaystyle \sinh x\pm \sinh y=2\sinh {\frac {x\pm y}{2}}\cosh {\frac {x\mp y}{2}},}
cosh
x
+
cosh
y
=
2
cosh
x
+
y
2
cosh
x
−
y
2
,
{\displaystyle \cosh x+\cosh y=2\cosh {\frac {x+y}{2}}\cosh {\frac {x-y}{2}},}
cosh
x
−
cosh
y
=
2
sinh
x
+
y
2
sinh
x
−
y
2
,
{\displaystyle \cosh x-\cosh y=2\sinh {\frac {x+y}{2}}\sinh {\frac {x-y}{2}},}
tanh
x
±
tanh
y
=
sinh
(
x
±
y
)
cosh
x
cosh
y
.
{\displaystyle \tanh x\pm \tanh y={\frac {\sinh(x\pm y)}{\cosh x\cosh y}}.}
Nazivi area-sinus , area-kosinus , area-tangens i area-kotangens potiču od reči area (površina ) jer area-funkcije možemo predstaviti površinom hiperboličnog sektora. One su inverzne funkcijama sinus hiperbolni , kosinus hiperbolni , tangens hiperbolni i kotangens hiperbolni , tj. ako je
y
=
sinh
x
{\displaystyle y=\sinh x\,}
x
=
A
r
sinh
y
,
{\displaystyle x=Ar\sinh y,\,}
y
=
A
r
sinh
x
{\displaystyle y=Ar\sinh x\,}
area-sinus , ako je
x
=
sinh
y
,
{\displaystyle x=\sinh y,\,}
y
=
A
r
cosh
x
{\displaystyle y=Ar\cosh x\,}
area-kosinus , ako je
x
=
cosh
y
,
{\displaystyle x=\cosh y,\,}
y
=
A
r
tanh
x
{\displaystyle y=Ar\tanh x\,}
area-tangens , ako je
x
=
tanh
y
,
{\displaystyle x=\tanh y,\,}
y
=
A
r
coth
x
{\displaystyle y=Ar\coth x\,}
area-kotangens , ako je
x
=
coth
y
.
{\displaystyle x=\coth y.\,}
A
r
sinh
x
=
ln
(
x
+
x
2
+
1
)
,
{\displaystyle Ar\sinh x=\ln(x+{\sqrt {x^{2}+1}}),}
A
r
cosh
x
=
±
ln
(
x
+
x
2
−
1
)
,
x
≥
1
,
{\displaystyle Ar\cosh x=\pm \ln(x+{\sqrt {x^{2}-1}}),\;x\geq 1,}
A
r
tanh
x
=
1
2
ln
1
+
x
1
−
x
,
|
x
|
<
1
,
{\displaystyle Ar\tanh x={\frac {1}{2}}\ln {\frac {1+x}{1-x}},\;|x|<1,}
A
r
coth
x
=
1
2
ln
x
+
1
x
−
1
,
|
x
|
>
1.
{\displaystyle Ar\coth x={\frac {1}{2}}\ln {\frac {x+1}{x-1}},\;|x|>1.}
A
r
sinh
x
=
±
∗
A
r
cosh
x
2
+
1
=
A
r
tanh
x
x
2
+
1
=
A
r
coth
x
2
+
1
x
,
{\displaystyle Ar\sinh x=\pm ^{*}Ar\cosh {\sqrt {x^{2}+1}}=Ar\tanh {\frac {x}{\sqrt {x^{2}+1}}}=Ar\coth {\frac {\sqrt {x^{2}+1}}{x}},}
A
r
cosh
x
=
±
A
r
sinh
x
2
−
1
=
±
A
r
tanh
x
2
−
1
x
=
±
A
r
cosh
x
x
2
−
1
,
{\displaystyle Ar\cosh x=\pm Ar\sinh {\sqrt {x^{2}-1}}=\pm Ar\tanh {\frac {\sqrt {x^{2}-1}}{x}}=\pm Ar\cosh {\frac {x}{\sqrt {x^{2}-1}}},}
A
r
tanh
x
=
A
r
sinh
x
1
−
x
2
=
±
∗
A
r
cosh
1
1
−
x
2
=
A
r
coth
1
x
,
{\displaystyle Ar\tanh x=Ar\sinh {\frac {x}{\sqrt {1-x^{2}}}}=\pm ^{*}Ar\cosh {\frac {1}{\sqrt {1-x^{2}}}}=Ar\coth {\frac {1}{x}},}
A
r
coth
x
=
A
r
sinh
1
x
2
−
1
=
±
∗
A
r
cosh
x
x
2
−
1
=
A
r
tanh
1
x
.
{\displaystyle Ar\coth x=Ar\sinh {\frac {1}{\sqrt {x^{2}-1}}}=\pm ^{*}Ar\cosh {\frac {x}{\sqrt {x^{2}-1}}}=Ar\tanh {\frac {1}{x}}.}
Uz indeks * ide predznak + za h pozitivno, - za h negativno.
A
r
sinh
x
±
A
r
sinh
y
=
A
r
sinh
(
x
1
+
y
2
±
y
1
+
x
2
)
,
{\displaystyle Ar\sinh x\pm Ar\sinh y=Ar\sinh(x{\sqrt {1+y^{2}}}\pm y{\sqrt {1+x^{2}}}),}
A
r
cosh
x
±
A
r
cosh
y
=
A
r
cosh
(
x
y
±
(
x
2
−
1
)
(
y
2
−
1
)
)
,
{\displaystyle Ar\cosh x\pm Ar\cosh y=Ar\cosh(xy\pm {\sqrt {(x^{2}-1)(y^{2}-1)}}),}
A
r
tanh
x
±
A
r
tanh
y
=
A
r
tanh
x
±
y
1
±
x
y
.
{\displaystyle Ar\tanh x\pm Ar\tanh y=Ar\tanh {\frac {x\pm y}{1\pm xy}}.}
Sl.1. Graf sinusa hiperboličnog (plave boje, donji), i kosinus (crven, iznad)
Sl.2. Graf tangensa hiperboličnog (plav)
Sl.3. Graf kotangensa hiperboličnog (crven)
Sl.4. Graf sekansa hiperboličnog (crven)
Sl.5. Graf kosekansa hiperboličnog (plav)
Sl.6. Trigonometrijska kružnica
Sl.7. Trigonometrijska hiperbola
