JP6538624B2 - 信号処理装置、信号処理方法および信号処理プログラム - Google Patents

Description

本発明は、信号処理装置、信号処理方法および信号処理プログラムに関する。

従来、複数のマイクロホン等で観測した収録音を基に、当該音を発生させている音源の位置を推定する音源定位技術が知られている。音源定位技術として、例えば、音源数が既知であると仮定し、観測信号に時間周波数分析を適用することで推定した共分散行列を用いて音源位置を推定する方法が知られている。

R. O. Schmidt, "Multiple emitter location and signal parameter estimation," IEEE Transactions on Antennas and Propagation, 1986年3月, vol.AP-34, No.3, p.276-280. N. Ito, E. Vincent, N. Ono, R. Gribonval, and S. Sagayama, "Crystal-MUSIC:Accurate localization of multiple sources in diffuse noise environments using crystal-shaped microphone arrays," 2010年9月, Proceedings of 9th International Conference on Latent Variable Analysis and Signal Separation (LVA/ICA), p.81-88.

しかしながら、従来の音源定位技術には、観測信号長が短い場合に、音源定位を正確に行うことができない場合があるという問題があった。例えば、観測信号長が短い場合、共分散行列の推定のための十分な標本を得ることができず、音源定位を正確に行うことができないことがあった。

本発明の信号処理装置は、複数の異なる位置で取得された収録音に時間周波数分析を適用し、Ｍ次元ベクトルである観測信号ベクトルを計算する時間周波数分析部と、前記時間周波数分析部によって計算された観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルを、時間周波数点ごとに計算する特徴ベクトル計算部と、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、前記特徴ベクトルの条件付き確率分布のモデルパラメータを記憶するパラメータ記憶部と、前記音源位置を表す状態の事前確率分布を荷重とする、前記パラメータ記憶部に記憶されたモデルパラメータに基づく、前記音源位置を表す状態が既知の条件下での、前記特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、前記特徴ベクトル計算部によって計算された特徴ベクトルに当てはめ、前記事前確率分布を計算する事前確率分布計算部と、前記事前確率分布計算部によって計算された事前確率分布に基づいて、前記特徴ベクトルに対応する音源位置を計算する音源位置計算部と、を有することを特徴とする。

本発明の信号処理方法は、信号処理装置で実行される信号処理方法であって、複数の異なる位置で取得された収録音に時間周波数分析を適用し、Ｍ次元ベクトルである観測信号ベクトルを計算する時間周波数分析工程と、前記時間周波数分析工程によって計算された観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルを、時間周波数点ごとに計算する特徴ベクトル計算工程と、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、前記特徴ベクトルの条件付き確率分布のモデルパラメータを記憶するパラメータ記憶部に記憶されたモデルパラメータを取得し、前記音源位置を表す状態の事前確率分布を荷重とする、前記モデルパラメータに基づく、前記音源位置を表す状態が既知の条件下での、前記特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、前記特徴ベクトル計算工程によって計算された特徴ベクトルに当てはめ、前記事前確率分布を計算する事前確率分布計算工程と、前記事前確率分布計算工程によって計算された事前確率分布に基づいて、前記特徴ベクトルに対応する音源位置を計算する音源位置計算工程と、を含んだことを特徴とする。

本発明によれば、観測信号長が短い場合であっても、音源定位を正確に行うことができる。

図１は、本発明における音源定位について説明するための図である。 図２は、第１の実施形態に係る信号処理装置の構成の一例を示す図である。 図３は、第１の実施形態に係る信号処理装置の処理の流れを示すフローチャートである。 図４は、第８の実施形態に係る信号処理装置の構成の一例を示す図である。 図５は、第９の実施形態に係る信号処理装置の構成の一例を示す図である。 図６は、第１０の実施形態に係る信号処理装置の構成の一例を示す図である。 図７は、第１１の実施形態に係る信号処理装置の構成の一例を示す図である。 図８は、プログラムが実行されることにより信号処理装置が実現されるコンピュータの一例を示す図である。

以下に、本願に係る信号処理装置、信号処理方法および信号処理プログラムの実施形態を図面に基づいて詳細に説明する。なお、この実施形態により本発明が限定されるものではない。

［本発明における音源定位について］
音源信号は通常、時間周波数平面上の疎な点でのみ大きいパワーを持つというスパース性を持つため、複数の音源信号が同時に鳴っている状況でも、各時間周波数点では観測信号は音源信号のうち高々１つしか含まないとみなすことができる。そのため、例えば、Ｍ個（Ｍ＞１）の異なる位置で取得された観測信号の時間周波数変換からなるＭ次元縦ベクトルである観測信号ベクトルｙ（ｔ，ｆ）（ｔはフレームの番号（ｔ＝１〜Ｔ）、ｆは周波数ビンの番号（ｆ＝１〜Ｆ））は、当該時間周波数点（ｔ，ｆ）において観測信号に含まれる音源信号の音源位置によって定まる固有の方向を向いているとみなすことができる。正確には、雑音や残響の影響により、観測信号ベクトルｙ（ｔ，ｆ）の方向は、上記の音源位置によって定まる固有の方向を中心として多少の広がりを持って分布する。観測信号の上記の性質を利用すれば、観測信号ベクトルｙ（ｔ，ｆ）の方向に基づいて、音源位置を推定することができる。

本発明の実施形態では、音源定位を、複数（Ｌ個）の音源位置候補のうち、実際に音を発しているものを特定する問題、すなわち実際に音を発している音源位置候補（の番号）の集合を推定する問題として定式化する。この音源位置候補は、例えば、音源定位を行う部屋の中の複数の場所（例えば、部屋の中を格子状に細かく分割したときの各格子点に対応する場所）を音源位置候補とすることができる。また、音源位置候補は、音源が存在し得る領域が既知の場合には、その領域内の複数の場所を音源位置候補とすることができる。例えば、テーブルを囲んで座った複数人の会話の収録音に対し音源定位を行う場合、音源である話者はテーブルの外周付近にのみ存在しうるとみなせるから、テーブルの外周付近の複数の場所を音源位置候補とすることができる（図１参照）。そこで、観測信号の上記のような性質に基づき、本発明の実施形態では、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）の、音源位置を表す状態が複数（Ｌ個）の音源位置候補のそれぞれに対応する状態を取る条件下での条件付き確率分布のモデルパラメータを記憶しておき、当該モデルパラメータを事前情報として音源位置の推定に利用する。上述のように、観測信号ベクトルｙ（ｔ，ｆ）の方向は音源位置によって定まるとみなすことができるから、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）は音源位置によって定まる固有の確率分布を持つ。前記条件付き確率分布は、音源位置を表す状態が複数（Ｌ個）の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）の確率分布を表す。

観測信号ベクトルｙ（ｔ，ｆ）の方向とは、数学的には、観測信号ベクトルｙ（ｔ，ｆ）の全てのマイクロホンに対する要素比ｙ（１，ｔ，ｆ）：ｙ（２，ｔ，ｆ）：・・・：ｙ（Ｍ，ｔ，ｆ）を指す（言い換えれば、複素数体上のＭ次元ベクトル空間における互いにスカラ倍の関係にあるベクトルを同一視することにより得られる空間である、複素数体上のＭ−１次元射影空間の元を指す）。ここで、ｙ（ｍ，ｔ，ｆ）は、ベクトルｙ（ｔ，ｆ）の第ｍ要素を表す。したがって、特徴ベクトルｚ（ｔ，ｆ）が観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルであるとは、特徴ベクトルｚ（ｔ，ｆ）が与えられたときに観測信号ベクトルｙ（ｔ，ｆ）の全てのマイクロホンに対する要素比ｙ（１，ｔ，ｆ）：ｙ（２，ｔ，ｆ）：・・・：ｙ（Ｍ，ｔ，ｆ）が一意に定まることを意味する。前記観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルとしては、例えば観測信号ベクトルに平行な単位ベクトルを用いることができる。また、観測信号ベクトルｙ（ｔ，ｆ）自体も、当然観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んでいるから、これを観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルとして用いることもできる。観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルは、音源位置に関する情報として、位相差と振幅比の両方の情報を含んでいる。これは、振幅比を用いず位相差のみを用いる従来の特徴量（例えば、Time Difference of Arrival（TDOA）やDirection Of Arrival（DOA））と大きく異なる。そのため、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルは、振幅比を用いず位相差のみを用いる従来の特徴量と比較して、より多くの音源位置に関する情報を用いており、より正確な音源定位が可能である。また、限られたデータ長から音源位置に関する情報を最大限に抽出することができるため、本発明の実施形態において、観測信号長が短い場合であっても音源定位を正確に行うことができるという特長に貢献している。観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルを用いることで、位相差のみを用いる場合と比較して、より効果的な信号処理（例えば、音源分離や雑音除去）が可能であることが示されている（参考文献「H. Sawada, S. Araki, and S. Makino, “Underdetermined Convolutive Blind Source Separation via Frequency Bin-Wise Clustering and Permutation Alignment,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 19, no. 3, pp. 516-527, Mar. 2011. 」）。なお、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルが、音源位置に関する情報として、位相差と振幅比の両方の情報を含んでいるということは、下記のように説明できる。上述のように、観測信号ベクトルｙ（ｔ，ｆ）の方向とは観測信号ベクトルｙ（ｔ，ｆ）の全てのマイクロホンに対する要素比ｙ（１，ｔ，ｆ）：ｙ（２，ｔ，ｆ）：・・・：ｙ（Ｍ，ｔ，ｆ）を指すが、これは、全てのマイクロホン対（ｍ，ｎ）に対する、２つのマイクロホン（ｍ，ｎ）に対する要素比ｙ（ｍ，ｔ，ｆ）：ｙ（ｎ，ｔ，ｆ）と情報として等価である。さらに、複素数の比が位相差および絶対値の比（振幅比）と情報として等価であることに注意すると、全てのマイクロホン対（ｍ，ｎ）に対する、２つのマイクロホン（ｍ，ｎ）に対する要素比ｙ（ｍ，ｔ，ｆ）：ｙ（ｎ，ｔ，ｆ）は、全てのマイクロホン対（ｍ，ｎ）に対する、２つのマイクロホン（ｍ，ｎ）に対する位相差および振幅比と情報として等価である。したがって、観測信号ベクトルｙ（ｔ，ｆ）の方向は、全てのマイクロホン対（ｍ，ｎ）に対する、２つのマイクロホン（ｍ，ｎ）に対する位相差および振幅比と情報として等価である。すなわち、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルは、音源位置に関する情報として、位相差と振幅比の両方の情報を含んでいる。

図１を用いて、テーブルを囲んで座った複数人の会話の収録音に対し音源定位を行う場合の例について説明する。図１は、本発明における音源定位について説明するための図である。まず、図１に示すように、信号処理装置は、テーブル１００の周りの領域を等間隔に細かく分割したＬ点を音源位置候補１１０とすることができる。図１の例では、Ｌ＝８である。また、テーブル１００には、３つのマイクロホン１２０が置かれている。この例では、音源はテーブルの外周にのみ存在しうるとみなせ、また座高は個人に依らずほぼ一定とみなしうるから、音源位置はマイクロホン１２０から見た方向（方位角）によって指定することができる。

信号処理装置は、マイクロホン１２０によって観測された観測信号を基に、観測信号ベクトルｙ（ｔ，ｆ）および観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）を計算する。そして、信号処理装置は、条件付き確率分布のモデルパラメータに基づき、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布の荷重和である混合モデルを、特徴ベクトルｚ（ｔ，ｆ）に当てはめることにより、上記荷重和における荷重である事前確率分布を計算する。このとき、計算された事前確率分布は、音源位置で大きい値を取るため、この事前確率分布に基づいて音源位置を推定することができる。このとき、例えば、事前確率分布が、ｌ＝２である音源位置候補１１０で最も大きい値を取っている場合、音源位置は、矢印１３０が示す方向であるとみなすことができる。

［第１の実施形態］
第１の実施形態に係る信号処理装置は、音源数Ｎが未知の条件下で音源位置の集合を推定する。ここで、音源数ＮはＮ＝０であってもよい（音源位置の集合が空集合の場合に対応）。本実施形態では、信号処理装置は、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）として観測信号ベクトルｙ（ｔ，ｆ）の方向ベクトルを用い、音源位置を表す状態として複数の音源位置候補のそれぞれに対応する状態を用い、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布として複素ワトソン分布を用い、目的信号が球面波として伝播するという仮定に基づいて複素ワトソン分布のモデルパラメータを計算して記憶し、事前確率分布として時不変の事前確率分布を用いる。

図２を用いて、第１の実施形態に係る信号処理装置の構成について説明する。図２は、第１の実施形態に係る信号処理装置の構成の一例を示す図である。図２に示すように、信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。

時間周波数分析部１０は、複数の異なる位置で取得された収録音であるＭ個のマイクロホンによる観測信号ｙ（ｍ，τ）（ｍはマイクロホンの番号（ｍ＝１〜Ｍ）、τは時刻の番号）に時間周波数分析を適用して観測信号の時間周波数変換ｙ（ｍ，ｔ，ｆ）（ｔはフレームの番号（ｔ＝１〜Ｔ）、ｆは周波数ビンの番号（ｆ＝１〜Ｆ））を計算し、ｙ（ｍ，ｔ，ｆ）（ｍ＝１〜Ｍ）からなるＭ次元縦ベクトルである観測信号ベクトルｙ（ｔ，ｆ）を作成する。前記複数の異なる位置で取得された収録音は、複数の異なる位置で取得された後、何らかの前処理（例えば残響除去処理、空間的白色化処理など）が施された収録音でもよい（参考文献「T. Yoshioka, T. Nakatani, M. Miyoshi, and H. G. Okuno, “Blind separation and dereverberation of speech mixtures by joint optimization,” IEEE Trans. Audio, Speech, Language Process., vol. 19, no. 1, pp. 69-84, 2011.」、参考文献「H. Sawada, S. Araki, and S. Makino, “Underdetermined Convolutive Blind Source Separation via Frequency Bin-Wise Clustering and Permutation Alignment,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 19, no. 3, pp. 516-527, Mar. 2011. 」）。

特徴ベクトル計算部２０は、時間周波数分析部１０から観測信号ベクトルｙ（ｔ，ｆ）を受け取って、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）を式（１）により計算する。

ここで、||・||は、ユークリッドノルムであり、矢印←は左辺に右辺を代入することを表す。本実施形態におけるモデル化では、観測信号ベクトルｙ（ｔ，ｆ）はＮ個（Ｎは未知でもよく、またＮ＝０でもよい。）の目的信号からなり、背景雑音は含まないと仮定する。また、本発明の実施形態におけるモデル化では、各目的信号は時間周波数平面の疎な点でのみ大きいパワーを持つというスパース性を持つと仮定する。これらの仮定に基づき、本実施形態では、観測信号ベクトルｙ（ｔ，ｆ）は各時間周波数点において１つの目的信号のみを含むと仮定する。すなわち、観測信号ベクトルｙ（ｔ，ｆ）は式（２）によりモデル化される。

ここで、ｓ（ｎ，ｔ，ｆ）はｎ番目の目的信号の時間周波数変換であり、ｎは目的信号の番号（ｎ＝１〜Ｎ）である。また、ベクトルｈ（ｎ，ｆ）はｎ番目の目的信号の空間伝達特性を表すステアリングベクトルであり、ｎ番目の目的信号の音源位置によって固有の値を取る。式（２）は、観測信号ベクトルｙ（ｔ，ｆ）がｎ番目（ｎは時間周波数点（ｔ，ｆ）によって変化する）の目的信号のみからなることを表している。

観測信号ベクトルｙ（ｔ，ｆ）のＭ次元複素ベクトル空間における方向（すなわち、Ｍ次元複素ベクトル空間において観測信号ベクトルｙ（ｔ，ｆ）が張る１次元部分空間）は、当該時間周波数点（ｔ，ｆ）において観測信号に含まれる音源信号の音源位置によって定まる固有の方向（具体的にはステアリングベクトルｈ（ｎ，ｆ）の方向）となる。より正確には、雑音や残響の影響で、観測信号ベクトルｙ（ｔ，ｆ）の方向は、上記の音源位置によって定まる固有の方向を中心として多少の広がりを持って分布する。本実施形態では、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルとして、観測信号ベクトルｙ（ｔ，ｆ）の方向ベクトルである式（１）の特徴ベクトルを用いる。

本実施形態では、音源位置を表す状態が複数（Ｌ個）の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布を複素ワトソン分布によりモデル化する（他にも複素ビンガム分布、複素角度中心ガウス分布（complex angular central Gaussian distribution）、複素ガウス分布、混合複素ワトソン分布、混合複素ビンガム分布、混合複素角度中心ガウス分布、混合複素ガウス分布等の確率分布によりモデル化することができる）。すなわち、特徴ベクトルｚ（ｔ，ｆ）は式（３）によりモデル化される。

ここで、ｇ（ｔ，ｆ）は時間周波数点（ｔ，ｆ）における音源位置を表す状態である。本実施形態では、音源位置を表す状態は、複数（Ｌ個）の音源位置候補のそれぞれに対応する状態１〜Ｌのいずれかの値を取るとする。ここで、状態ｌは、時間周波数点（ｔ，ｆ）において観測信号ベクトルｙ（ｔ，ｆ）に含まれる音源信号の音源位置がｌ番目の音源位置候補である状態と定義する。ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）はｇ（ｔ，ｆ）＝ｌの条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である。ベクトルａ（ｌ，ｆ）はｌ番目の音源位置候補に対する特徴ベクトルｚ（ｔ，ｆ）の平均方向を定めるモデルパラメータであり、平均方向ベクトルと呼ばれ、式（４）を満たす。κ（ｌ，ｆ）はｌ番目の音源位置候補に対する特徴ベクトルｚ（ｔ，ｆ）の確率分布の平均方向ベクトルａ（ｌ，ｆ）のまわりへの集中度を定めるモデルパラメータであり、集中パラメータと呼ばれる。

Ｗ（ｚ；ａ，κ）は平均方向ベクトルがａ、集中パラメータがκであるベクトルｚの複素ワトソン分布であり、式（５）で表される。

このとき、Ｋは式（６）の無限級数により定義されるKummer関数（第１種合流型超幾何関数）であり、上付きのＨはエルミート転置である。ただし、ｉ＝０のときξ（ξ＋１）・・・（ξ＋ｉ−１）／［η（η＋１）・・・（η＋ｉ−１）］＝１と定める。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルの条件付き確率分布のモデルパラメータを記憶する。具体的に、パラメータ記憶部３０は、式（３）の条件付き確率分布の音源位置をモデル化するモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）および集中パラメータκ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）を記憶する。本実施形態では、これらのモデルパラメータを以下のように計算する。すなわち、目的信号が球面波として伝播するという仮定に基づき、平均方向ベクトルａ（ｌ，ｆ）の第ｍ要素を式（７）により計算する。

ここで、ベクトルｑ（ｍ）はｍ番目のマイクロホンの直交座標である３次元実ベクトル（本実施形態では既知と仮定）、ベクトルｒ（ｌ）はｌ番目の音源位置候補の直交座標である３次元実ベクトル（既知）、ｊは虚数単位、ω（ｆ）はｆ番目の周波数ビンの角周波数、ｃは音速であり、左辺における下付きのｍは第ｍ要素であることを表し、右辺の分母の平方根の項は、平均方向ベクトルａ（ｌ，ｆ）が式（４）の制約条件を満たすようにするための正規化係数である。

一方、集中パラメータκ（ｌ，ｆ）は、例えば周波数（ω（ｆ）／２π）のマイナス２乗に比例すると仮定して、式（８）により計算する。式（８）は、観測信号ベクトルｙ（ｔ，ｆ）の方向が、低い周波数ほど小さい分散（大きい集中度）を持つという性質に基づいている。このように、前記性質を適切に考慮することにより、事前確率分布の推定、及びそれに基づく音源定位を正確に行うことができる。比例定数βはどのように定めてもよいが、例えばβ＝６．４×１０＾７Ｈｚ＾２と定めればよい。

次に、本実施形態における特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布のモデル化について説明する。本実施形態では、特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布を、音源位置を表す状態ｇ（ｔ，ｆ）の事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）を荷重とする条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）の荷重和である、式（９）の混合モデルによりモデル化する。

条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）は音源位置を表す状態が既知の場合の特徴ベクトルｚ（ｔ，ｆ）の確率分布であるのに対し、式（９）の周辺確率分布ｐ（ｚ（ｔ，ｆ））は音源位置を表す状態が未知の場合の特徴ベクトルｚ（ｔ，ｆ）の確率分布である。事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）は、「時変」の場合と「時不変」の場合がある。前者の場合、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）は時間区間（例えばフレーム）ごとに異なる値を取り得る。後者の場合、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）は時間区間（例えばフレーム）によらず同一の値を取る。

事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）が時不変の場合、音源位置で大きい値を取る事前確率分布を全ての時間区間（例えばフレーム）を用いて推定することから、時変の場合よりも長いデータを推定に用いることができるため、音源の移動や発話交替がない状況では音源位置をより正確に推定できるという効果がある。その反面、音源位置推定を時間区間（例えばフレーム）ごとに行うことができず、またそのため、時変の場合の方が、音源の移動や発話交替がある動的な状況でのトラッキングやダイアリゼーション等には適している。

一方、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）が時変の場合、音源位置で大きい値を取る関数である事前確率分布を時間区間（例えばフレーム）ごとに推定するため、音源位置推定を時間区間（例えばフレーム）ごとに行うことができるという効果に加え、時間区間（例えばフレーム）ごとの音源位置推定に基づいてトラッキングやダイアリゼーションを行うことができるという効果がある。例えば、複数人会話の音声認識では、雑音を音声とみなして誤認識することを防ぐために、「いつ誰が話したか」を推定するダイアリゼーションを行うことで音声認識を適用すべき区間を切り出す必要があるが、「時変」の場合はこのような場合にも応用可能である。

本実施形態では、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）は時不変と仮定する。本実施形態では更に、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）は周波数にも依らないと仮定する。すなわち、本実施形態では、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）がフレームおよび周波数ビンに依存しないと仮定し、α（ｌ）で表す。ただし、α（ｌ）は制約条件α（１）＋…＋α（Ｌ）＝１を満たす。周波数に依らない事前確率分布を用いることで、全ての周波数において観測された特徴ベクトルｚ（ｔ，ｆ）の情報を用いて事前確率分布を推定することができるため、周波数に依存する事前確率分布を用いる場合と比べて、事前確率分布の推定により多くの情報を利用することができ、より正確な事前確率分布の推定およびそれに基づく音源定位が実現できるとともに、観測信号長が短い場合でもより正確な事前確率分布の推定およびそれに基づく音源定位が実現できる。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）と集中パラメータκ（ｌ，ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルに当てはめ、事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を計算する。

式（９）の混合モデルを特徴ベクトルｚ（ｔ，ｆ）に当てはめる方法には様々な方法があり、例えば式（９）に関する尤度を目的関数とし（他にも事後確率等を目的関数とすることができる。）、これを勾配法により事前確率分布α（ｌ）（ｌ＝１〜Ｌ）に関して最大化する（他にもＥｘｐｅｃｔａｔｉｏｎ−Ｍａｘｉｍｉｚａｔｉｏｎ（ＥＭ）アルゴリズム等により最大化できる）。

勾配法に基づく方法は、ＥＭアルゴリズムに基づく方法と比べて、計算量の面で有利である。ＥＭアルゴリズムに基づく方法では、反復ごとに、事前確率分布α（ｌ）（ｌ＝１〜Ｌ）に加えて、時間周波数点ごとの各音源位置候補の寄与率を計算する必要がある。これに対し、勾配法では、反復ごとに事前確率分布α（ｌ）（ｌ＝１〜Ｌ）のみを計算すれば良いため、ＥＭアルゴリズムに比べて計算量を大幅に削減することができる。事前確率分布計算部４０における処理は、例えば下記の通りである。

まず、α（ｌ）←１／Ｌ（ｌ＝１〜Ｌ）によりα（ｌ）を初期化する。次に、下記の式（１０）および（１１）によるα（ｌ）（ｌ＝１〜Ｌ）の処理を、交互に所定回数（例えば１０回）反復する。

そして、α（ｌ）（ｌ＝１〜Ｌ）を出力する。ただし、ベクトルαはα（ｌ）（ｌ＝１〜Ｌ）からなるＬ次元縦ベクトル、ベクトルｗ（ｔ，ｆ）はＷ（ｚ（ｔ，ｆ）；ａ（ｌ，ｆ），κ（ｌ，ｆ））（ｌ＝１〜Ｌ）からなるＬ次元縦ベクトル、上付きのＴは転置、λは所定の正の定数（例えばλ＝１）である。

ここで、式（１０）（１１）の導出について説明する。目的関数である尤度は、ｚ（ｔ，ｆ）（ｔ＝１〜Ｔ，ｆ＝１〜Ｆ）が観測される確率であり、式（１２）で表される。

式（１２）の最大化は、自然対数を取った式（１３）の最大化と等価である。

ここでｌｎは自然対数を表し、＝の上の△は定義であることを表す。式（１３）の勾配を取ると、式（１４）を得、これより式（１０）が従う。一方、式（１１）はα（ｌ）が制約条件α（１）＋…＋α（Ｌ）＝１を満たすようにするための処理である。なお、式（１３）において、荷重を用いずに和を取るのではなく、信頼度に基づく荷重を用いて荷重和を取るように変更した目的関数を用いてもよい。これにより、信頼度の高い時間周波数点における特徴ベクトルにより大きい重みを与えることができ、事前確率分布推定およびそれに基づく音源定位の精度を向上させることができる。例えば、観測信号ベクトルｙ（ｔ，ｆ）のノルムが小さい時間周波数点が雑音に対応し、前記ノルムが大きい時間周波数点が目的信号に対応するとの仮定に基づき、前記ノルムを信頼度に基づく荷重として用いることができる。

音源位置計算部５０は、事前確率分布計算部４０から事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を受け取って、事前確率分布α（ｌ）（ｌ＝１〜Ｌ）のピーク位置の集合Ｊを計算し、ピーク位置の集合Ｊに基づいて音源位置の集合Ｇを計算し出力する。

ピーク位置の集合Ｊは例えば次のように計算できる。各番号ｌ＝１〜Ｌに対し、ｌ番目の音源位置候補に隣接する音源位置候補の番号の集合が既知であると仮定する。このとき、「番号ｌがピーク位置であるとは、ｌ番目の音源位置候補に隣接する全ての音源位置候補の番号ｌ´に対しα（ｌ）＞α（ｌ´）が成り立つことである」と定義し、各番号ｌ＝１〜Ｌに対して番号ｌがピーク位置であるか否かを判定することで、ピーク位置の集合Ｊを計算できる。このピーク位置の集合Ｊに基づいて、音源位置を指定する番号ｌの集合または座標（直交座標、極座標、球座標等）の集合である検出された音源位置の集合Ｇを次のように計算できる。

例えば、ピーク位置の集合Ｊをそのまま検出された音源位置の集合Ｇとしてもよいし、ピーク位置ｌのうちピーク値α（ｌ）が所定の閾値Ｓを超えるピーク位置ｌの集合｛ｌ∈Ｊ｜α（ｌ）＞Ｓ｝を検出された音源位置の集合Ｇとしてもよい。閾値Ｓはどのように定めてもよいが、例えばＳ＝１／Ｌとすればよい。また、ピーク位置ｌに対応する音源位置候補の座標であるベクトルｒ（ｌ）の集合｛ｒ（ｌ）｜ｌ∈Ｊ｝を検出された音源位置の集合Ｇとしてもよいし、ピーク値α（ｌ）が所定の閾値Ｓを超えるピーク位置ｌに対応する音源位置候補の座標であるベクトルｒ（ｌ）の集合｛ｒ（ｌ）｜ｌ∈Ｊ，α（ｌ）＞Ｓ｝を検出された音源位置の集合Ｇとしてもよい。

［第１の実施形態の処理］
図３を用いて、信号処理装置１の処理の流れについて説明する。図３は、第１の実施形態に係る信号処理装置の処理の流れを示すフローチャートである。図３に示すように、まず、時間周波数分析部１０は、観測信号に対し、時間周波数分析を行い、観測信号ベクトルを計算する（ステップＳ１１）。

次に、特徴ベクトル計算部２０は、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルを計算する（ステップＳ１２）。そして、事前確率分布計算部４０は、パラメータ記憶部３０から、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルの条件付き確率分布モデルのパラメータを取得する（ステップＳ１３）。

次に、事前確率分布計算部４０は、各音源位置を表す状態の事前確率分布を初期化する（ステップＳ１４）。そして、事前確率分布計算部４０は、事前確率分布を更新する（ステップＳ１５）。

このとき、事前確率分布計算部４０は、例えば、パラメータ記憶部から取得したモデルパラメータによって表される特徴ベクトルの条件付き確率分布を、事前確率分布で荷重した混合モデルを用いて特徴ベクトルの周辺確率分布をモデル化する。そして、事前確率分布計算部４０は、勾配法を用い、当該周辺確率分布の尤度を目的関数としたときの尤度が最大化されるように事前確率分布を更新する。そして、事前確率分布の更新が所定回数反復して行われていない場合（ステップＳ１６、Ｎｏ）、事前確率分布計算部４０は、さらに事前確率分布の更新を行う（ステップＳ１５）。

一方、事前確率分布の更新が所定回数反復して行われた場合（ステップＳ１６、Ｙｅｓ）、音源位置計算部５０は、事前確率分布計算部４０によって計算された事前確率に基づいて音源位置を計算する（ステップＳ１７）。このとき、音源位置計算部５０は、例えば、事前確率がピークとなる音源位置を計算結果とすることができる。

［第１の実施形態の効果］
時間周波数分析部１０は、Ｍ個の異なる位置で取得された収録音に時間周波数変換を適用し、Ｍ次元ベクトルである観測信号ベクトルを計算する。そして、特徴ベクトル計算部２０は、時間周波数分析部１０によって計算された観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルを、時間周波数点ごとに計算する。また、パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルの条件付き確率分布のモデルパラメータを記憶する。

ここで、事前確率分布計算部４０は、音源位置を表す状態の事前確率分布を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータに基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルに当てはめ、事前確率分布を計算する。そして、音源位置計算部５０は、事前確率分布計算部４０によって計算された事前確率分布に基づいて、特徴ベクトルに対応する音源位置を計算する。

このように、第１の実施形態によれば、観測信号ベクトルの共分散行列を用いずに、音源位置にて大きい値を取る関数である空間スペクトルとみなせる事前確率分布を計算することができるため、観測信号長が短い場合でも正確に音源定位を行うことができる。そのため、観測信号長が短い場合に正確な音源定位が困難であったＣａｐоｎ法やＭＵＳＩＣ法等の従来の音源定位法に比べて、音源位置が時間的に変化する状況や、発話交替のある会話状況などの動的な状況下で有利である。また、第１の実施形態によれば、複数の音源からの音源信号が混在する状況でも、それぞれの音源の音源位置を推定することができる。そのため、複数の音源位置の推定が困難であった遅延和アレイや一般化相互相関関数法等の従来の音源定位法に比べて、発話の重なりがある会話状況などの複数音源が存在する状況下で有利である。また、音源数が未知である状況でも、音源定位を行うことができる。そのため、実際の応用では音源数は事前に分からないことが多いが、そのような状況下でも本実施形態により音源定位が可能である。これは、音源数の事前情報を必要とするＭＵＳＩＣ法等の従来の音源定位法に比べて有利である。さらに、第１の実施形態の方法で得られた事前確率分布は、トラッキング、ダイアリゼーション、マスク推定、音声強調、音声認識といった様々な応用に用いることができる。さらに、第１の実施形態によれば、周波数に依らない事前確率分布を用いることで、全ての周波数において観測された特徴ベクトルｚ（ｔ，ｆ）の情報を用いて事前確率分布を推定することができる（これは、式（１０）において、全ての周波数におけるベクトルｗ（ｔ，ｆ）を用いてベクトルαを更新していることからも分かる。）ため、周波数に依存する事前確率分布を用いる場合と比べて、事前確率分布の推定により多くの情報を利用することができ、より正確な事前確率分布の推定およびそれに基づく音源定位が実現できるとともに、観測信号長が短い場合でもより正確な事前確率分布の推定およびそれに基づく音源定位が実現できる。なお、上では、全てのフレームにおける観測信号を一度に処理するバッチ処理について説明したが、フレームごと（またはいくつかのフレームごと）に観測信号を処理し、音源位置を推定するブロックバッチ処理（またはオンライン処理）とすることもできる。

［第２の実施形態］
次に、第２の実施形態の構成について説明する。第２の実施形態は、本発明に基づいて音源位置を推定する例であり、第１の実施形態を基にして、事前確率分布として時変の事前確率分布を用いるという変更を加えたものである。すなわち、第２の実施形態では、事前確率分布を時間区間（例えばフレーム）ごとに推定する。このことにより、音源位置推定を時間区間（例えばフレーム）ごとに行うことができるという効果に加え、時間区間（例えばフレーム）ごとの音源位置推定に基づいてトラッキングやダイアリゼーションを行うことができるという効果が得られる。

第２の実施形態に係る信号処理装置の構成の一例は、第１の実施形態に係る信号処理装置１と同様、図２で示される。第２の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、およびパラメータ記憶部３０については、第１の実施形態と同様であるから、以下では相違点である事前確率分布計算部４０と音源位置計算部５０について詳しく説明する。第１の実施形態と本実施形態との主な相違点は次の通りである。第１の実施形態では、事前確率分布計算部４０で時間区間に依らない事前確率分布を計算し、この事前確率分布に基づき、音源位置計算部５０で時間区間に依らない音源位置を計算する。これに対し、本実施形態では、事前確率分布計算部４０で時間区間ごとの事前確率分布を計算し、この事前確率分布に基づき、音源位置計算部５０で時間区間ごとの音源位置を計算する。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）および集中パラメータκ（ｌ，ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布の荷重和である式（１５）の混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルｚ（ｔ，ｆ）に当てはめ、事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）を計算する。ただし、α（ｌ，ｔ）は制約条件α（１，ｔ）＋…＋α（Ｌ，ｔ）＝１を満たす。

ここで、第１の実施形態とは異なり、式（１５）における荷重が時不変のα（ｌ）ではなく時変のα（ｌ，ｔ）となっていることに注意する。式（１５）の混合モデルを特徴ベクトルｚ（ｔ，ｆ）に当てはめる方法には様々な方法があり、例えば式（１５）に関する尤度を勾配法により最大化する。

事前確率分布計算部４０における処理は、例えば下記の通りである。
１．α（ｌ，ｔ）←１／Ｌ（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）により事前確率分布α（ｌ，ｔ）を初期化する。
２．下記の式（１６）および式（１７）による事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）の更新を交互に所定回数（例えば１０回）反復する。

３．事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）を出力する。

ただし、ベクトルα（ｔ）はα（ｌ，ｔ）（ｌ＝１〜Ｌ）からなるＬ次元縦ベクトルである。式（１６）および（１７）の導出は、式（１０）および（１１）の導出と同様であるため省略する。

音源位置計算部５０は、事前確率分布計算部４０から事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）を受け取って、事前確率分布α（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）のピーク位置の集合Ｊ（ｔ）をフレームごとに計算し、ピーク位置の集合Ｊ（ｔ）に基づいて検出された音源位置の集合Ｇ（ｔ）をフレームごとに計算し出力する。

ピーク位置の集合Ｊ（ｔ）は例えば次のように計算できる。ｌ番目（ｌ＝１〜Ｌ）の音源位置候補に隣接する音源位置候補の番号の集合（既知と仮定）を集合Ａ（ｌ）で表す。このとき、ピーク位置の集合Ｊ（ｔ）は、「集合Ａ（ｌ）に属する全ての番号ｌ´に対しα（ｌ，ｔ）＞α（ｌ´，ｔ）」となる番号ｌの集合Ｊ（ｔ）＝｛ｌ｜∀ｌ´∈Ａ（ｌ），α（ｌ，ｔ）＞α（ｌ´，ｔ）｝として計算できる。このピーク位置の集合Ｊ（ｔ）に基づいて、音源位置を指定する番号ｌの集合または座標（直交座標、極座標、球座標等）の集合である検出された音源位置の集合Ｇ（ｔ）を次のように計算することができる。

例えば、ピーク位置の集合Ｊ（ｔ）をそのまま検出された音源位置の集合Ｇ（ｔ）とすることができる。また、ピーク位置ｌのうち対応するピーク値α（ｌ，ｔ）が所定の閾値Ｓを超えるものの集合｛ｌ∈Ｊ（ｔ）｜α（ｌ，ｔ）＞Ｓ｝を検出された音源位置の集合Ｇ（ｔ）とすることもできる。ここで閾値Ｓはどのように定めてもよいが、例えばＳ＝１／Ｌとすればよい。また、ピーク位置ｌに対応する音源位置候補の座標であるベクトルｒ（ｌ）の集合｛ｒ（ｌ）｜ｌ∈Ｊ（ｔ）｝を検出された音源位置の集合Ｇ（ｔ）とすることもできる。また、ピーク位置ｌのうちピーク値α（ｌ，ｔ）が所定の閾値Ｓを超えるものに対応する音源位置候補の座標であるベクトルｒ（ｌ）の集合｛ｒ（ｌ）｜ｌ∈Ｊ（ｔ），α（ｌ，ｔ）＞Ｓ｝を検出された音源位置の集合Ｇ（ｔ）としてもよい。

［第３の実施形態］
次に、第３の実施形態の構成について説明する。第３の実施形態は、本発明に基づいて音源位置を推定する例であり、第１の実施形態を基にして、音源位置を表す状態として、複数（Ｌ個）の音源位置候補のそれぞれに対応する状態（状態１〜Ｌとする）に加え、背景雑音に対応する状態（状態０とする）も考慮するとともに、音源位置を表す状態が状態０を取る条件下での、特徴ベクトルの条件付き確率分布を、超球面上の一様分布によりモデル化する、という変更を加えたものである。これにより、背景雑音を含む観測信号を適切にモデル化し、背景雑音下でも高精度に音源定位を行うことが可能になるという利点がある。

第３の実施形態に係る信号処理装置の構成の一例は、第１の実施形態に係る信号処理装置１と同様、図２で示される。第３の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０、特徴ベクトル計算部２０については、第１の実施形態と同様であるから、以下では相違点であるパラメータ記憶部３０、事前確率分布計算部４０、および音源位置計算部５０について詳しく説明する。第１の実施形態と本実施形態との主な相違点は次の通りである。第１の実施形態では、パラメータ記憶部３０において、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での条件付き確率分布のモデルパラメータを記憶し、事前確率分布計算部４０において、複数の音源位置候補に対応する状態に対する事前確率分布を計算し、音源位置計算部５０において、前記事前確率分布に基づいて音源位置を計算する。これに対し、本実施形態では、パラメータ記憶部３０において、音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータをさらに記憶し、事前確率分布計算部４０において、複数の音源位置候補および背景雑音に対応する状態の事前確率分布を計算し、音源位置計算部５０において、前記事前確率分布に基づいて音源位置を計算する。

まず、本実施形態における観測信号ベクトルｙ（ｔ，ｆ）のモデル化について説明する。本実施形態におけるモデル化では、観測信号ベクトルｙ（ｔ，ｆ）はＮ個（Ｎは未知でもよい。Ｎ＝０でもよい。）の目的信号に加えて背景雑音も含むと仮定する。本実施形態では更に、観測信号ベクトルｙ（ｔ，ｆ）は、各時間周波数点において目的信号のうち高々１つの目的信号を含むと仮定するとともに、背景雑音は全ての時間周波数点において観測信号ベクトルｙ（ｔ，ｆ）に含まれると仮定する。このとき、観測信号ベクトルｙ（ｔ，ｆ）は式（１８）または（１９）のいずれかの式によりモデル化される。

ここで、式（１８）は時間周波数点（ｔ，ｆ）において目的信号のうちｎ番目（ｎは時間周波数点（ｔ，ｆ）によって変化しうる）の目的信号のみが観測信号ベクトルｙ（ｔ，ｆ）に含まれる場合、式（１９）は時間周波数点（ｔ，ｆ）において観測信号ベクトルｙ（ｔ，ｆ）に目的信号が１つも含まれない場合を表しており、ベクトルｓ（ｎ，ｔ，ｆ）はｎ番目の目的信号、ベクトルｖ（ｔ，ｆ）は背景雑音である。

第１の実施形態の場合と異なり本実施形態では、式（１９）のように観測信号ベクトルｙ（ｔ，ｆ）に目的信号が１つも含まれず背景雑音のみが含まれる場合も考慮に入れたモデル化がなされており、背景雑音下での観測信号をより正確にモデル化することができる。

上述のように本実施形態では、式（１９）のように観測信号ベクトルｙ（ｔ，ｆ）に目的信号が１つも含まれない場合も考慮する。本実施形態では、このような場合も適切にモデル化できるように、各時間周波数点における観測信号ベクトルが取り得る音源位置を表す状態として、複数の音源位置候補に対応する状態に加えて、背景雑音に対応する状態をさらに考慮する。前者は式（１８）、後者は式（１９）に対応する。

以下、時間周波数点（ｔ，ｆ）における前記音源位置を表す状態をｇ（ｔ，ｆ）により表す。ｇ（ｔ，ｆ）＝ｌ（ｌ＝１〜Ｌ）の条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布は、第１の実施形態の場合と同様、式（３）の複素ワトソン分布によりモデル化される（他にも複素ビンガム分布、複素角度中心ガウス分布、複素ガウス分布、混合複素ワトソン分布、混合複素ビンガム分布、混合複素角度中心ガウス分布、混合複素ガウス分布等の確率分布によりモデル化することができる）。

一方、ｇ（ｔ，ｆ）＝０の条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布は、式（２０）に示すように、Ｍ次元複素ベクトル空間における単位球面上の一様分布によりモデル化される。

式（２０）は、背景雑音はあらゆる方向から一様に到来するという仮定に基づいている。本実施形態では、式（２０）を導入することにより、式（１９）のように背景雑音に対応する状態も適切にモデル化することが可能になり、背景雑音下でも音源位置を正確に推定できる。

次に、本実施形態における特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布のモデル化について説明する。本実施形態では、特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布を、音源位置を表す状態の事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）を荷重とする、条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）の荷重和である式（２１）の混合モデルによりモデル化する。

本実施形態では、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）がフレームおよび周波数ビンに依存しないと仮定し、α（ｌ）（ｌ＝０〜Ｌ）で表す。ただし、α（ｌ）は制約条件α（０）＋…＋α（Ｌ）＝１を満たす。κ＝０であり、ａが任意の単位ベクトルであるとき、複素ワトソン分布Ｗ（ｚ；ａ，κ）は式（２０）の一様分布に一致することに注意すると、式（２１）を式（２２）のように書き直すこともできる。ただし、κ（０，ｆ）＝０とし、ベクトルａ（０，ｆ）は任意の単位ベクトルとする。周波数に依らない事前確率分布を用いることで、全ての周波数において観測された特徴ベクトルｚ（ｔ，ｆ）の情報を用いて事前確率分布を推定することができるため、周波数に依存する事前確率分布を用いる場合と比べて、事前確率分布の推定により多くの情報を利用することができ、より正確な事前確率分布の推定およびそれに基づく音源定位が実現できるとともに、観測信号長が短い場合でもより正確な事前確率分布の推定およびそれに基づく音源定位が実現できる。さらに、全ての周波数において観測された特徴ベクトルｚ（ｔ，ｆ）の情報を用いて事前確率分布を推定することができるため、雑音や残響の影響により一つの周波数において観測された特徴ベクトルｚ（ｔ，ｆ）だけでは音源位置が確実には分からないような場合にも、より正確に音源定位を行うことができ、周波数に依存する事前確率分布を用いる場合と比べて、雑音や残響に対する頑健性を向上させることができる。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での条件付き確率分布のモデルパラメータ、および音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータを記憶する。前者は例えば第１の実施形態に記載の方法により計算することができ、後者は例えばκ（０，ｆ）←０、ベクトルａ（０，ｆ）は任意の単位ベクトルとすることができる。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布α（ｌ）（ｌ＝０〜Ｌ）を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）と集中パラメータκ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルの条件付き確率分布の荷重和である式（２１）の混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルｚ（ｔ，ｆ）に当てはめ、事前確率分布α（ｌ）（ｌ＝０〜Ｌ）を計算する。

式（２１）の混合モデルを特徴ベクトルｚ（ｔ，ｆ）に当てはめる方法には様々な方法があり、例えば式（２１）に関する尤度を目的関数とし（他にも事後確率等を目的関数とすることができる。）、これを勾配法により事前確率分布α（ｌ）（ｌ＝０〜Ｌ）に関して最大化する（他にもＥＭアルゴリズム等により最大化できる）。

事前確率分布計算部４０における処理は、例えば下記の通りである。
１．事前確率分布α（ｌ）（ｌ＝０〜Ｌ）をα（ｌ）←１／（Ｌ＋１）により初期化する。
２．下記の式（２３）および（２４）による事前確率分布α（ｌ）（ｌ＝０〜Ｌ）の更新を交互に所定回数（例えば１０回）反復する。

３．事前確率分布α（ｌ）（ｌ＝０〜Ｌ）を出力する。

ここで、ベクトル〜α（αの前の記号「〜」はαの上に記号「〜」を付すことを表す。）はα（ｌ）（ｌ＝０〜Ｌ）からなる（Ｌ＋１）次元縦ベクトルであり、ベクトル〜ｗ（ｔ，ｆ）はＷ（ｚ（ｔ，ｆ）；ａ（ｌ，ｆ），κ（ｌ，ｆ））（ｌ＝０〜Ｌ）からなる（Ｌ＋１）次元縦ベクトルである。なお、式（２３）および式（２４）の導出については、第１の実施形態と同様であるから省略する。

音源位置計算部５０は、事前確率分布計算部４０から受け取った事前確率分布α（ｌ）（ｌ＝０〜Ｌ）に基づいて、検出された音源位置の集合Ｇを計算し出力する。具体的には、ｌの定義域を目的音源に対応するｌ＝１〜Ｌに制限したα（ｌ）（ｌ＝１〜Ｌ）に対して、第１の実施形態に記載の処理を適用することにより、検出された音源位置の集合Ｇを計算する。

［第４の実施形態］
次に、第４の実施形態の構成について説明する。第４の実施形態は、本発明に基づいて音源位置を推定する例であり、第１の実施形態を基にして、条件付き確率分布のモデルパラメータを目的信号が球面波として伝播するという仮定に基づいて計算するのではなく、実測データを学習データとして用いて事前学習するようにするという変更を加えたものである。目的信号が球面波として伝播するという上記の仮定は、無響室のような反射・残響・回折等の存在しない理想的な環境を想定している。したがって、第１の実施形態では、反射・残響・回折等がある環境では、想定している環境と音源定位を行う環境との間にミスマッチが存在するため、音源定位の性能が低下する問題がある。これに対し本実施形態では、音源定位を行う環境における実測データを用いて条件付き確率分布のモデルパラメータを事前学習することで、そのようなミスマッチを解消し、反射・残響・回折等がある場合でも音源位置を正確に推定することが可能になる、という利点がある。反対に、第１の実施形態には、本実施形態と異なり上記実測データを取得する手間が省けるという利点がある。

第４の実施形態に係る信号処理装置の構成の一例は、第１の実施形態に係る信号処理装置１と同様、図２で示される。第４の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、事前確率分布計算部４０、および音源位置計算部５０については、第１の実施形態と同様であるから、以下では相違点であるパラメータ記憶部３０について詳しく説明する。第１の実施形態と本実施形態との主な相違点は次の通りである。第１の実施形態におけるパラメータ記憶部３０は、目的信号が球面波として伝播するという仮定に基づいて計算された、条件付き確率分布のモデルパラメータを記憶する。これに対し、本実施形態におけるパラメータ記憶部３０は、残響下で取得された学習データを用いて学習された、条件付き確率分布のモデルパラメータを記憶する。

パラメータ記憶部３０は、残響下で取得された学習データを用いて学習されたモデルパラメータであって、音源位置を表す状態が複数（Ｌ個）の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である複素ワトソン分布のモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）と集中パラメータκ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）を記憶する。前記残響下で取得された学習データとしては、例えば、背景雑音が存在しない状況で複数の音源位置候補のそれぞれからのみ音が発せられた場合の観測信号ｘ（ｌ，ｍ，τ）を用いることができる。

上記事前学習は、例えば次の手順で行うことができる。
１．１つの音源位置候補のみから音が発せられた場合の観測信号ｘ（ｌ，ｍ，τ）を生成する。例えば、Ｌ個の音源位置候補のそれぞれに対し、当該音源位置候補のみから音が発せられている状況で収録を行うことにより、ｘ（ｌ，ｍ，τ）を生成できる。もしくは、Ｌ個の音源位置候補のそれぞれに対し、当該音源位置候補から各マイクロホン位置までのインパルス応答を計測し、このインパルス応答を目的信号に畳み込むことにより、ｘ（ｌ，ｍ，τ）を生成できる。
２．ｘ（ｌ，ｍ，τ）の時間周波数変換ｘ（ｌ，ｍ，ｔ，ｆ）（ｍ＝１〜Ｍ）からなるＭ次元ベクトルｘ（ｌ，ｔ，ｆ）を計算する。
３．特徴ベクトルζ（ｌ，ｔ，ｆ）を下記の式（２５）により計算する。

４．特徴共分散行列Ｒ（ｌ，ｆ）を下記の式（２６）により計算する。

５．特徴共分散行列Ｒ（ｌ，ｆ）の固有値分解を行い、最大固有値μ（ｌ，ｆ）および最大固有値に対応するノルム１の固有ベクトルｅ（ｌ，ｆ）を求める。
６．平均方向ベクトルａ（ｌ，ｆ）をａ（ｌ，ｆ）←ｅ（ｌ，ｆ）とする。
７．集中パラメータκ（ｌ，ｆ）を下記の式（２７）により計算する。

上記の処理の導出について説明する。上記の処理は、特徴ベクトルζ（ｌ，ｔ，ｆ）が式（２８）に従って生成されるという仮定の下、式（２８）に関する対数尤度である式（２９）を平均方向ベクトルａ（ｌ，ｆ）および集中パラメータκ（ｌ，ｆ）に関して最大化することにより導かれる。

式（２９）において、平均方向ベクトルａ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）および集中パラメータκ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）のいずれにも依存しない定数項を無視すると、式（３０）のように書き直せる。

ここで、行列Ｒ（ｌ，ｆ）は式（２６）により定義される。式（２７）におけるベクトルａ（ｌ，ｆ）に依存する項は式（３１）である。

Courant-Fisherの定理より、式（３１）を式（４）の制約条件下で最大化するベクトルａ（ｌ，ｆ）は、特徴共分散行列Ｒ（ｌ，ｆ）の最大固有値μ（ｌ，ｆ）に対応するノルム１の固有ベクトルｅ（ｌ，ｆ）である。また、式（３０）における集中パラメータκ（ｌ，ｆ）に依存する項は、式（３２）である。

ここで、集中パラメータκ（ｌ，ｆ）に関する偏微分を０と置くと、式（３３）を得る。

参考文献１「S.Sra and D.Karp,"The multivariate Watson distribution: Maximum-likelihood estimation and other aspects," Journal of Multivariate Analysis,2013年2月,vol.114,p.256-269.」中の式（３．８）に基づいて、式（３３）を集中パラメータκ（ｌ，ｆ）について近似的に解くと式（２７）を得る。本実施形態では、学習データから集中パラメータを学習するため、第１の実施形態と同様、前述の、観測信号ベクトルｙ（ｔ，ｆ）の方向が、低い周波数ほど小さい分散（大きい集中度）を持つという性質を適切に考慮することができ、事前確率分布の推定、及びそれに基づく音源定位を正確に行うことができる。

［第５の実施形態］
次に、第５の実施形態の構成について説明する。第５の実施形態は、本発明に基づいて音源位置を推定する例であり、第３の実施形態を基にして、背景雑音に対する条件付き確率分布として一様分布を用いるのではなく、実測データを用いて事前学習した条件付き確率分布を用いるようにするという変更を加えたものである。

第３の実施形態における上記の一様分布の仮定は、雑音があらゆる方向から一様に到来する理想的な環境を想定している。したがって、第３の実施形態では、雑音の到来方向に偏りがある環境では、想定している環境と音源定位を行う環境との間にミスマッチが存在し、音源定位の性能が低下する恐れがある。これに対し本実施形態では、音源定位を行う環境における実測データを用いて、条件付き確率分布のモデルパラメータを事前学習することで、上記のミスマッチを解消し、雑音の到来方向に偏りがある場合でも音源位置を正確に推定することを可能にする、という利点がある。

第５の実施形態に係る信号処理装置の構成の一例は、第３の実施形態に係る信号処理装置１と同様、図２で示される。第５の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、事前確率分布計算部４０、および音源位置計算部５０については、第３の実施形態と同様であるから、以下では相違点であるパラメータ記憶部３０について詳しく説明する。第３の実施形態と本実施形態との主な相違点は次の通りである。第３の実施形態におけるパラメータ記憶部３０では、音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータとして、一様分布に対応するモデルパラメータを記憶する。これに対し、本実施形態におけるパラメータ記憶部３０では、音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータとして、学習データを用いて学習したモデルパラメータを記憶する。

本実施形態では、各時間周波数点における観測信号ベクトルｙ（ｔ，ｆ）の音源位置を表す状態がｇ（ｔ，ｆ）＝ｌ（ｌ＝０〜Ｌ）である条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布を、式（３）の複素ワトソン分布によりモデル化する（他にも複素ビンガム分布、複素角度中心ガウス分布、複素ガウス分布、混合複素ワトソン分布、混合複素ビンガム分布、混合複素角度中心ガウス分布、混合複素ガウス分布等の確率分布によりモデル化することができる）。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態（状態１〜Ｌ）を取る条件下での条件付き確率分布のモデルパラメータ、および音源位置を表す状態が背景雑音に対応する状態（状態０）を取る条件下での条件付き確率分布のモデルパラメータを記憶する。音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での条件付き確率分布のモデルパラメータは、例えば第１または第４の実施形態に記載の方法により計算することができる。

一方、音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータは、例えば次のように事前学習される。
１．実測した背景雑音ｘ（０，ｍ，τ）の時間周波数変換ｘ（０，ｍ，ｔ，ｆ）（ｍ＝１〜Ｍ）からなるＭ次元縦ベクトルｘ（０，ｔ，ｆ）を作成する。
２．特徴ベクトルζ（０，ｔ，ｆ）を次の式（３４）により計算する。

３．特徴共分散行列Ｒ（０，ｆ）を次の式（３５）により計算する。

４．特徴共分散行列Ｒ（０，ｆ）の固有値分解を行い、最大固有値μ（０，ｆ）および最大固有値に対応するノルム１の固有ベクトルｅ（０，ｆ）を求める。
５．平均方向ベクトルａ（０，ｆ）をａ（０，ｆ）←ｅ（０，ｆ）とする。
６．集中パラメータκ（０，ｆ）を次の式（３６）により計算する。

なお、上記の処理の導出は、第４の実施形態の場合と同様であるから省略する。

［第６の実施形態］
次に、第６の実施形態の構成について説明する。第６の実施形態は、本発明に基づいて音源位置を推定する例であり、第４の実施形態を基にして、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布として複素ワトソン分布ではなく複素角度中心ガウス分布を用いるようにするという変更を加えたものである。複素ワトソン分布では、観測信号ベクトルの方向である式（１）の特徴ベクトルの条件付き確率分布が回転対称である場合しか表せないのに対し、複素角度中心ガウス分布ではこの条件付き確率分布が回転対称な場合だけでなく楕円状の分布である場合も表すことができる。式（１）の特徴ベクトルの分布は必ずしも回転対称とは限らないため、本実施形態により、式（１）の特徴ベクトルの分布を第４の実施形態よりも正確にモデル化することができ、その結果、音源位置をより正確に推定できる。

第６の実施形態に係る信号処理装置の構成の一例は、第４の実施形態に係る信号処理装置１と同様、図２で示される。第６の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、および音源位置計算部５０については、第４の実施形態と同様であるから、以下では相違点であるパラメータ記憶部３０および事前確率分布計算部４０について詳しく説明する。第４の実施形態と本実施形態との主な相違点は次の通りである。第４の実施形態では、パラメータ記憶部３０において、条件付き確率分布をモデル化する複素ワトソン分布のモデルパラメータを記憶し、事前確率分布計算部４０において、前記複素ワトソン分布のモデルパラメータに基づいて事前確率分布を計算する。これに対し、本実施形態では、パラメータ記憶部３０において、条件付き確率分布をモデル化する複素角度中心ガウス分布のモデルパラメータを記憶し、事前確率分布計算部４０において、前記複素角度中心ガウス分布のモデルパラメータに基づいて事前確率分布を計算する。

本実施形態では、Ｌ個の音源位置候補に対するＬ個の条件付き確率分布を、複素角度中心ガウス分布によりモデル化する。すなわち、条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）を式（３７）によりモデル化する。

ここで、行列Σ（ｌ，ｆ）はｌ番目の音源位置候補に対する特徴ベクトルｚ（ｔ，ｆ）の分布の位置・広がり・方向・形状を定めるモデルパラメータである正定値エルミート行列であり、パラメータ行列と呼ばれ、Ａ（ｚ；Σ）は、パラメータ行列が行列Σであるベクトルｚの複素角度中心ガウス分布であり、式（３８）で表される。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である複素角度中心ガウス分布のモデルパラメータであるパラメータ行列Σ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）を記憶する。パラメータ行列Σ（ｌ，ｆ）は、Ｌ個の音源位置候補のそれぞれに対し、当該音源位置候補のみから音が発せられた場合の観測信号ｘ（ｌ，ｍ，τ）を用いて事前学習される。本実施形態では、特徴量ｚ（ｔ，ｆ）の条件付き確率分布の位置・広がり・方向・形状を定めるパラメータ行列Σ（ｌ，ｆ）を学習データから学習するため、第１の実施形態と同様、前述の、観測信号ベクトルｙ（ｔ，ｆ）の方向が、低い周波数ほど小さい分散（前記広がりに相当）を持つという性質を適切に考慮することができ、事前確率分布の推定、及びそれに基づく音源定位を正確に行うことができる。

この事前学習は、例えば以下の手順で行うことができる。
１．特徴ベクトルζ（ｌ，ｔ，ｆ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を第４の実施形態と同様に計算する。
２．パラメータ行列Σ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）をＭ×Ｍの単位行列により初期化する。
３．次の式（３９）によるパラメータ行列Σ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）の更新を所定回数（例えば１０回）反復する。

４．パラメータ行列Σ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）をパラメータ記憶部３０に記憶する。

式（３９）の導出について説明する。式（３９）は、特徴ベクトルζ（ｌ，ｔ，ｆ）が式（３７）の条件付き確率分布に従って生成されたという仮定の下、式（３７）に関する対数尤度である式（４０）をパラメータ行列Σ（ｌ，ｆ）に関して最大化することにより導かれる。

式（４０）におけるパラメータ行列Σ（ｌ，ｆ）によらない定数項を無視すると、式（４０）は、式（４１）のように書き換えられる。

式（４１）のパラメータ行列Σ（ｌ，ｆ）に関する偏微分を０と置いて整理すると、式（３９）を得る。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータであるパラメータ行列Σ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である複素角度中心ガウス分布の荷重和である混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルｚ（ｔ，ｆ）に当てはめ、事前確率分布を計算する。本実施形態では、前記事前確率分布として時不変の事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を考える。

事前確率分布計算部４０における事前確率分布の計算は、例えば次のように行えばよい。すなわち、ベクトルｗ（ｔ，ｆ）を条件付き確率である複素角度中心ガウス分布Ａ（ｚ（ｔ，ｆ）；Σ（ｌ，ｆ））（ｌ＝１〜Ｌ）からなるＬ次元縦ベクトルとし、ベクトルｗ（ｔ，ｆ）に対して第１の実施形態の事前確率分布計算部４０における処理を適用する。ただし、第１の実施形態とはベクトルｗ（ｔ，ｆ）の定義が異なることに注意する。なお、上記の処理の導出は、第１の実施形態の場合と同様であるから省略する。

［第７の実施形態］
次に、第７の実施形態の構成について説明する。第７の実施形態は、本発明に基づいて音源位置を推定する例であり、第４の実施形態を基にして、観測信号ベクトルｙ（ｔ，ｆ）の方向の情報を含んだベクトルである特徴ベクトルｚ（ｔ，ｆ）として式（１）の方向ベクトルではなく観測信号ベクトルｙ（ｔ，ｆ）そのものを用いるようにし、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布として複素ワトソン分布ではなく複素時変ガウス分布を用いるようにし、複素時変ガウス分布のモデルパラメータである空間共分散行列を事前学習して記憶するようにするという変更を加えたものである。

複素ワトソン分布では観測信号ベクトルの方向の分布が回転対称である場合しか表せないのに対し、複素時変ガウス分布では観測信号ベクトルの方向の分布が回転対称である場合だけでなく楕円状の分布である場合も表せる。観測信号ベクトルの方向の分布は必ずしも回転対称とは限らないため、本実施形態により、音源位置を特徴づける観測信号ベクトルの方向の分布を第４の実施形態よりも正確にモデル化することができ、このモデル化に基づき音源位置をより正確に推定できる。

第７の実施形態に係る信号処理装置の構成の一例は、第４の実施形態に係る信号処理装置１と同様、図２で示される。第７の実施形態に係る信号処理装置１は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０を有する。時間周波数分析部１０と音源位置計算部５０については第４の実施形態と同様であるから、以下では相違点である特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０について詳しく説明する。第４の実施形態と本実施形態との主な相違点は次の通りである。第４の実施形態では、特徴ベクトル計算部２０において式（１）の特徴ベクトルを計算し、パラメータ記憶部３０において、前記特徴ベクトルの条件付き確率分布をモデル化する複素ワトソン分布のモデルパラメータを記憶し、事前確率分布計算部４０において、音源位置を表す状態の事前確率分布を荷重とする、条件付き確率分布をモデル化する複素ワトソン分布の荷重和である混合モデルを前記特徴ベクトルに当てはめることにより、前記事前確率分布を計算する。これに対し、本実施形態では、特徴ベクトル計算部２０は、時間周波数分析部１０からの観測信号ベクトルを特徴ベクトルとして出力し、パラメータ記憶部３０において、特徴ベクトルである観測信号ベクトルの条件付き確率分布をモデル化する複素時変ガウス分布のモデルパラメータである空間共分散行列を記憶し、事前確率分布計算部４０において、音源位置を表す状態の事前確率分布を荷重とする、条件付き確率分布をモデル化する複素時変ガウス分布の荷重和である混合モデルを特徴ベクトルである観測信号ベクトルに当てはめることにより、前記事前確率分布を計算する。

特徴ベクトル計算部２０は、時間周波数分析部１０から観測信号ベクトルｙ（ｔ，ｆ）を受け取って、観測信号ベクトルｙ（ｔ，ｆ）を特徴ベクトルｚ（ｔ，ｆ）として出力する。

本実施形態では、Ｌ個の音源位置候補に対するＬ個の条件付き確率分布として、複素時変ガウス分布を用いる。すなわち、条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）を式（４２）によりモデル化する。

式（４２）におけるφ（ｌ，ｔ，ｆ）は、特徴ベクトルｚ（ｔ，ｆ）の「大きさ（ノルム）」の分布を制御する正のパラメータである。一方、式（４２）における行列Ｂ（ｌ，ｆ）は、特徴ベクトルｚ（ｔ，ｆ）の「方向」の分布を制御する（具体的には、特徴ベクトルｚ（ｔ，ｆ）の方向の分布の位置・広がり・方向・形状を制御する）パラメータである。行列Ｂ（ｌ，ｆ）は正定値エルミート行列であり、空間共分散行列と呼ばれる。Ｎ（ｚ；０，Φ）は平均がベクトル０、共分散行列が行列Φであるベクトルｚの複素ガウス分布であり、式（４３）で表される。

式（４２）は時変の共分散行列φ（ｌ，ｔ，ｆ）Ｂ（ｌ，ｆ）を持つことから、ここでは複素時変ガウス分布と呼ぶ。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）である観測信号ベクトルｙ（ｔ，ｆ）の条件付き確率分布のモデルパラメータである空間共分散行列Ｂ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）を記憶する。本実施形態では、パラメータ記憶部３０は、前記条件付き確率分布のモデルパラメータである空間共分散行列Ｂ（ｌ，ｆ）とφ（ｌ，ｔ，ｆ）のうち、音源位置に関係する空間共分散行列Ｂ（ｌ，ｆ）のみを記憶する。一方、φ（ｌ，ｔ，ｆ）は信号のパワーに依存するから、パラメータ記憶部３０には記憶せず、後で述べるように事前確率分布計算部４０において特徴ベクトル計算部２０からの特徴ベクトルを用いて推定する。本実施形態では、観測信号ベクトルｙ（ｔ，ｆ）の方向の分布の位置・広がり・方向・形状を定めるパラメータ行列Ｂ（ｌ，ｆ）を学習データから学習するため、第１の実施形態と同様、前述の観測信号ベクトルｙ（ｔ，ｆ）の方向が、低い周波数ほど小さい分散（前記広がりに相当）を持つという性質を適切に考慮することができ、事前確率分布の推定、及びそれに基づく音源定位を正確に行うことができる。

空間共分散行列Ｂ（ｌ，ｆ）は、Ｌ個の音源位置候補のうちの１つの音源位置候補のみから音が発せられた場合の観測信号ｘ（ｌ，ｍ，τ）を用いて、例えば以下の手順により事前学習される。
１．ｘ（ｌ，ｍ，τ）の時間周波数変換ｘ（ｌ，ｍ，ｔ，ｆ）（ｍ＝１〜Ｍ）からなるＭ次元縦ベクトルｘ（ｌ，ｔ，ｆ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を作成する。特徴ベクトルζ（ｌ，ｔ，ｆ）をζ（ｌ，ｔ，ｆ）←ｘ（ｌ，ｔ，ｆ）とする。ここで、特徴ベクトルζ（ｌ，ｔ，ｆ）の計算方法が、第４の実施形態とは異なることに注意する。
２．空間共分散行列Ｂ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）をＭ×Ｍの単位行列により初期化する。
３．次の式（４４）による空間共分散行列Ｂ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）の更新を所定回数（例えば１０回）反復する。

４．空間共分散行列Ｂ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）をパラメータ記憶部３０に記憶する。

式（４４）の導出について説明する。式（４４）は、ベクトルζ（ｌ，ｔ，ｆ）が式（４２）の条件付き確率分布に従って生成されたという仮定の下、式（４２）に関する対数尤度である式（４５）を空間相関行列Ｂ（ｌ，ｆ）およびφ（ｌ，ｔ，ｆ）に関して最大化することにより導かれる。

式（４５）における空間相関行列Ｂ（ｌ，ｆ）およびφ（ｌ，ｔ，ｆ）によらない定数項を無視すると、式（４５）は、式（４６）に書き換えられる。

式（４６）のφ（ｌ，ｔ，ｆ）に関する偏微分を０と置いて整理すると、式（４７）を得る。

また、式（４６）のＢ（ｌ，ｆ）に関する偏微分を０と置くと、式（４８）を得、式（４８）に式（４７）を代入すると式（４４）を得る。

次に、本実施形態における特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布のモデル化について説明する。本実施形態では、特徴ベクトルｚ（ｔ，ｆ）の周辺確率分布を、音源位置を表す状態ｇ（ｔ，ｆ）の事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）を荷重とする、条件付き確率分布ｐ（ｚ（ｔ，ｆ）｜ｇ（ｔ，ｆ）＝ｌ）の荷重和である式（４９）の混合モデルによりモデル化する。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータである空間相関行列Ｂ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布の荷重和である式（４９）の混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルｚ（ｔ，ｆ）に当てはめ、事前確率分布α（ｌ）（ｌ＝１〜Ｌ）を計算する。

式（４９）の混合モデルを特徴ベクトルｚ（ｔ，ｆ）に当てはめる方法には様々な方法があり、例えば式（４９）に関する尤度を目的関数とし（他にも事後確率等を目的関数とすることができる。）、これを勾配法に基づいて最大化する（他にもＥＭアルゴリズム等に基づいて最大化できる）。

事前確率分布計算部４０における事前確率分布α（ｌ）（ｌ＝１〜Ｌ）の推定は、第１の実施形態と同様にして行うことができる。ただし、第１の実施形態とは異なり、ベクトルｗ（ｔ，ｆ）を、Ｎ（ｚ（ｔ，ｆ），０，φ（ｌ，ｔ，ｆ）Ｂ（ｌ，ｆ））（ｌ＝１〜Ｌ）からなるＬ次元縦ベクトルとする。ここで、φ（ｌ，ｔ，ｆ）は次式により計算できる。

上記の処理の導出について説明する。目的関数である尤度は、特徴ベクトルｚ（ｔ，ｆ）（ｔ＝１〜Ｔ，ｆ＝１〜Ｆ）が観測される確率であり、式（５１）で表される。

式（５０）は式（５１）のφ（ｌ，ｔ，ｆ）に関する最大化により導かれる。式（５１）のφ（ｌ，ｔ，ｆ）に関する最大化は、ｌｎ［Ｎ（ｚ（ｔ，ｆ），０，φ（ｌ，ｔ，ｆ）Ｂ（ｌ，ｆ））］のφ（ｌ，ｔ，ｆ）に関する最大化と等価である。そこで、ｌｎ［Ｎ（ｚ（ｔ，ｆ），０，φ（ｌ，ｔ，ｆ）Ｂ（ｌ，ｆ））］のφ（ｌ，ｔ，ｆ）に関する偏微分を０とおくと、式（５０）を得る。あとは、第１の実施形態と同様にして、事前確率分布α（ｌ）（ｌ＝１〜Ｌ）の更新式である式（１０）および式（１１）を導出することができる。

［第８の実施形態］
次に、第８の実施形態の構成について説明する。第８の実施形態は、第２の実施形態に係る信号処理装置１により検出された音源位置の集合Ｇ（ｔ）を用いて、音源位置のトラッキングを行い、音源ごとフレームごとの音源位置ρ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ、Ｎは音源数）を計算する例である。本実施形態では音源位置が方位角のみで指定されるものとし、Ｇ（ｔ）は方位角の集合であり、ρ（ｎ，ｔ）は方位角であるとする。そのような状況としては、例えばマイクロホンが載っているテーブルを囲んで何人かが会話をしている状況が挙げられる。

図４を用いて、第８の実施形態に係る信号処理装置の構成について説明する。図４は、第８の実施形態に係る信号処理装置の構成の一例を示す図である。図４に示すように、信号処理装置２は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１を有する。時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０については、第２の実施形態と同様であるから、以下では相違点であるトラッキング部５１について詳しく説明する。

トラッキング部５１は、音源位置計算部５０からの検出された音源位置（方位角）の集合Ｇ（ｔ）（ｔ＝１〜Ｔ）を受け取り、音源位置のトラッキングを行って、音源ごとフレームごとの音源位置（方位角）ρ（ｎ，ｔ）（ｎ＝１〜Ｎ，ｔ＝１〜Ｔ）を計算し出力する。このトラッキングは様々な方法により行うことができる。以下ではその一例として、各音源の大まかな音源位置（方位角）が既知であると仮定し、これを利用してトラッキングを行う例を示す。各音源の大まかな音源位置（方位角）が既知である状況の例としては、マイクロホンが置かれた机を囲んで、複数人が椅子に座って会議をしている状況が挙げられる。この場合、椅子が既知の位置にほぼ固定されており、かつ会話中の話者の座席移動がないとすると、椅子の位置（既知）を各音源（話者）の大まかな音源位置として用いることができる。

まず、上記の各音源の大まかな音源位置を、音源位置（方位角）ρ（ｎ，ｔ）の初期値ρ（ｎ，０）とする。

フレームｔ−１での音源位置（方位角）ρ（ｎ，ｔ−１）が得られていると仮定すると、フレームｔでの音源位置（方位角）ρ（ｎ，ｔ）は、次の処理により求めることができる。
１．ρ（ｎ，ｔ）をρ（ｎ，ｔ）←ρ（ｎ，ｔ−１）により初期化する。
２．検出された音源位置（方位角）ｒ∈Ｇ（ｔ）（０≦ｒ＜２π）のそれぞれに対し、次の２−１および２−２の処理を行う。
２−１．次の式（５２）により、検出された音源位置（方位角）ｒに最も近い音源の番号νを計算する。

２−２．ν番目の音源の音源位置（方位角）ρ（ν，ｔ）を式（５３）により更新する。

式（５３）におけるｄ（ξ，η）は、式（５４）により定義される円周上の距離である。

また、式（５３）において、∠に下付きの［０，２π）を付した記号は、非零の複素数に対し［０，２π）の範囲の偏角を計算する演算子であり、∠に下付きの［−π，π）を付した記号は、非零の複素数に対し［−π，π）の範囲の偏角を計算する演算子であり、δは０＜δ＜１を満たす定数（例えばδ＝０．００５）である。

［第９の実施形態］
次に、第９の実施形態の構成について説明する。第９の実施形態は、第８の実施形態に係る信号処理装置２による処理結果に基づいて、ダイアリゼーション（diarization）を行う例である。このダイアリゼーションは、フレームごとに各音源が存在するか存在しないかを判定する（hard decision）ことによって行ってもよいし、フレームごとに各音源の存在確率を計算する（soft decision）ことによって行ってもよい。ここでは、前者の場合の例を示す。

図５を用いて、第９の実施形態に係る信号処理装置の構成について説明する。図５は、第９の実施形態に係る信号処理装置の構成の一例を示す図である。図５に示すように、信号処理装置３は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１、ダイアリゼーション部６０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１については、信号処理装置２と同様であるから、以下では相違点であるダイアリゼーション部６０について詳しく説明する。

ダイアリゼーション部６０は、音源位置計算部５０からの検出された音源位置の集合Ｇ（ｔ）（ｔ＝１〜Ｔ）と、トラッキング部５１からの音源ごとフレームごとの音源位置（方位角）ρ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）とを受け取って、音源ごとフレームごとのダイアリゼーション結果ｄ（ｎ，ｔ）を計算し出力する。ただし、フレームｔで音源ｎが存在するときｄ（ｎ，ｔ）＝１、フレームｔで音源ｎが存在しないときｄ（ｎ，ｔ）＝０と定める。

ダイアリゼーション結果ｄ（ｎ，ｔ）の計算方法としては様々な方法が考えられるが、例えば次のように計算すればよい。
１．ｄ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）をｄ（ｎ，ｔ）←０により初期化する。
２．ｔ＝１〜Ｔに対して次の処理を行う：検出された音源位置（方位角）ｒ∈Ｇ（ｔ）のそれぞれに対し、距離ｄ（ｒ，ρ（ｎ，ｔ））が最小となる音源番号ｎであるνを求め、ｄ（ν，ｔ）←１とする。
３．ｄ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）をダイアリゼーション結果とする。

なお、第９の実施形態において、各音源の正確な音源位置（方位角）が既知の状況では、トラッキング部５１で計算された音源位置（方位角）を用いる代わりに、既知の音源位置（方位角）を音源ごとフレームごとの音源位置（方位角）ρ（ｎ，ｔ）として用いてもよい。そのような状況としては例えば、話者が固定された椅子に座って会話をしている状況や、ビデオカメラの映像により音源位置（方位角）が分かっている状況等がある。

［第１０の実施形態］
次に、第１０の実施形態の構成について説明する。第１０の実施形態は、背景雑音下でＮ個（Ｎ＞０）の目的信号が混在する状況において、本発明により推定した音源位置に基づいて各目的信号の波形を推定する例である。本実施形態により、混ざった目的信号を個々の目的信号に分離するとともに、背景雑音を除去することができる。

図６を用いて、第１０の実施形態に係る信号処理装置の構成について説明する。図６は、第１０の実施形態に係る信号処理装置の構成の一例を示す図である。図６に示すように、信号処理装置４は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１、ダイアリゼーション部６０、マスク推定部７０、信号強調部８０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、トラッキング部５１、およびダイアリゼーション部６０については信号処理装置３と同様であるから、以下では相違点であるパラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、マスク推定部７０、信号強調部８０について詳しく説明する。信号処理装置３と信号処理装置４の主な相違点は次の通りである。信号処理装置３では、パラメータ記憶部３０において、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での条件付き確率分布のモデルパラメータを記憶し、事前確率分布計算部４０において、前記モデルパラメータに基づいて複数の音源位置候補に対応する状態の事前確率分布を計算し、音源位置計算部５０において、前記事前確率分布に基づいて音源位置を計算する。これに対し、信号処理装置４では、パラメータ記憶部３０において、音源位置を表す状態が背景雑音に対応する状態を取る条件下での条件付き確率分布のモデルパラメータをさらに記憶し、事前確率分布計算部４０において、前記モデルパラメータに基づいて複数の音源位置候補および背景雑音に対応する状態の事前確率分布を計算し、音源位置計算部５０において、前記事前確率分布に基づいて音源位置を計算する。信号処理装置４では更に、マスク推定部７０において、各目的信号および背景雑音の時間周波数点ごとの寄与度（事後確率）であるマスクを推定し、信号強調部８０において、前記マスクに基づいて各目的信号の波形を計算する。

パラメータ記憶部３０は、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である複素ワトソン分布のモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）と集中パラメータκ（ｌ，ｆ）（ｌ＝１〜Ｌ、ｆ＝１〜Ｆ）、および音源位置を表す状態が背景雑音に対応する状態を取る条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布である複素ワトソン分布のモデルパラメータである平均方向ベクトルａ（０，ｆ）（ｆ＝１〜Ｆ）と集中パラメータκ（０，ｆ）（ｆ＝１〜Ｆ）を記憶する。これらのモデルパラメータは、音源位置候補のそれぞれに対応する状態に対しては例えば第４の実施形態に記載の方法により計算でき、背景雑音に対応する状態に対しては例えば第３の実施形態に記載の方法により計算できる。

事前確率分布計算部４０は、音源位置を表す状態の事前確率分布を荷重とする、パラメータ記憶部３０に記憶されたモデルパラメータである平均方向ベクトルａ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）と集中パラメータκ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）に基づく、音源位置を表す状態が既知の条件下での、特徴ベクトルｚ（ｔ，ｆ）の条件付き確率分布の荷重和である式（２１）の混合モデルを、特徴ベクトル計算部２０によって計算された特徴ベクトルｚ（ｔ，ｆ）に当てはめ、事前確率分布を計算する。本実施形態では、事前確率分布Ｐ（ｇ（ｔ，ｆ）＝ｌ）がフレームに依存すると仮定し、α（ｌ，ｔ）（ｌ＝０〜Ｌ，ｔ＝１〜Ｔ）で表す。α（ｌ，ｔ）は制約条件α（０，ｔ）＋…＋α（Ｌ，ｔ）＝１を満たす。式（２１）の混合モデルを特徴ベクトルｚ（ｔ，ｆ）に当てはめる方法には様々な方法があるが、本実施形態では式（２１）に関する尤度を勾配法により事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）に関して最大化することにより行う。

事前確率分布計算部４０における処理は、例えば下記の通りである。
１．事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）をα（ｌ，ｔ）←１／（Ｌ＋１）により初期化する。
２．次の式（５５）および式（５６）による事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）の更新を交互に所定回数（例えば１０回）反復する。

３．事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）を出力する。

ここで、ベクトル〜α（ｔ）（αの前の記号「〜」はαの上に記号「〜」を付すことを表す。）はα（ｌ，ｔ）（ｌ＝０〜Ｌ）からなる（Ｌ＋１）次元縦ベクトルであり、ベクトル〜ｗ（ｔ，ｆ）はＷ（ｚ（ｔ，ｆ）；ａ（ｌ，ｆ），κ（ｌ，ｆ））（ｌ＝０〜Ｌ）からなる（Ｌ＋１）次元縦ベクトルである。なお、式（５５）および式（５６）の導出については、第１の実施形態の場合と同様であるから省略する。

音源位置計算部５０は、事前確率分布計算部４０から受け取った事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）に基づいて、検出された音源位置の集合Ｇ（ｔ）（ｔ＝１〜Ｔ）を計算し出力する。具体的には、事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）の定義域を目的音源に対応するｌ＝１〜Ｌに制限したα（ｌ，ｔ）（ｌ＝１〜Ｌ、ｔ＝１〜Ｔ）に対して、第２の実施形態の音源位置計算部５０における処理を適用することにより、検出された音源位置の集合Ｇ（ｔ）（ｔ＝１〜Ｔ）を計算する。

マスク推定部７０は、パラメータ記憶部３０からの平均方向ベクトルａ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）と集中パラメータκ（ｌ，ｆ）（ｌ＝０〜Ｌ、ｆ＝１〜Ｆ）、事前確率分布計算部４０からの事前確率分布α（ｌ，ｔ）（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ）、およびトラッキング部５１からの音源ごとフレームごとの音源位置（方位角）ρ（ｎ，ｔ）（ｎ＝１〜Ｎ，ｔ＝１〜Ｔ）を受け取って、特徴ベクトルｚ（ｔ，ｆ）に対する背景雑音および各目的信号の時間周波数点ごとの寄与度（事後確率）であるマスクγ（ｎ，ｔ，ｆ）（ｎ＝０〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を計算し出力する。ここで、γ（０，ｔ，ｆ）は背景雑音に対応するマスクであり、γ（ｎ，ｔ，ｆ）（ｎ＝１〜Ｎ）は目的信号ｎに対応するマスクである。

マスクγ（ｎ，ｔ，ｆ）は様々な方法により計算することができるが、例えば以下のように計算する。
１．特徴ベクトルｚ（ｔ，ｆ）が与えられた条件下でｇ（ｔ，ｆ）＝ｌとなる事後確率Ｐ（ｇ（ｔ，ｆ）＝ｌ｜ｚ（ｔ，ｆ））（ｌ＝０〜Ｌ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を次の式（５７）および式（５８）により計算する。

２．背景雑音に対応するマスクγ（０，ｔ，ｆ）（ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を次の式（５９）により計算する。

３．フレームｔにおいて各目的信号ｎに対応する音源位置候補の番号ｌの集合Ｊ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）を次の式（６０）により計算する。

４．目的信号に対応するマスクγ（ｎ，ｔ，ｆ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を次の式（６１）により計算する。

５．マスクγ（ｎ，ｔ，ｆ）（ｎ＝０〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を出力する。

信号強調部８０は、時間周波数分析部１０からの観測信号ベクトルｙ（ｔ，ｆ）、ダイアリゼーション部６０からの０または１のいずれかの値を取るダイアリゼーション結果ｄ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）、およびマスク推定部７０からの背景雑音および各目的信号のマスクγ（ｎ，ｔ，ｆ）（ｎ＝０〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を受け取って、各目的信号ｓ（ｎ，τ）を推定する。

信号強調部８０における具体的な処理の例は以下の通りである。
１．観測信号の共分散行列Φ（ｆ）を次の式（６２）により計算する。

２．ダイアリゼーション結果ｄ（ｎ，ｔ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ）を用いて修正したマスク〜γ（ｎ，ｔ，ｆ）（ｎ＝０〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を次の式（６３）および式（６４）により計算する。式（６３）は、ｄ（ｎ，ｔ）＝０のときにはフレームｔにおける音源ｎのマスクを０で置き換えることを意味している。また、式（６４）は、マスク〜γ（ｎ，ｔ，ｆ）のｎに関する総和が１になるようにするための処理である。

３．共分散行列Ψ（ｎ，ｆ）（ｎ＝０〜Ｎ、ｆ＝１〜Ｆ）を次の式（６５）により計算する。ここで、行列Ψ（０，ｆ）は背景雑音に対応する共分散行列であり、行列Ψ（ｎ，ｆ）（ｎ＝１〜Ｎ）はｎ番目の目的信号と背景雑音の和に対応する共分散行列である。

４．ｎ番目の目的信号と背景雑音の和に対応する共分散行列Ψ（ｎ，ｆ）から背景雑音に対応する共分散行列Ψ（０，ｆ）を減算することにより、ｎ番目の目的信号に対応する共分散行列〜Ψ（ｎ，ｆ）（ｎ＝１〜Ｎ、ｆ＝１〜Ｆ）を求める。次に、各目的信号のステアリングベクトルｈ（ｎ，ｆ）（ｎ＝１〜Ｎ、ｆ＝１〜Ｆ）を、行列〜Ψ（ｎ，ｆ）の最大固有値に対応する固有ベクトルとして求める。そして、ベクトルｈ（ｎ，ｆ）の第１要素が１に等しくなるように、ｈ（ｎ，ｆ）←ｈ（ｎ，ｆ）／ｈ（１，ｎ，ｆ）によりベクトルｈ（ｎ，ｆ）を正規化する。ここで、ｈ（１，ｎ，ｆ）はベクトルｈ（ｎ，ｆ）の第１要素を表す。

５．最小分散ビームフォーマに基づき、各目的信号の時間周波数変換ｓ（ｎ，ｔ，ｆ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）を次の式（６７）により計算する。

６．各目的信号の時間周波数変換ｓ（ｎ，ｔ，ｆ）（ｎ＝１〜Ｎ、ｔ＝１〜Ｔ、ｆ＝１〜Ｆ）に時間周波数変換の逆変換を適用することにより、各目的信号ｓ（ｎ，τ）を計算する。

［第１１の実施形態］
次に、第１１の実施形態の構成について説明する。第１１の実施形態は、背景雑音下でＮ個（Ｎ＞０）の目的音声が存在する状況において、本発明により推定した音源位置に基づいて各目的音声の波形を推定し、各目的音声に対して既存の音声認識技術を適用することで各目的音声を音声認識する例である。本発明によれば、背景雑音や複数の話者による音声が混在した状況でも、混ざった目的信号を個々の目的信号に分離するとともに、背景雑音を除去し、高精度な音声認識を実現できる。応用例としては、例えば様々な音が鳴っているオフィスの片隅で行われた会議の自動書き起こし等が挙げられる。

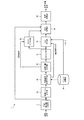
図７を用いて、第１１の実施形態に係る信号処理装置の構成について説明する。図７は、第１１の実施形態に係る信号処理装置の構成の一例を示す図である。図７に示すように、信号処理装置５は、時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１、ダイアリゼーション部６０、マスク推定部７０、信号強調部８０、音声認識部９０を有する。時間周波数分析部１０、特徴ベクトル計算部２０、パラメータ記憶部３０、事前確率分布計算部４０、音源位置計算部５０、トラッキング部５１、ダイアリゼーション部６０、マスク推定部７０、信号強調部８０については第１０の実施形態と同様である。音声認識部９０は、信号強調部８０から各目的信号の波形を受け取って、これに既存の音声認識技術を適用することで、各目的信号に対する認識結果を出力する。

［システム構成等］
また、図示した各装置の各構成要素は機能概念的なものであり、必ずしも物理的に図示の如く構成されていることを要しない。すなわち、各装置の分散・統合の具体的形態は図示のものに限られず、その全部または一部を、各種の負荷や使用状況等に応じて、任意の単位で機能的または物理的に分散・統合して構成することができる。さらに、各装置にて行われる各処理機能は、その全部または任意の一部が、ＣＰＵおよび当該ＣＰＵにて解析実行されるプログラムにて実現され、あるいは、ワイヤードロジックによるハードウェアとして実現され得る。

また、本実施形態において説明した各処理のうち、自動的に行われるものとして説明した処理の全部または一部を手動的に行うこともでき、あるいは、手動的に行われるものとして説明した処理の全部または一部を公知の方法で自動的に行うこともできる。この他、上記文書中や図面中で示した処理手順、制御手順、具体的名称、各種のデータやパラメータを含む情報については、特記する場合を除いて任意に変更することができる。

［プログラム］
実施形態の信号処理装置１〜５は、パッケージソフトウェアやオンラインソフトウェアとして上記の音源定位、トラッキング、ダイアリゼーション、音声強調、音声認識を実行する信号処理プログラムを所望のコンピュータにインストールさせることによって実装できる。例えば、上記の信号処理プログラムを情報処理装置に実行させることにより、情報処理装置を信号処理装置１〜５として機能させることができる。ここで言う情報処理装置には、デスクトップ型またはノート型のパーソナルコンピュータが含まれる。また、その他にも、情報処理装置にはスマートフォン、携帯電話機やＰＨＳ（Personal Handyphone System）等の移動体通信端末、さらには、ＰＤＡ（Personal Digital Assistant）等のスレート端末等がその範疇に含まれる。

また、信号処理装置１〜５は、ユーザが使用する端末装置をクライアントとし、当該クライアントに上記の信号処理に関するサービスを提供する信号処理サーバ装置として実装することもできる。例えば、信号処理サーバ装置は、観測信号を入力とし、音源の位置を出力とする音源定位サービスを提供するサーバ装置として実装される。この場合、信号処理サーバ装置は、Ｗｅｂサーバとして実装することとしてもよいし、アウトソーシングによって上記の信号処理に関するサービスを提供するクラウドとして実装することとしてもかまわない。

図８は、プログラムが実行されることにより信号処理装置が実現されるコンピュータの一例を示す図である。コンピュータ１０００は、例えば、メモリ１０１０、ＣＰＵ１０２０を有する。また、コンピュータ１０００は、ハードディスクドライブインタフェース１０３０、ディスクドライブインタフェース１０４０、シリアルポートインタフェース１０５０、ビデオアダプタ１０６０、ネットワークインタフェース１０７０を有する。これらの各部は、バス１０８０によって接続される。

メモリ１０１０は、ＲＯＭ（Read Only Memory）１０１１およびＲＡＭ１０１２を含む。ＲＯＭ１０１１は、例えば、ＢＩＯＳ（Basic Input Output System）等のブートプログラムを記憶する。ハードディスクドライブインタフェース１０３０は、ハードディスクドライブ１０９０に接続される。ディスクドライブインタフェース１０４０は、ディスクドライブ１１００に接続される。例えば磁気ディスクや光ディスク等の着脱可能な記憶媒体が、ディスクドライブ１１００に挿入される。シリアルポートインタフェース１０５０は、例えばマウス１１１０、キーボード１１２０に接続される。ビデオアダプタ１０６０は、例えばディスプレイ１１３０に接続される。

ハードディスクドライブ１０９０は、例えば、ＯＳ１０９１、アプリケーションプログラム１０９２、プログラムモジュール１０９３、プログラムデータ１０９４を記憶する。すなわち、信号処理装置１〜５の各処理を規定するプログラムは、コンピュータにより実行可能なコードが記述されたプログラムモジュール１０９３として実装される。プログラムモジュール１０９３は、例えばハードディスクドライブ１０９０に記憶される。例えば、信号処理装置１〜５における機能構成と同様の処理を実行するためのプログラムモジュール１０９３が、ハードディスクドライブ１０９０に記憶される。なお、ハードディスクドライブ１０９０は、ＳＳＤにより代替されてもよい。

また、上述した実施形態の処理で用いられる設定データは、プログラムデータ１０９４として、例えばメモリ１０１０やハードディスクドライブ１０９０に記憶される。そして、ＣＰＵ１０２０が、メモリ１０１０やハードディスクドライブ１０９０に記憶されたプログラムモジュール１０９３やプログラムデータ１０９４を必要に応じてＲＡＭ１０１２に読み出して実行する。

なお、プログラムモジュール１０９３やプログラムデータ１０９４は、ハードディスクドライブ１０９０に記憶される場合に限らず、例えば着脱可能な記憶媒体に記憶され、ディスクドライブ１１００等を介してＣＰＵ１０２０によって読み出されてもよい。あるいは、プログラムモジュール１０９３およびプログラムデータ１０９４は、ネットワーク（ＬＡＮ（Local Area Network）、ＷＡＮ（Wide Area Network）等）を介して接続された他のコンピュータに記憶されてもよい。そして、プログラムモジュール１０９３およびプログラムデータ１０９４は、他のコンピュータから、ネットワークインタフェース１０７０を介してＣＰＵ１０２０によって読み出されてもよい。

１、２、３、４、５ 信号処理装置
１０ 時間周波数分析部
２０ 特徴ベクトル計算部
３０ パラメータ記憶部
４０ 事前確率分布計算部
５０ 音源位置計算部
５１ トラッキング部
６０ ダイアリゼーション部
７０ マスク推定部
８０ 信号強調部
９０ 音声認識部

Claims (7)

1. 複数の異なる位置で取得された収録音に時間周波数分析を適用し、Ｍ次元ベクトルである観測信号ベクトルを計算する時間周波数分析部と、
   前記時間周波数分析部によって計算された観測信号ベクトルの方向の情報を含んだベクトルである特徴ベクトルを、時間周波数点ごとに計算する特徴ベクトル計算部と、
   音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、前記特徴ベクトルの条件付き確率分布のモデルパラメータを記憶するパラメータ記憶部と、
   前記音源位置を表す状態の事前確率分布を荷重とする、前記パラメータ記憶部に記憶されたモデルパラメータに基づく、前記音源位置を表す状態が既知の条件下での、前記特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、前記特徴ベクトル計算部によって計算された特徴ベクトルに当てはめ、前記事前確率分布を計算する事前確率分布計算部と、
   前記事前確率分布計算部によって計算された事前確率分布に基づいて、前記特徴ベクトルに対応する音源位置を計算する音源位置計算部と、
   を有することを特徴とする信号処理装置。
2. 前記事前確率分布計算部は、前記音源位置を表す状態の時間区間ごとの事前確率分布を荷重とする、前記パラメータ記憶部に記憶されたモデルパラメータに基づく、前記音源位置を表す状態が既知の条件下での、前記特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、前記特徴ベクトル計算部によって計算された特徴ベクトルに当てはめ、前記時間区間ごとの事前確率分布を計算し、
   音源位置計算部は、前記事前確率分布計算部によって計算された前記時間区間ごとの事前確率分布に基づいて、前記特徴ベクトルに対応する前記時間区間ごとの音源位置を計算することを特徴とする請求項１に記載の信号処理装置。
3. 前記パラメータ記憶部は、残響下で取得された学習データを用いて学習されたモデルパラメータであって、音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、前記特徴ベクトルの条件付き確率分布のモデルパラメータを記憶することを特徴とする請求項１または２に記載の信号処理装置。
4. 前記パラメータ記憶部は、前記音源位置を表す状態が背景雑音に対応する状態を取る条件下での、条件付き確率分布のモデルパラメータをさらに記憶することを特徴とする請求項１から３のいずれか１項に記載の信号処理装置。
5. 前記事前確率分布計算部は、勾配法に基づいて前記事前確率分布を計算することを特徴とする請求項１から４のいずれか１項に記載の信号処理装置。
6. 信号処理装置で実行される信号処理方法であって、
   複数の異なる位置で取得された収録音に時間周波数分析を適用し、Ｍ次元ベクトルである観測信号ベクトルを計算する時間周波数分析工程と、
   前記時間周波数分析工程によって計算された観測信号ベクトルの方向の情報を含んだベクトルである特徴ベクトルを、時間周波数点ごとに計算する特徴ベクトル計算工程と、
   音源位置を表す状態が複数の音源位置候補のそれぞれに対応する状態を取る条件下での、前記特徴ベクトルの条件付き確率分布のモデルパラメータを記憶するパラメータ記憶部に記憶されたモデルパラメータを取得し、前記音源位置を表す状態の事前確率分布を荷重とする、前記モデルパラメータに基づく、前記音源位置を表す状態が既知の条件下での、前記特徴ベクトルの条件付き確率分布の荷重和である混合モデルを、前記特徴ベクトル計算工程によって計算された特徴ベクトルに当てはめ、前記事前確率分布を計算する事前確率分布計算工程と、
   前記事前確率分布計算工程によって計算された事前確率分布に基づいて、前記特徴ベクトルに対応する音源位置を計算する音源位置計算工程と、
   を含んだことを特徴とする信号処理方法。
7. コンピュータを、請求項１から５のいずれか１項に記載の信号処理装置として機能させるための信号処理プログラム。

Images