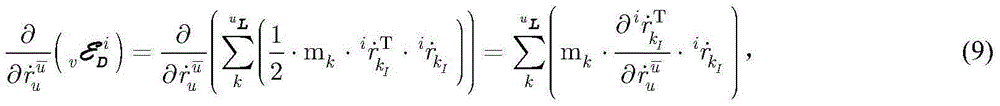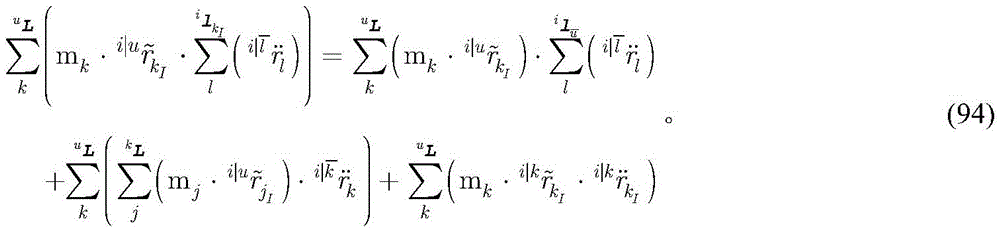CN109117451B - Tree chain robot dynamics modeling and resolving method based on axis invariants - Google Patents
Tree chain robot dynamics modeling and resolving method based on axis invariants Download PDFInfo
- Publication number
- CN109117451B CN109117451B CN201810933332.3A CN201810933332A CN109117451B CN 109117451 B CN109117451 B CN 109117451B CN 201810933332 A CN201810933332 A CN 201810933332A CN 109117451 B CN109117451 B CN 109117451B
- Authority
- CN
- China
- Prior art keywords
- axis
- formula
- equation
- chain
- mass
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Active
Links
- 238000000034 method Methods 0.000 title claims abstract description 81
- 239000011159 matrix material Substances 0.000 claims abstract description 106
- 238000004364 calculation method Methods 0.000 claims abstract description 31
- 230000008569 process Effects 0.000 claims abstract description 26
- 239000013598 vector Substances 0.000 claims description 128
- 238000013519 translation Methods 0.000 claims description 39
- 230000001133 acceleration Effects 0.000 claims description 38
- 230000014509 gene expression Effects 0.000 claims description 16
- 230000005484 gravity Effects 0.000 claims description 14
- 238000000354 decomposition reaction Methods 0.000 claims description 11
- 230000007613 environmental effect Effects 0.000 claims description 9
- 238000002360 preparation method Methods 0.000 claims description 8
- 230000000996 additive effect Effects 0.000 claims description 7
- 230000009977 dual effect Effects 0.000 claims description 7
- 241000764238 Isis Species 0.000 claims description 6
- 239000000654 additive Substances 0.000 claims description 6
- 230000002146 bilateral effect Effects 0.000 claims description 5
- 230000009471 action Effects 0.000 claims description 4
- 238000005381 potential energy Methods 0.000 claims description 4
- 230000000295 complement effect Effects 0.000 claims description 3
- 239000000463 material Substances 0.000 claims description 3
- 230000017105 transposition Effects 0.000 claims description 3
- 238000009795 derivation Methods 0.000 description 12
- 238000005259 measurement Methods 0.000 description 11
- 239000002245 particle Substances 0.000 description 9
- 230000008901 benefit Effects 0.000 description 7
- 230000009466 transformation Effects 0.000 description 6
- 238000005094 computer simulation Methods 0.000 description 3
- 238000006243 chemical reaction Methods 0.000 description 2
- 238000007596 consolidation process Methods 0.000 description 2
- 230000036544 posture Effects 0.000 description 2
- 239000006126 MAS system Substances 0.000 description 1
- 230000009286 beneficial effect Effects 0.000 description 1
- 238000004422 calculation algorithm Methods 0.000 description 1
- 238000004891 communication Methods 0.000 description 1
- 239000000470 constituent Substances 0.000 description 1
- 230000001419 dependent effect Effects 0.000 description 1
- 238000010586 diagram Methods 0.000 description 1
- 238000001914 filtration Methods 0.000 description 1
- 238000012804 iterative process Methods 0.000 description 1
- 238000005511 kinetic theory Methods 0.000 description 1
- 238000013507 mapping Methods 0.000 description 1
- 238000010606 normalization Methods 0.000 description 1
- 230000003287 optical effect Effects 0.000 description 1
- 229940037201 oris Drugs 0.000 description 1
- 238000012805 post-processing Methods 0.000 description 1
- 238000012545 processing Methods 0.000 description 1
- 230000005631 quantum field theories Effects 0.000 description 1
- 238000011160 research Methods 0.000 description 1
- 230000004044 response Effects 0.000 description 1
- 238000004088 simulation Methods 0.000 description 1
- 238000005303 weighing Methods 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/11—Complex mathematical operations for solving equations, e.g. nonlinear equations, general mathematical optimization problems
-
- G—PHYSICS
- G06—COMPUTING; CALCULATING OR COUNTING
- G06F—ELECTRIC DIGITAL DATA PROCESSING
- G06F17/00—Digital computing or data processing equipment or methods, specially adapted for specific functions
- G06F17/10—Complex mathematical operations
- G06F17/16—Matrix or vector computation, e.g. matrix-matrix or matrix-vector multiplication, matrix factorization
Landscapes
- Engineering & Computer Science (AREA)
- Physics & Mathematics (AREA)
- Mathematical Physics (AREA)
- General Physics & Mathematics (AREA)
- Pure & Applied Mathematics (AREA)
- Theoretical Computer Science (AREA)
- Mathematical Analysis (AREA)
- Mathematical Optimization (AREA)
- Computational Mathematics (AREA)
- Data Mining & Analysis (AREA)
- Algebra (AREA)
- Databases & Information Systems (AREA)
- Software Systems (AREA)
- General Engineering & Computer Science (AREA)
- Operations Research (AREA)
- Computing Systems (AREA)
- Manipulator (AREA)
- Feedback Control In General (AREA)
Abstract
The invention discloses a tree chain robot dynamics and resolving method based on axis invariants, and provides and proves a Ju-Kane dynamics model, which is suitable for the dynamics numerical calculation of a tree chain multi-axis system and the dynamics control of the multi-axis system. The system analyzes the characteristics of the generalized inertia matrix of the rigid body of the shaft chain and the generalized inertia matrix of the rigid system of the shaft chain; the principle and the process of multi-axis system dynamics positive solution are given, and when GPU calculation is applied, linear complexity is achieved; when applying single CPU computation, there is a squared complexity. The principle and the process of the multi-axis system dynamics inverse solution are given, and the linear complexity is achieved; due to the small system inertia matrix, the computational complexity of the dynamics of the multi-axis system is much lower than that of the existing known dynamics systems.
Description
Technical Field
The invention relates to a tree chain robot dynamics modeling and resolving method, and belongs to the technical field of robots.
Background
Lagrange provides a Lagrange method in the process of researching the lunar translation problem, and the Lagrange method is a basic method for expressing a kinetic equation by a generalized coordinate; meanwhile, the method is also a basic method for describing the quantum field theory. Establishing a kinetic equation by applying a Lagrange method is a complicated process, and although the Lagrange equation deduces the kinetic equation of a system according to the invariance of system energy, the Lagrange equation has the advantage of theoretical analysis; however, in engineering application, as the degree of freedom of the system increases, the complexity of equation derivation increases dramatically, and the general application is difficult. Compared with the Lagrange equation, the Keynen equation establishing process directly expresses a kinetic equation through the bias speed, the speed and the acceleration of the system. Compared with the Lagrange method, the Keyness dynamics method greatly reduces the difficulty of system modeling due to the fact that the expression of system energy and the derivation process of time are omitted. However, for a system with high degree of freedom, the kahn dynamics modeling method is also difficult to apply.
The Lagrange equation and the Kane equation greatly promote the research of multi-body dynamics, and the calculation speed and the calculation precision of the dynamics based on the space operator algebra are improved to a certain extent due to the application of the iterative process. The dynamics methods need to perform complex transformation in a body space, a body subspace, a system space and a system subspace no matter in a kinematics process or a dynamics process, the modeling process and model expression are very complex, and the requirements of high-freedom system modeling and control are difficult to meet, so that a concise expression of a dynamics model needs to be established; the modeling accuracy and the modeling instantaneity are guaranteed. Without a concise dynamics expression, the reliability and accuracy of the high-freedom system dynamics engineering realization are difficult to guarantee. Meanwhile, the traditional unstructured kinematics and dynamics symbols cannot be understood by a computer by annotating the connotation of the convention symbols, so that the computer cannot autonomously establish and analyze kinematics and dynamics models.
Disclosure of Invention
The invention aims to solve the technical problem of providing a tree chain robot dynamics and resolving method based on axis invariants.
In order to solve the technical problems, the invention adopts the following technical scheme:
a tree chain robot dynamics and resolving method based on axis invariants is characterized by comprising the following steps:
given a multi-axis rigid system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F[i],The resultant force and moment acting on the axis u, in addition to gravity, are respectively recorded asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k of
According to the topological, structural and mass inertia parameters of the robot system, a Lagrange equation of a joint space is established by using a chain symbolic system, and a Ju-Kane dynamics preparation equation is established based on the Lagrange equation of a multi-axis system;
substituting the bias speed into a Ju-Kane dynamics preparatory equation to establish a Ju-Kane dynamics equation of a tree-link rigid system;
establishing a Ju-Kane normalized kinetic equation of a tree structure rigid body system;
and (4) restating a chain rigid system Ju-Kane kinetic equation into a chain Ju-Kane normative equation.
A Lagrange equation derivation Cure-Kane (Ju-Kane) dynamics preparation theorem based on a multi-axis system comprises the following steps:
【1】 The equivalence of a Lagrange equation and a Kane equation is proved;
【2】 Based on Lagrange's equation, based on the energy to the joint velocity and the bias velocity of the coordinate;
【3】 Calculating the derivative of the deflection speed to the time;
【4】 The Ju-Kane kinetic preliminary theorem is obtained based on the above steps.
【1】 Proving the equivalence of the Lagrange equation and the Kane equation
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translational acceleration vector;is a translation velocity vector;is moved in translationEnergy is saved;is rotational kinetic energy;is a joint coordinate;is the joint velocity;
considering rigid k translation kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Considering rigid k rotational kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Due to the fact thatAnduncorrelated, from the Lagrangian equation of equation (7) and multiaxial systems
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is translational kinetic energy;is rotational kinetic energy;is gravitational potential energy;is a joint coordinate;is the joint velocity;
the translation kinetic energy and the rotation kinetic energy of the kinetic system D are respectively expressed as
Considering formula (4) and formula (5), namely, there are
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
equations (7) and (8) are the proof of the Ju-Kane dynamics preparation theorem, that is, the Ju-Kane dynamics preparation theorem is essentially equivalent to the Lagrange method; meanwhile, the right side of the formula (8) comprises a multiaxial system Kane equation; the inertia force calculation of the Lagrange method and the Keynen method is consistent, namely the Lagrange method and the Keynen method are equivalent;
【2】 Based on Lagrange's equation, the deviation speed of joint speed and coordinate based on energy
Wherein:
[ 2-1 ] AAnd take into accountAndonly with closed treeRelated, by formula (4) and formula (5), to obtain
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translation velocity vector;is a joint coordinate;is the joint velocity;
[ 2-2 ] AAnd take into accountAndonly with closed treeRelated, by formula (4) and formula (5), to obtain
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translation velocity vector;is the coordinate of the rotary joint;is the rotational joint speed;
【3】 Derivative of bias speed with respect to time
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
【4】 Ju-Kane dynamics preliminary theorem obtained based on the steps
The preliminary Ju-Kane dynamics equation for axis u is
Equation (17) has a tree chain topology; k is a radical ofIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is a translational joint coordinate;is the translational joint speed;is the coordinate of the rotary joint;is the rotational joint speed; closed treeThe generalized force in (1) has additive property, the node of the closed subtree has only one kinematic chain to the root, and the kinematic chainCan be used as a moving chainAnd (6) replacing.
in the formula, along the axisPosition of the threadAround shaftAngular position ofAxial vectorMeasurement ofAngular velocityLinear velocity
The left-order cross product and transposition relationship is:
Given a point of application i in a free environment iSTo point l on axis lSDouble-sided external force ofAnd external momentTheir instantaneous shaft power pexIs shown as
In the formula (26)And in formula (21)The chain sequences of (A) and (B) are different; the former is acting force, the latter is movement amount, the two are dual and have opposite orders;
The formulae (26) and (27) indicate environmental effectsThe resultant force or moment applied to the axis k being equivalent to a closed treeThe resultant external force or moment on the axis k is expressed by the sum of the expressions (26) and (27)
In equation (28), the closed tree has additive generalized force to axis k; the action of the force has a dual effect and is backward iterative; by reverse iteration is meant:is required to iterate through the link position vector;order and forward kinematics ofThe order of calculation is reversed.
If the shaft is a drive shaft, the drive force and drive torque of the shaft are respectivelyAnddriving forceAnd driving torqueGenerated power pacIs shown as
【1】 From formula (18), formula (19) and formula (29)
If the axis u is parallel to the axisIs coaxial, then hasNote the book Due to the fact thatAndindependently of each other, from the formula (30)
【2】 From formula (18), formula (19) and formula (29)
The resultant external force and moment acting on the shaft uThe components above are respectively noted asAndbilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe force and moment of environment i to axis are respectivelyAndthen the axial u tree chain Ju-Kane kinetic equation is
Wherein: [. the]Representing taking a row or a column;andis a 3 x 3 block matrix,andis a 3D vector, q is joint space;
and is provided with a plurality of groups of the materials,
wherein, noteNote the book kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd an inertia matrix for the rotation axis u;an inertia matrix being a translation axis u; h isRA non-inertial matrix of rotation axis u; h isPA non-inertial matrix of the translational axis u.
Definition of
The Ju-Kane normalized kinetic equation of the tree structure rigid system is as follows:
the canonical form of the formula (36) is
The canonical form of the formula (37) is
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is an axis invariant;is the joint acceleration;as cross-multipliers, vectorsIs cross-multiplication matrix of To take from axis i to axisIs connected with the kinematic chainThe representation obtains a closed subtree consisting of the axis u and its subtree.
And (3) restating a chain rigid system Ju-Kane kinetic equation into a chain Ju-Kane normative equation:
given a multi-axis rigid system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F[i],The resultant force and moment acting on the axis u in addition to gravity isThe components above are respectively noted asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k ofBilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the moment of the environment i to the shaft are respectivelyAndthen the Ju-Kane dynamics specification equation of axis u is
And,
in the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd an inertia matrix for the rotation axis u;an inertia matrix being a translation axis u; h isRA non-inertial matrix of rotation axis u; h isPA non-inertial matrix for the translational axis u; the resultant external force and moment acting on the shaft uThe components above are respectively noted asAnd bilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the acting moment of the environment i on the shaft are respectivelyAnd to take the kinematic chain from axis l to axis k,the representation obtains a closed subtree consisting of the axis u and its subtree.
And (3) given the generalized force of the environmental action and the generalized driving force of the driving shaft, solving the acceleration or inertial acceleration of the dynamic system to obtain the forward solution of the Ju-Kane dynamic equation of the tree-link rigid system.
The specific steps of solving the positive solution of the Ju-Kane kinetic equation of the tree-chain rigid system are as follows:
Arranging the Ju-Kane dynamics standard equations of all axes in the system according to lines; the rearranged shaft driving generalized force and the immeasurable environmental acting force are recorded as fCMeasurable environmental generalized acting force is denoted as fi(ii) a The corresponding joint acceleration sequence is recorded asAfter rearrangementRecording as h; the system dynamics equation is
Is obtained by the formula (125)
The generalized inertia matrix of the system with the number of axes a is recorded as M3a×3a;
Axle chain generalized inertia matrixIs a symmetric matrix and it is a positive definite matrix, effectivelyThe calculation process is as follows:
【1】 First, LDL is applied to the resultantTThe decomposition is a matrix decomposition, i.e.,
Substituting formula (130) for formula (128)
Thus, a positive solution of the Ju-Kane kinetic equation of the tree-chain rigid system is obtained.
Solving the inverse solution of the Ju-Kane kinetic equation of the tree-chain rigid system.
When the joint configuration, velocity and acceleration are known, the joint configuration is obtained by the formula (34)Andwhen the external force and the external moment are known, the driving force is solved by equation (132)And driving torque
Wherein the resultant force and moment acting on the axis u isThe components above are respectively noted asAnd bilateral driving force and driving torque of driving shaft uIn thatThe components above are respectively noted asAndthe acting force and the acting moment of the environment i on the shaft are respectivelyAnd to take the kinematic chain from axis l to axis k,the representation obtains a closed subtree consisting of the axis u and its subtree.
The invention achieves the following beneficial effects:
the invention provides and proves a Ju-Kane dynamics model, which is suitable for the dynamics numerical calculation of a tree chain multi-axis system and the dynamics control of the multi-axis system. The system analyzes the characteristics of the generalized inertia matrix of the rigid body of the shaft chain and the generalized inertia matrix of the rigid system of the shaft chain; the principle and the process of multi-axis system dynamics positive solution are given, and when GPU calculation is applied, linear complexity is achieved; when applying single CPU computation, there is a squared complexity. The principle and the process of the multi-axis system dynamics inverse solution are given, and the linear complexity is achieved; due to the small system inertia matrix, the computational complexity of the dynamics of the multi-axis system is much lower than that of the existing known dynamics systems. Is characterized in that:
【1】 The 3D generalized inertia matrix space shown in equation (114) is more compact, being 1/4 of 6D inertia matrix size;
【2】 An explicit expression of a generalized inertia matrix of the system can be directly written through an iterative equation;
【3】 The forward and inverse dynamics calculation has linear complexity;
【4】 Meanwhile, the method has the basic characteristics of the Ju-Kane standard equation.
Drawings
FIG. 1 a natural coordinate system and axis chain;
FIG. 2 is a fixed axis invariant;
fig. 3 is a 3R robot arm.
Detailed Description
The invention is further described below. The following examples are only for illustrating the technical solutions of the present invention more clearly, and the protection scope of the present invention is not limited thereby.
Define 1 natural coordinate axes: a unit reference axis having a fixed origin, referred to as being coaxial with the axis of motion or measurement, is a natural coordinate axis, also referred to as the natural reference axis.
Defining 2 a natural coordinate system: as shown in fig. 1, if the multi-axis system D is located at the zero position, the directions of all cartesian body coordinate systems are the same, and the origin of the body coordinate system is located on the axis of the moving shaft, the coordinate system is a natural coordinate system, which is simply referred to as a natural coordinate system.
The natural coordinate system has the advantages that: (1) the coordinate system is easy to determine; (2) the joint variable at zero is zero; (3) the system postures at the zero position are consistent; (4) and accumulated errors of measurement are not easily introduced.
From definition 2, it can be seen that the natural coordinate system of all the rods coincides with the orientation of the base or world system when the system is in the zero position. With the system in zero positionTime, natural coordinate systemVector around axisAngle of rotationWill be provided withGo to F[l];In thatCoordinate vector ofAt F[l]Coordinate vector ofIs constant, i.e. has
According to the formula, the method has the advantages that,orIndependent of adjacent coordinate systemsAndso it is calledOrIs axis invariant. When invariance is not emphasized, the method can be called a coordinate axis vector (axis vector for short).OrCharacterized by being a bodyCoordinate vector of reference unit common to body l, and reference pointAnd OlIs irrelevant. BodyThe body l is a rod or a shaft.
The axis invariants are essentially different from coordinate axes:
(1) the coordinate axis is a reference direction with a zero position and unit scales, and can describe the position of translation along the direction, but cannot completely describe the rotation angle around the direction, because the coordinate axis does not have a radial reference direction, namely, the zero position representing rotation does not exist. In practical applications, the radial reference of the shaft needs to be supplemented. For example: in the Cartesian system F[l]In the rotation around lx, ly or lz is used as a reference zero position. The coordinate axes themselves are 1D, with 3 orthogonal 1D reference axes constituting a 3D cartesian frame.
(2) The axis invariant is a 3D spatial unit reference axis, which is itself a frame. It itself has a radial reference axis, i.e. a reference null. The spatial coordinate axes and their own radial reference axes may define cartesian frames. The spatial coordinate axis may reflect three basic reference properties of the motion axis and the measurement axis.
The axis vector of the chainless index is recorded in the literatureAnd is called the Euler Axis (Euler Axis), and the corresponding joint Angle is called the Euler Angle. The present application is no longer followed by the euler axis, but rather is referred to as the axis invariant because the axis invariant has the following properties:
【1】 Given rotation transformation arraySince it is a real matrix whose modes are unity, it has a real eigenvalue λ1And two complex eigenvalues conjugated to each otherAndwherein: i is a pure imaginary number. Therefore, | λ1|·||λ2||·||λ 31, to obtain lambda 11. Axial vectorIs a real eigenvalue λ 11, is an invariant;
【2】 Is a 3D reference shaft, not only having an axial reference direction, but also having a radial reference null, as will be described in section 3.3.1.
【3】 Under a natural coordinate system:i.e. axial invariantIs a very special vector, has invariance to the derivative of time and has very good mathematical operation performance;
for an axis invariant, its absolute derivative is its relative derivative. Since the axis invariant is a natural reference axis with invariance, its absolute derivative is always a zero vector. Thus, the axis invariants have invariance to the time differential. Comprises the following steps:
【4】 In a natural coordinate system, passing an axial vectorAnd joint variablesCan directly describe the rotating coordinate arrayIt is not necessary to establish a separate system for the rods other than the roots. Meanwhile, the measurement precision of the system structure parameters can be improved by taking the only root coordinate system to be defined as reference;
【5】 Using axial vectorsThe method has the advantages that a completely parameterized unified multi-axis system kinematics and dynamics model comprising a topological structure, a coordinate system, a polarity, a structure parameter and a mechanics parameter is established.
Factor vector elIs a reaction of with F[l]Any vector, base vector, of consolidationIs andany vector of consolidation, in turnIs F[l]Anda common unit vector, thereforeIs thatAnda common basis vector. Thus, the axis is invariantIs F[l]Andcommon reference base. The axis invariants are parameterized natural coordinate bases, and are primitives of the multi-axis system. The translation and rotation of the fixed shaft invariant are equivalent to the translation and rotation of a coordinate system fixedly connected with the fixed shaft invariant.
When the system is in a zero position, the natural coordinate system is used as a reference, and coordinate axis vectors are obtained through measurementIn the kinematic pairAxial vector during motionIs an invariant; axial vectorAnd joint variablesUniquely identifying kinematic pairThe rotational relationship of (1).
Thus, with the natural coordinate system, only a common reference frame need be determined when the system is in the null position, rather than having to determine individual body coordinate systems for each rod in the system, as they are uniquely determined by the axis invariants and the natural coordinates. When performing system analysis, the other natural coordinate systems, apart from the base system, to which the bars are fixed, only occur conceptually, and are not relevant to the actual measurement. The theoretical analysis and engineering functions of a natural coordinate system on a multi-axis system (MAS) are as follows:
(1) the measurement of the structural parameters of the system needs to be measured by a uniform reference system; otherwise, not only is the engineering measurement process cumbersome, but the introduction of different systems introduces greater measurement errors.
(2) A natural coordinate system is applied, and except for the root rod piece, the natural coordinate systems of other rod pieces are naturally determined by the structural parameters and the joint variables, so that the kinematics and dynamics analysis of the MAS system is facilitated.
(3) In engineering, the method can be applied to optical measurement equipment such as a laser tracker and the like to realize the accurate measurement of the invariable of the fixed shaft.
(4) As the kinematic pairs R and P, the spiral pair H and the contact pair O are special cases of the cylindrical pair C, the MAS kinematics and dynamics analysis can be simplified by applying the cylindrical pair.
Define 4 rotational coordinate vectors: vector around coordinate axisRotated to an angular positionCoordinate vector ofIs composed of
Define 5 translation coordinate vectors: vector along coordinate axisTranslation to linear positionCoordinate vector ofIs composed of
Define 6 natural coordinates: taking the vector of the natural coordinate axis as a reference direction, and marking the angular position or linear position of the zero position of the relative system as ql, which is called as a natural coordinate; weighing the quantity mapped one by one with the natural coordinate as a joint variable; wherein:
define 7 mechanical zero: for kinematic pairAt an initial time t0Zero position of time, joint absolute encoderNot necessarily zero, which is called mechanical zero;
Defining 8 natural motion vectors: will be represented by natural coordinate axis vectorsAnd natural coordinate qlDetermined vectorReferred to as natural motion vectors. Wherein:
the natural motion vector realizes the shaft translation andunified representation of rotation. Vectors to be determined from natural coordinate axis vectors and joints, e.g.Called free motion vector, also called free helix. Obviously, axial vectorIs a specific free helix.
Define 9 the joint space: by joint natural coordinates qlThe space represented is called joint space.
Define a 10-bit shape space: a cartesian space expressing a position and a posture (pose for short) is called a configuration space, and is a dual vector space or a 6D space.
Defining 11 a natural joint space: with reference to natural coordinate system and by joint variablesIndicating that there must be at system zeroIs called the natural joint space.
As shown in FIG. 2, a given linkOrigin OlPosition-dependent vectorConstrained axis vectorIs a fixed axis vector, is denoted asWherein:
axial vectorIs the natural reference axis for the natural coordinates of the joint. Due to the fact thatIs an axis invariant, so it is calledFor the invariants of fixed axes, it characterizes kinematic pairsThe natural coordinate axis is determined. Fixed shaft invariantIs a chain linkNatural description of structural parameters.
Defining 12 a natural coordinate axis space: the fixed axis invariant is used as a natural reference axis, and a space represented by corresponding natural coordinates is called a natural coordinate axis space, which is called a natural axis space for short. It is a 3D space with 1 degree of freedom.
As shown in figure 2 of the drawings, in which,andwithout rod omegalIs a constant structural reference.Determines the axis l relative to the axisFive structural parameters of (a); and joint variable qlTogether, the rod omega is expressed completelylThe 6D bit shape. Given aThe natural coordinate system of the fixed rod can be determined by the structural parametersAnd joint variablesAnd (4) uniquely determining. Balance shaft invariantFixed shaft invariantVariation of jointAndis naturally invariant. Obviously, invariant by a fixed axisAnd joint variablesNatural invariance of constituent jointsAnd from a coordinate systemTo F[l]Determined spatial configurationHaving a one-to-one mapping relationship, i.e.
Given a multi-axis system D ═ T, a, B, K, F, NT }, in the system null position, only the base or inertial frame is established, as well as the reference points O on the axeslOther rod coordinate systems are naturally determined. Essentially, only the base or inertial frame need be determined.
Given a structural diagram with a closed chain connected by kinematic pairs, any kinematic pair in a loop can be selected, and a stator and a mover which form the kinematic pair are divided; thus, a loop-free tree structure, called Span tree, is obtained. T represents a span tree with direction to describe the topological relation of tree chain motion.
I is a structural parameter; a is an axis sequence, F is a rod reference system sequence, B is a rod body sequence, K is a kinematic pair type sequence, and NT is a sequence of constraint axes, i.e., a non-tree.For taking an axis sequenceIs a member of (1). The revolute pair R, the prismatic pair P, the helical pair H and the contact pair O are special cases of the cylindrical pair C.
The basic topological symbol and operation for describing the kinematic chain are the basis for forming a kinematic chain topological symbol system, and are defined as follows:
【1】 The kinematic chain is identified by a partially ordered set (].
【2】A[l]Is a member of the axis-taking sequence A; since the axis name l has a unique number corresponding to A[l]Number of (2), therefore A[l]The computational complexity is O (1).
【3】Is a father axis of the taking axis l; shaftThe computational complexity of (2) is O (1). The computation complexity O () represents the number of operations of the computation process, typically referred to as the number of floating point multiplies and adds. To floatThe point multiplication and addition times express the complexity of calculation, so the main operation times in the algorithm circulation process are often adopted; such as: joint pose, velocity, acceleration, etc.
【5】To take the kinematic chain from axis l to axis k, the output is represented asAnd isBase number is noted as The execution process comprises the following steps: executeIf it isThen executeOtherwise, ending.The computational complexity is
【6】Are children of the axis l. The operation is represented inFinding the address k of the member l; thus, a sub-A of the axis l is obtained[k]. Due to the fact thatHas no off-order structure, thereforelThe computational complexity of l is
【7】Representing the acquisition of a closed subtree made up of the axis l and its subtrees,is a subtree without l; recursive executionThe computational complexity is
【8】 Adding and deleting operations of branches, subtrees and non-tree arcs are also necessary components; thus, the variable topology is described by a dynamic Span tree and a dynamic graph. In the branchIn, ifThen rememberNamely, it isRepresenting the child of member m taken in the branch.
The following expression or expression form is defined:
the shafts and the rod pieces have one-to-one correspondence; quantity of property between axesAnd the amount of attribute between the rodsHas the property of order bias.
Appointing: "□" represents an attribute placeholder; if the attribute P or P is location-related, thenIs understood to be a coordinate systemTo F[l]The origin of (a); if the property P or P is directional, thenIs understood to be a coordinate systemTo F[l]。
Andare to be understood as a function of time t, respectivelyAndand isAndis t0A constant or array of constants at a time. But in the bodyAndshould be considered a constant or an array of constants.
In the present application, the convention: in a kinematic chain symbolic operation system, attribute variables or constants with partial order include indexes representing partial order in name; or the upper left corner and the lower right corner, or the upper right corner and the lower right corner; the direction of the parameters is always from the upper left corner index to the lower right corner index of the partial order index or from the upper right corner index to the lower right corner index. For example:can be briefly described as (representing k to l) translation vectors;represents the line position (from k to l);represents a translation vector (from k to l); wherein: r represents the "translation" attribute, and the remaining attributes correspond to: the attribute token phi represents "rotate"; the attribute symbol Q represents a "rotation transformation matrix"; the attribute symbol l represents "kinematic chain"; attribute symbolu represents a "unit vector"; the attribute symbol ω represents "angular velocity"; the angle index i represents an inertial coordinate system or a geodetic coordinate system; other corner marks can be other letters and can also be numbers.
The symbolic specification and convention of the application are determined according to the principle that the sequence bias of the kinematic chain and the chain link are the basic unit of the kinematic chain, and reflect the essential characteristics of the kinematic chain. The chain index represents the connection relation, and the upper right index represents the reference system. The expression of the symbol is simple and accurate, and is convenient for communication and written expression. Meanwhile, the data are structured symbolic systems, which contain elements and relations for forming each attribute quantity, thereby facilitating computer processing and laying a foundation for automatic modeling of a computer. The meaning of the index needs to be understood through the context of the attribute symbol; such as: if the attribute symbol is of a translation type, the index at the upper left corner represents the origin and the direction of a coordinate system; if the attribute is of the pivot type, the top left indicator represents the direction of the coordinate system.
(1)lS-a point S in the bar l; and S denotes a point S in space.
andare respectively atAnd F[l]A lower coordinate vector;is an axis invariant, being a structural constant;
as rotation vector, rotation vector/angle vectorIs a free vector, i.e., the vector is free to translate;
(7) when the index of the lower left corner is 0, the index represents a mechanical zero position; such as:
(8) 0-three-dimensional zero matrix; 1-a three-dimensional identity matrix;
Power symbolTo representTo the x-th power of; the right upper corner is marked with ^ orA representation separator; such as:orIs composed ofTo the x power of.
To representThe transpose of (1) indicates transposing the set, and no transpose is performed on the members; such as:
the projection symbol is a projection vector or a projection sequence of a vector or a second-order tensor to a reference base, namely a coordinate vector or a coordinate array, and the projection is dot product operation "·"; such as: position vectorIn a coordinate system F[k]The projection vector in (1) is recorded as
Is a cross multiplier; such as:is axis invariantA cross-product matrix of; given any vectorIs cross-multiplication matrix ofThe cross-multiplication matrix is a second order tensor.
Cross-multiplier operations have a higher priority than projectersThe priority of (2). Projecting signIs higher priority than the member access characterOrMember access signPriority higher than power symbol
(11)Zero position by origin OlTo the origin OlIs translated by the vector ofRepresenting the location structure parameter.
(13) taking the vector of the natural coordinate axis as a reference direction, and marking the angular position or linear position of the zero position of the system as qlCalled natural coordinates; variation of jointNatural joint coordinate phil;
(14) For a given ordered set r ═ 1,4,3,2]TRemember r[x]The representation takes the x-th row element of the set r. Frequently remembered [ x ]]、[y]、[z]And [ omega ]]This is shown with the elements in columns 1, 2, 3 and 4.
given kinematic chainIf n represents a Cartesian rectangular system, it is calledIs a Cartesian axis chain; if n represents a natural reference axis, then callIs a natural axis chain.
1. Lagrange equation for establishing multi-axis system
A Lagrange equation of a joint space is established by applying a chain symbol system, a particle dynamics system D is considered to be { A, K, T, NT, F and B }, and free particles are deduced according to Newton mechanicsLagrange's equation of (a); then generalize to constrained particle systems.
Conservative forceRelative mass point inertia forceHaving the same strand order, i.e.Has positive sequence and particleThe resultant force of the two is zero. ParticleEnergy of is recorded asAccording to a generalized coordinate sequenceWith a cartesian spatial position vector sequenceRelationships between
To obtain
And (3) applying the energy and the generalized coordinate of the system to establish an equation of the system. Variation of jointAnd coordinate vectorThe relationship of (a) is shown in formula (1), and the formula (1) is called as point transformation of joint space and Cartesian space.
Conservative forces have an opposite chain order to inertial forces. The constraint in the Lagrange system can be fixed constraint between particle points and motion constraint between particle point systems; rigid body is itself a particle systemThe particle energy is additive; the rigid body kinetic energy consists of mass center translational kinetic energy and rotational kinetic energy. And then, establishing Lagrange equations respectively by using the simple kinematic pairs R/P, and laying a foundation for further deducing a new kinetic theory subsequently.
Given a rigid-body multi-axis system D ═ { a, K, T, NT, F, B }, the inertial space is denoted as i,the energy of the axis l is recordedWherein the translational kinetic energy isKinetic energy of rotation ofGravitational potential energy isThe shaft is subjected to external resultant force and resultant moment except the gravitational force respectivelyAndthe mass of the shaft l and the mass center moment of inertia are mlAndthe unit axis invariance of the axis u isThe environment i acts onIIs recorded as the inertial accelerationAcceleration of gravityThe chain sequence is from i to lI;The chain sequence is composed ofITo i; and is provided with
【1】 Energy of system
Wherein:
【2】 Lagrange equation for multiaxial systems
From the multi-axis system lagrange equation of equation (2),
equation (6) is a governing equation for the axis u, i.e. invariant on the axisThe force balance equation above;is a resultant forceIn thatThe component of (a) to (b),is resultant momentIn thatThe component (c) above.
2. Establishing a Ju-Kane dynamics preparatory equation:
and (4) deriving a Jue-Kane (Ju-Kane) dynamics preliminary theorem based on the Lagrange equation (6) of the multi-axis system. Firstly, carrying out equivalence proof of a Lagrange equation and a Kane equation; then, calculating the deviation speed of the energy to the joint speed and the coordinate, then obtaining the time derivation, and finally giving out the Ju-Kane dynamics preparation theorem.
【1】 Proof of equivalence of Lagrange equation and Kane equation
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translational acceleration vector;is a translation velocity vector;is translational kinetic energy;is rotational kinetic energy;is a joint coordinate;is the joint velocity;
the specific establishment steps of the above formula are as follows: considering rigid k translation kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Considering rigid k rotational kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Due to the fact thatAnduncorrelated, from equation (7) and the Lagrangian equation (6) for multiaxial systems
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is translational kinetic energy;is rotational kinetic energy;is gravitational potential energy;is a joint coordinate;is the joint velocity;
the translation kinetic energy and the rotation kinetic energy of the kinetic system D are respectively expressed as
Considering formula (4) and formula (5), namely, there are
Equations (7) and (8) are the basis for the proof of the Jurkinj dynamics preparatory theorem, i.e., the Jurkinj dynamics preparatory theorem is essentially equivalent to the Lagrange method. Meanwhile, the right side of the formula (8) comprises a multiaxial system Kane equation; the inertia force calculation of the Lagrange method is consistent with that of the Keynen method, namely the Lagrange method and the Keynen method are equivalent. Formula (8) indicates that: in Lagrange's equation (4)The problem of duplicate calculations.
【2】 Energy vs. joint velocity and coordinate yaw rate
[ 2-1 ] AAnd take into accountAndonly with closed treeRelated, by formula (4) and formula (5), to obtain
[ 2-2 ] AAnd take into account Andonly with closed treeRelated, by formula (4) and formula (5), to obtain
At this point, the energy vs. joint velocity and coordinate yaw rate calculations have been completed.
【3】 Derivation of time
By this, the derivation of the time t has been completed.
【4】 Ju-Kane kinetics preliminary theorem
Substituting the formula (11), the formula (14), the formula (15) and the formula (16) into the formula (8),
given a multi-axis rigid body system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F [ i ═ i],The resultant force and moment acting on the axis u, in addition to gravity, are respectively recorded asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k ofThen the preliminary Ju-Kane dynamics equation for axis u is
Equation (17) has a tree chain topology. k is a radical ofIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is a translational joint coordinate;is the translational joint speed;is the coordinate of the rotary joint;is the rotational joint speed; the nodes of the closed subtree thus have only one kinematic chain to the root, and the kinematic chain is thereforeCan be movedAnd (6) replacing.
Next, the right side of equation (17) is solved for the Ju-Kane kinetic preparatory equationAndand (4) calculating to establish a Ju-Kane kinetic equation of the tree-chain rigid system.
3. Building Ju-Kane dynamic model of tree-chain rigid system
the left-order cross product and transposition relationship is:
according to the kinematic iteration formula, there are:
3.1 reverse iteration of external force
Given a point of application i in a free environment iSTo point l on axis lSDouble-sided external force ofAnd external momentTheir instantaneous shaft power pexIs shown as
Namely, it is
In the formula (26)And in formula (21)The chain sequences of (A) and (B) are different; the former is the force and the latter is the amount of exercise, both are dual, with opposite order.
Namely have
The expressions (26) and (27) show that the resultant force or moment of the environment acting on the axis k is equivalent to the closing forceSub treeThe resultant external force or moment on the axis k is expressed by the sum of the expressions (26) and (27)
Therefore, the calculation problem of external force reverse iteration is solved. In equation (28), the closed tree has additive generalized force to axis k; the action of the force has a dual effect and is backward iterative. By reverse iteration is meant:is required to iterate through the link position vector;order and forward kinematics ofThe order of calculation is reversed.
3.2 coaxial drive force reverse iteration
If the shaft is a drive shaft, the drive force and drive torque of the shaft are respectivelyAnddriving forceAnd driving torqueGenerated power pacIs shown as
【1】 From formula (18), formula (19) and formula (29)
Namely, it is
If the axis u is parallel to the axisIs coaxial, then hasNote the book Due to the fact thatAndindependently of each other, from the formula (30)
【2】 From formula (19), formula (18) and formula (29)
Namely, it is
By this, the problem of the coaxial driving force reverse iterative calculation is completed.
3.3 building of the Ju-Kane dynamics explicit model of the tree-chain rigid system:
firstly, a Ju-Kane dynamic equation of a tree chain rigid system is stated, and is called as the Ju-Kane equation for short; then, a setup step is given.
Given a multi-axis rigid system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F[i],The resultant force and moment acting on the axis u in addition to gravity isThe components above are respectively noted asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k ofBilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe force and moment of environment i to axis are respectivelyAndthen the axial u tree chain Ju-Kane kinetic equation is
Wherein: [. the]Representing taking a row or a column;andis a 3 x 3 block matrix,andis a 3D vector and q is the joint space. And is provided with a plurality of groups of the materials,
The establishment steps of the above equation are:
ex has an energy ofpexIs the instantaneous shaft power; p is a radical ofacThe power generated for the driving force and the driving torque of the drive shaft.
Formula (40) is obtained from formula (26), formula (27), formula (31), formula (33) and formula (41).
Substituting the formula (19), the formula (18) and the formula (20) into the Ju-Kane dynamics preparatory equation (17) to obtain the deviation velocity
Is obtained by the formula (21)
Considering equation (43), then
Also, considering the formula (43), the
Substituting formulae (43) to (45) for formula (42) results in formulae (34) to (39).
Example 1
Given a general 3R mechanical arm as shown in FIG. 3, A is (i,1: 3), and the method is applied to establish a tree chain Ju-Kane kinetic equation and obtain a generalized inertia matrix.
Rotation transformation matrix based on axis invariants by equation (46)
To obtain
Kinematic iterative equation:
second order tensor projection:
is obtained from formula (48) and formula (47)
From formula (49), formula (47) and formula (55)
Is obtained from formula (50) and formula (55)
Is obtained from formula (51), formula (55) and formula (57)
Is obtained from formula (52) and formula (55)
Is obtained from formula (53) and formula (55)
And step 2, establishing a kinetic equation. The equation of the dynamics of the 1 st axis is established. Is obtained by the formula (37)
Is obtained by the formula (39)
The equation of the dynamics of the 1 st axis is obtained from the equations (61) and (62),
and establishing a kinetic equation of the 2 nd axis. Is obtained by the formula (37)
Is obtained by the formula (39)
The equation of dynamics of the 2 nd axis is obtained from the equations (64) and (65),
finally, the 3 rd axis dynamical equation is established. Is obtained by the formula (37)
Is obtained by the formula (39)
The equation of the dynamics of the 3 rd axis is obtained by the equations (67) and (68),
a generalized mass matrix is obtained from the formula (61), the formula (63) and the formula (67).
Therefore, it can be seen that the dynamic modeling can be completed by only formally substituting the parameters of the system, such as topology, structural parameters, mass inertia, etc., into equations (36) to (40). Through programming, the Ju-Kane kinetic equation is easily realized. Because the subsequent tree chain Ju-Kane standard equation is deduced by the Ju-Kane kinetic equation, the effectiveness of the tree chain Ju-Kane kinetic equation can be proved by the Ju-Kane standard example.
3.4 Ju-Kane dynamics normative form of tree chain rigid system
After the system dynamics equations are established, the problem of equation solution is followed. When a dynamic system is simulated, the generalized force of an environmental action and the generalized driving force of a driving shaft are generally given, and the acceleration of the dynamic system needs to be solved; this is a positive problem for the solution of the kinetic equations. Before solving, a specification equation shown in formula (71) needs to be obtained.
The equation of the dynamics is normalized and the dynamic equation is obtained,
wherein: RHS-Right hand side (Right hand side)
Obviously, the normalization process is a process of combining all the joint acceleration terms; thereby, a coefficient of the joint acceleration is obtained. The problem is decomposed into two subproblems of the canonical form of the kinematic chain and the canonical form of the closed tree.
3.4.1 normative equation of the kinematic chain
Converting the forward iteration process of the joint acceleration terms in the formula (36) and the formula (37) into a reverse summation process for subsequent application; obviously, there are 6 different types of acceleration terms, which are processed separately.
The derivation steps of the above formula are:
The derivation steps of the above formula are: consider thatSubstituting formula (72) for formula (75) to the left
The derivation steps of the above formula are: consider thatSubstituting formula (72) for formula (76) to the left
The derivation steps of the above formula are: due to the fact thatTherefore it has the advantages of
3.4.2 normalized equation of closed subtree
Closed treeThe generalized force of (1) is additive; thus, the nodes of the closed subtree have only one kinematic chain to the root, the kinematic chains of equations (73) to (77)Can be covered withAnd (6) replacing. Is obtained by the formula (73)
Is obtained by the formula (74)
Is obtained by the formula (75)
Is obtained by formula (76)
Is obtained by formula (77)
Thus far, the precondition for establishing the standard type is provided.
3.5 Ju-Kane dynamics normative equation of tree-chain rigid system
Next, the Ju-Kane normalized kinetic equation of the tree structure rigid body system is established. For convenience of expression, first define
Then, the formulae (78) to (82) are applied to express the formulae (36) and (37) as normals.
【1】 The canonical form of the formula (36) is
The specific establishment steps of the above formula are as follows: is obtained from the formula (24) and the formula (36)
Is obtained from the formula (52) and the formula (85)
Substituting formula (80) for the right side of formula (85)
Substituting formula (79) for the latter term on the right side of formula (86)
By substituting formula (87) and formula (88) for formula (86)
For rigid body k, there areFormula (84) is obtained from formula (35), formula (83) and formula (89). 【2】 The canonical form of the formula (37) is
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is an axis invariant;is the joint acceleration;as cross-multipliers, vectorsIs cross-multiplication matrix of To take from axis i to axisIs connected with the kinematic chainThe representation obtains a closed subtree consisting of the axis u and its subtree.
The specific establishment steps of the above formula are as follows: is obtained by the formula (37)
Substituting the formula (78) into the right preceding term (91) of the formula
Substituting the formula (81) for the latter term on the right side of the formula (91)
Substituting the formula (82) into the middle of the right side of the formula (91)
Substituting the formula (92), the formula (93) and the formula (94) into the formula (92)
For rigid body k, there areFormula (90) is obtained from formula (35), formula (83) and formula (95).
【3】 Applying the formula (84) and the formula (90), the Ju-Kane equation is restated as the following tree chain Ju-Kane canonical equation:
given multipleThe rigid-axis system D is { a, K, T, NT, F, B }, and the inertia system is denoted as F[i],The resultant force and moment acting on the axis u in addition to gravity isThe components above are respectively noted asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k ofBilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the moment of the environment i to the shaft are respectivelyAndthen the Ju-Kane dynamics specification equation of axis u is
in the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd an inertia matrix for the rotation axis u;an inertia matrix being a translation axis u; h isRA non-inertial matrix of rotation axis u; h isPA non-inertial matrix for the translational axis u; the resultant external force and moment acting on the shaft uThe components above are respectively noted asAnd bilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the acting moment of the environment i on the shaft are respectivelyAnd to take the kinematic chain from axis l to axis k,the representation obtains a closed subtree consisting of the axis u and its subtree.
If the multi-axis rigid body system D includes only the rotation axis,equation (101) can be simplified to
4. Tree chain rigid body Ju-Kane dynamics standard equation solving method
4.1 rigid-body inertia matrix of axle chain
The rigid motion chain generalized inertia matrix expressed according to the motion axis type and the 3D natural coordinate system is called a shaft chain rigid inertia matrix, and is called the shaft chain rigid inertia matrix for short. Is obtained by the formula (116) and the formula (119)
As can be seen from equations (104) and (105), the axis chain inertia matrix is a 3 × 3 matrix, and the size thereof is 4 times smaller than that of the conventional 6 × 6 generalized inertia matrix; accordingly, the inversion complexity is also 4 times less than the conventional inertia matrix.
Order to
And is provided with
Thus, M[u][k]Can be described as
Wherein (114) M[u][k]Is a 3 × 3 axial chain inertia matrix (AGIM), called δkIs a motion axis attribute symbol;
4.2 axle chain rigid body generalized inertia matrix characteristics
Given a multi-axis rigid system D ═ a, K, T, NT, F, B },the rigid inertia matrix of the system axis chain has symmetry under the condition that all kinematic pair types are the same, namely
The derivation steps of the above formula are: setting u to be more than or equal to l. If it isIs represented by the formula (98)
The generalized inertia matrix of the system with the number of axes a is recorded as M3a×3a. Is obtained by formula (115)
Rigid inertial matrix M of axle chain in formula (122)3a×3aHas symmetry, and the element of the axial chain inertia matrix is a 3 multiplied by 3 matrix;
given a multi-axis rigid system D ═ a, K, T, NT, F, B },the shaft chain rigid body inertia matrix element has the following characteristics:
from the above, the elements of the axis chain inertia matrix do not necessarily have symmetry.
Given kinematic chainCartesian coordinate axis sequences are notedWherein:in the form of a sequence of axes of rotation,is a translational axial sequence and has The natural coordinate sequence isIs represented by the formula (98)
Obviously, the rigid body coordinate axis inertia matrix is different from, but equivalent to, the 6D inertia matrix.
4.3 Positive solution of Ju-Kane kinetic equation of tree-chain rigid system
Now, the method for obtaining the forward solution of the Ju-Kane kinetic equation of the tree-chain rigid system is discussed. A positive solution of the kinetic equation refers to solving for joint acceleration or inertial acceleration from the kinetic equation given the driving force.
Given a multi-axis rigid system D ═ a, K, T, NT, F, B },arranging the dynamic equations (96) of all axes in the system according to rows; the rearranged shaft driving generalized force and the immeasurable environmental acting force are recorded as fCMeasurable environmental generalized acting force is denoted as fi(ii) a The corresponding joint acceleration sequence of the system is recorded asAfter rearrangementRecording as h; consider equation (124); the system dynamics equation is
Is obtained by the formula (125)
Wherein,
is obtained by the formula (125)
The generalized inertia matrix of the system with the number of axes a is recorded as M3a×3a. The key is how to compute the inverse of the axis-chain generalized inertia matrix in (128), i.e. theIf a pivoting method is applied for brute force calculationObviously, even for a multi-axis system where the number of axes is not so many, the computational cost is significant. Therefore, this method is not suitable for use.
Axle chain generalized inertia matrixIs a symmetric matrix and is due to system energyGreater than zero, it is a positive definite matrix. Is effectiveThe calculation process is as follows:
【1】 First, LDL is applied to the resultantTThe decomposition is carried out, and the decomposition is carried out,
[ 1-1 ] if LDL is calculated by a single CPUTDecomposition (i.e., matrix decomposition), the decomposition complexity is O (a)2)
Substituting formula (130) for formula (128)
Thus, a positive solution of the Ju-Kane kinetic equation of the tree-chain rigid system is obtained. It has the following characteristics:
[ 2-1 ] axial chain generalized inertia matrix in formula (129) based on Ju-Kane normative formGeneralized inertial matrix with size of only 6D dual-vector spaceAt least one of (a) 1/4 (b),LDL of (2)TThe decomposition greatly improves the inversion speed. Meanwhile, in the formula (131), fC、fiAnd h are all iterative formulas with invariable quantity about the axis, which can ensureSolving forReal-time and accuracy of the system; the Ju-Kane standard type has a rationalization theoretical basis, and the physical content is clear; the multi-body system dynamics based on the 6D space operator is based on the integral incidence matrix, and compared with a Ju-Kane standard system modeling and solving process, the modeling process and the forward solving process are abstract. Particularly, a dynamics iteration method established by using Kalman filtering and a smooth theory is used for reference, and a strict rationalization analysis process is lacked.
Axial chain generalized inertia matrix in equation (129) (2-2)In the formula (131) < f >C、fiAnd h can be dynamically updated according to the system structure, so that the flexibility of engineering application can be ensured.
[ 2-3 ] formula (129) axis chain generalized inertia matrixAnd f in formula (131)C、fiH has a simple and elegant chain index system; meanwhile, the method has a pseudo code function realized by software, and can ensure the quality of engineering realization.
[ 2-4 ] because the polarity of the coordinate system and the axes can be set according to the engineering requirements, the output result of the dynamics simulation analysis does not need to be subjected to intermediate conversion, and the application convenience and the post-processing efficiency are improved.
4.4 inverse solution of Ju-Kane kinetic equation of tree-chain rigid system
The inverse solution of the kinetic equation refers to the solution of the driving force or the driving moment by knowing the kinetic motion state, the structural parameters and the mass inertia. Considering the formula (96) and the formula (102)
When the joint configuration, velocity and acceleration are known, the joint configuration is obtained by the formula (34)Andfurther, if the external force and the external moment are known, the driving force is obtained by the equation (132)And driving torqueObviously, the computational complexity of the inverse solution of the kinetic equation is proportional to the system axis number | a |.
Although the dynamic inverse solution is simple in calculation, the dynamic inverse solution plays a very important role in real-time force control of the multiaxial system. Real-time dynamics calculations are often a significant bottleneck when the multi-axis system is high in degrees of freedom, since the dynamic response of force control is typically required to be 5 to 10 times more frequent than that of motion control. On the one hand, due to the chain-of-axes inertia matrixNot only symmetrical, but also only in size of the conventional body chain inertia matrix 1/4, calculating the axis-chain generalized inertia matrix from equation (127)The amount of calculation is much smaller. On the other hand, the moving-axis axial inertial force is calculated from equation (126)The only calculation of (c) is 1/36 of newton's euler method.
Claims (9)
1. A tree chain robot dynamics and resolving method based on axis invariants is characterized by comprising the following steps:
given a multi-axis rigid system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F[i],The resultant force and moment acting on the axis u, in addition to gravity, are respectively recorded asi|DfuAndi|Dτu(ii) a The mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k of
According to the topological, structural and mass inertia parameters of the robot system, a Lagrange equation of a joint space is established by using a chain symbolic system, and a Curry-Kahn dynamics preparation equation is established based on the Lagrange equation of a multi-axis system;
substituting the deflection speed into an Cure-Kane dynamics preparatory equation to establish a tree chain rigid body system Cure-Kane dynamics equation;
establishing a tree chain rigid body system Jun-Kane normalized kinetic equation;
a Curry-Kahn dynamics preparatory equation is derived based on a multi-axis system Lagrange equation, and the method comprises the following steps:
【1】 The equivalence of a Lagrange equation and a Kane equation is proved;
【2】 Solving joint speed and coordinate bias speed based on energy based on Lagrange equation;
【3】 Calculating the derivative of the deflection speed to the time;
【4】 Obtaining a Jue-Kane dynamics preparatory equation based on the steps;
the method specifically comprises the following steps:
【1】 Proving the equivalence of the Lagrange equation and the Kane equation
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translational acceleration vector;is a translation velocity vector;is translational kinetic energy;is rotational kinetic energy;is a joint coordinate;is the joint velocity;
considering rigid k translation kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Considering rigid k rotational kinetic energy pairIs derived from the derivative of the yaw rate with respect to time
Due to the fact thatAnduncorrelated, from the Lagrangian equation of equation (7) and multiaxial systems
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is translational kinetic energy;is rotational kinetic energy;is gravitational potential energy;is a joint coordinate;is the joint velocity;
the translation kinetic energy and the rotation kinetic energy of the kinetic system D are respectively expressed as
Considering formula (4) and formula (5), namely, there are
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
the formula (7) and the formula (8) are the proof basis of the Ju-Kane dynamics preparation equation, namely the Ju-Kane dynamics preparation equation is essentially equivalent to the Lagrange method; meanwhile, the right side of the formula (8) comprises a multiaxial system Kane equation; the inertia force calculation of the Lagrange method and the Keynen method is consistent, namely the Lagrange method and the Keynen method are equivalent;
【2】 Based on Lagrange equation, joint velocity and coordinate bias velocity are obtained based on energy
Wherein:
[ 2-1 ] AAnd take into account Andonly with closed treeuL correlation, from formula (4) and formula (5)
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translation velocity vector;is a joint coordinate;is the joint velocity;
[ 2-2 ] AAnd take into account Andonly with closed treeuL correlation, from formula (4) and formula (5)
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a translation velocity vector;is the coordinate of the rotary joint;is the rotational joint speed;
【3】 Derivative of bias speed with respect to time
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd
【4】 The Jun-Kane dynamics preparatory equation is obtained based on the steps
The lie-kahn kinetics preparatory equation for axis u is
Equation (17) has a tree chain topology; k is a radical ofIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is a rotational velocity vector;is a rotational acceleration vector;is a translational acceleration vector;is a translation velocity vector;is a translational joint coordinate;is the translational joint speed;is the coordinate of the rotary joint;is the rotational joint speed; closed treeuThe generalized force in L is additive, the node of the closed subtree has only one kinematic chain to the root, the kinematic chainilnCan be used as a moving chainuL is replaced;
the resultant external force and moment acting on the shaft uThe components above are respectively noted asAndbilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe force and moment of environment i to axis are respectivelyAndiτl(ii) a Then the axial u-tree-chain rigid system is the equation of Keynes dynamics
Wherein: [. the]Representing taking a row or a column;andis a 3 x 3 block matrix,andis a 3D vector, q is joint space;
and is provided with a plurality of groups of the materials,
wherein, noteNote the book kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd an inertia matrix for the rotation axis u;an inertia matrix being a translation axis u; h isRA non-inertial matrix of rotation axis u; h isPA non-inertial matrix for the translational axis u;
definition of
The Jupiten normalized kinetic equation of the tree chain rigid system is as follows:
the canonical form of the formula (36) is
The canonical form of the formula (37) is
In the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd is an axis invariant;is the joint acceleration;as cross-multipliers, vectorsIs cross-multiplication matrix of To take from axis i to axisIs connected with the kinematic chainuL denotes obtaining a closed subtree consisting of the axis u and its subtree.
2. The axis-invariant based tree chain robot dynamics and solution method according to claim 1,
in the formula, along the axisPosition of the threadAround shaftAngular position ofAxial vectorAngular velocityLinear velocity
The left-order cross product and transposition relationship is:
3. The axis-invariant based tree chain robot dynamics and solution method according to claim 2, wherein,
given a point of application i in a free environment iSTo point l on axis lSDouble-sided external force ofAnd external momentiτlTheir instantaneous shaft power pexIs shown as
In the formula (26)And in formula (21)The chain sequences of (A) and (B) are different; the former is acting force, the latter is movement amount, the two are dual and have opposite orders;
Equations (26) and (27) show the resultant force or forces acting on axis k from the environmentMoment is equivalent to a closed treekL is the resultant force or moment on the axis k, and the expressions (26) and (27) are written together
4. The axis-invariant based tree chain robot dynamics and solution method according to claim 2, wherein,
if the shaft is a drive shaft, the drive force and drive torque of the shaft are respectivelyAnddriving forceAnd driving torqueGenerated power pacIs shown as
【1】 From formula (18), formula (19) and formula (29)
If the axis u is parallel to the axisIs coaxial, then hasNote the book Due to the fact thatAndindependently of each other, from the formula (30)
【2】 From formula (18), formula (19) and formula (29)
5. The axis-invariant based tree chain robot dynamics and solution method according to claim 1,
and (3) restating the tree chain rigid system Curie-Kane kinetic equation into a tree chain Curie-Kane normalized kinetic equation:
given a multi-axis rigid system D ═ a, K, T, NT, F, B }, the inertial system is denoted as F[i],The resultant force and moment acting on the axis u in addition to gravity isThe components above are respectively noted asAndthe mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAndacceleration of gravity of axis k ofBilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the moment of the environment i to the shaft are respectivelyAnd i τl(ii) a The Ju-Kane normalized kinetic equation of the axial u-tree rigid system is
and,
in the formula, kIRepresents the bar k centroid I; the mass of the axis k and the moment of inertia of the center of mass are respectively recorded as mkAnd an inertia matrix for the rotation axis u;an inertia matrix being a translation axis u; h isRA non-inertial matrix of rotation axis u; h isPA non-inertial matrix for the translational axis u; the resultant external force and moment acting on the shaft uThe components above are respectively noted asAnd bilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the acting moment of the environment i on the shaft are respectivelyAndiτl;llkto take the kinematic chain from axis l to axis k,ul denotes obtaining a closed subtree consisting of the axis u and its subtree.
6. The axis-invariant-based tree-chain robot dynamics and solution method according to claim 5, wherein,
and (3) given the generalized force of the environment action and the generalized driving force of the driving shaft, solving the acceleration or inertial acceleration of the dynamic system to obtain the positive solution of the Keynen dynamic equation of the tree-link rigid system.
7. The axis-invariant based tree chain robot dynamics and solution method of claim 6,
the specific steps of solving the positive solution of the tree chain rigid body system Cure-Kane kinetic equation are as follows:
Arranging all axis in-Kane dynamics standard equations in a system according to rows; the rearranged shaft driving generalized force and the immeasurable environmental acting force are recorded as fCMeasurable environmental generalized acting force is denoted as fi(ii) a The corresponding joint acceleration sequence is recorded asAfter rearrangementRecording as h; the system dynamics equation is
Is obtained by the formula (125)
The generalized inertia matrix of the system with the number of axes a is recorded as M3a′3a;
Axle chain generalized inertia matrixIs a symmetric matrix and it is a positive definite matrix, effectivelyThe calculation process is as follows:
【1】 First, LDL is applied to the resultantTThe decomposition is a matrix decomposition, i.e.,
Substituting formula (130) for formula (128)
Thus, a positive solution of the tree-chain rigid system Curt-Kane kinetic equation is obtained.
8. The axis-invariant-based tree-chain robot dynamics and solution method according to claim 5, wherein,
and solving the inverse solution of the tree chain rigid body system Cure-Kane kinetic equation.
9. The axis-invariant based tree chain robot dynamics and solution method of claim 8,
when the joint configuration, velocity and acceleration are known, the joint configuration is obtained by the formula (34)i|DfuAndi|Dτu(ii) a When the external force and the external moment are known, the driving force is solved by equation (132)And driving torque
Wherein the resultant force and moment acting on the axis u isThe components above are respectively noted asAnd bilateral driving force and driving torque of driving shaft uThe components above are respectively noted asAndthe acting force and the acting moment of the environment i on the shaft are respectivelyAndiτl;llkto take the kinematic chain from axis l to axis k,ul denotes obtaining a closed subtree consisting of the axis u and its subtree.
Priority Applications (2)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201810933332.3A CN109117451B (en) | 2018-08-16 | 2018-08-16 | Tree chain robot dynamics modeling and resolving method based on axis invariants |
| PCT/CN2018/112687 WO2020034405A1 (en) | 2018-08-16 | 2018-10-30 | Axis-invariant-based dynamics modeling and solving method for tree-chain robot |
Applications Claiming Priority (1)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN201810933332.3A CN109117451B (en) | 2018-08-16 | 2018-08-16 | Tree chain robot dynamics modeling and resolving method based on axis invariants |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN109117451A CN109117451A (en) | 2019-01-01 |
| CN109117451B true CN109117451B (en) | 2020-03-13 |
Family
ID=64853199
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN201810933332.3A Active CN109117451B (en) | 2018-08-16 | 2018-08-16 | Tree chain robot dynamics modeling and resolving method based on axis invariants |
Country Status (2)
| Country | Link |
|---|---|
| CN (1) | CN109117451B (en) |
| WO (1) | WO2020034405A1 (en) |
Families Citing this family (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN110532581B (en) * | 2019-05-14 | 2023-01-03 | 武汉弗雷德斯科技发展有限公司 | Dynamics modeling method of four-axis mechanical arm |
| CN119202499B (en) * | 2024-11-28 | 2025-03-14 | 湖南迈曦软件有限责任公司 | HINGE connector calculation method based on implicit flexible structure solver |
Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN103955611A (en) * | 2014-04-28 | 2014-07-30 | 西北工业大学 | Method for establishing universal mechanical model of tethered space robot |
| CN105956348A (en) * | 2016-06-29 | 2016-09-21 | 上海航天控制技术研究所 | Spacecraft dynamics modeling method |
| CN106295028A (en) * | 2016-08-16 | 2017-01-04 | 西北工业大学 | A kind of partial structurtes dynamic modeling method and device |
Family Cites Families (6)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US8924021B2 (en) * | 2006-04-27 | 2014-12-30 | Honda Motor Co., Ltd. | Control of robots from human motion descriptors |
| FR2978844B1 (en) * | 2011-08-04 | 2014-03-21 | Aldebaran Robotics | ROBOT WITH ARTICULATIONS OF VARIABLE RIGIDITY AND METHOD OF CALCULATING SAID OPTIMIZED RIGIDITY |
| CN104573255B (en) * | 2015-01-22 | 2017-10-31 | 天津理工大学 | It is a kind of to be modeled and method for solving based on the mechanical arm for improving multi-body system transfer matrix |
| CN107256284B (en) * | 2017-05-10 | 2022-06-21 | 中国北方车辆研究所 | Real-time interactive multi-gait dynamics modeling method and system for quadruped robot |
| CN107529630B (en) * | 2017-06-23 | 2021-06-29 | 西北工业大学 | A method for establishing dynamic model of space robot |
| CN108038286B (en) * | 2017-11-30 | 2021-12-03 | 长安大学 | Dynamics modeling method of two-degree-of-freedom redundant drive parallel robot |
-
2018
- 2018-08-16 CN CN201810933332.3A patent/CN109117451B/en active Active
- 2018-10-30 WO PCT/CN2018/112687 patent/WO2020034405A1/en active Application Filing
Patent Citations (3)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN103955611A (en) * | 2014-04-28 | 2014-07-30 | 西北工业大学 | Method for establishing universal mechanical model of tethered space robot |
| CN105956348A (en) * | 2016-06-29 | 2016-09-21 | 上海航天控制技术研究所 | Spacecraft dynamics modeling method |
| CN106295028A (en) * | 2016-08-16 | 2017-01-04 | 西北工业大学 | A kind of partial structurtes dynamic modeling method and device |
Non-Patent Citations (2)
| Title |
|---|
| 基于旋量理论凯恩动力学方程的开链机器人动力学分析;刘武发 等;《智能工程》;20070531;全文 * |
| 月面巡视器实时动力学建模与牵引控制;居鹤华 等;《宇航学报》;20140731;第35卷(第7期);全文 * |
Also Published As
| Publication number | Publication date |
|---|---|
| WO2020034405A1 (en) | 2020-02-20 |
| CN109117451A (en) | 2019-01-01 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| US11491649B2 (en) | Axis-invariant based multi-axis robot kinematics modeling method | |
| WO2020034420A1 (en) | Axis-invariant-based inverse kinematics modeling and solving method for multi-axis robot | |
| Orin et al. | Centroidal momentum matrix of a humanoid robot: Structure and properties | |
| WO2020034422A1 (en) | Axis-invariant-based forward kinematics modeling and solving method for multi-axis robot system | |
| WO2020034421A1 (en) | Axis-invariant-based modeling and control method for multi-axis robot system | |
| Kecskeméthy et al. | An object-oriented approach for an effective formulation of multibody dynamics | |
| CN107529630B (en) | A method for establishing dynamic model of space robot | |
| CN109117451B (en) | Tree chain robot dynamics modeling and resolving method based on axis invariants | |
| CN117921664A (en) | Seven-degree-of-freedom mechanical arm simulation method and system based on digital twin | |
| Altawil et al. | Design and analysis of a four dof robotic arm with two grippers used in agricultural operations | |
| CN109086544B (en) | Closed-chain robot dynamics modeling and resolving method based on axis invariant | |
| CN108959829B (en) | Non-ideal joint robot dynamics modeling method based on axis invariant | |
| Li et al. | Simulation and trajectory optimization of articulated robots via spectral variational integrators | |
| CN109015641B (en) | The inverse solution modeling of general 6R mechanical arm based on axis invariant and calculation method | |
| CN109033688B (en) | Inverse solution modeling and resolving method for universal 7R mechanical arm based on axis invariant | |
| CN108942943B (en) | Positive kinematics calculation method of multi-axis robot based on axis invariants | |
| CN108803350B (en) | Dynamic modeling and resolving method for movable base multi-axis robot based on axis invariants | |
| Li et al. | Dynamic modeling and analysis for 6-DOF industrial robots | |
| CN109079850B (en) | D-H system and D-H parameter determination method of multi-axis robot based on axis invariance | |
| CN108959828B (en) | Inverse solution modeling and resolving method for universal 3R mechanical arm based on axis invariant | |
| CN109291047A (en) | Based on axis invariant and the inverse solution modeling method of DH parameter 1R/2R/3R | |
| CN110597088A (en) | A Vehicle Dynamics Simulation Method in Polar Coordinate System | |
| Olaru et al. | Modeling and simulation of the parallel robot's structure with LabVIEW™ instrumentation | |
| WO2020034402A1 (en) | Axis-invariant-based accurate multi-axis robot structure parameter measurement method | |
| Silva et al. | Dynamic Modeling of Branched Robots using Modular Composition |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| PB01 | Publication | ||
| PB01 | Publication | ||
| SE01 | Entry into force of request for substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| GR01 | Patent grant |