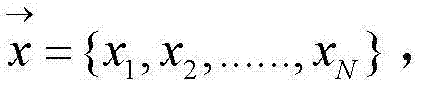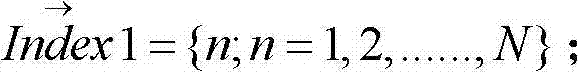CN101660945B - 快速图像重构方法 - Google Patents
快速图像重构方法 Download PDFInfo
- Publication number
- CN101660945B CN101660945B CN2009101479258A CN200910147925A CN101660945B CN 101660945 B CN101660945 B CN 101660945B CN 2009101479258 A CN2009101479258 A CN 2009101479258A CN 200910147925 A CN200910147925 A CN 200910147925A CN 101660945 B CN101660945 B CN 101660945B
- Authority
- CN
- China
- Prior art keywords
- wavelength
- prime
- interpolation
- image reconstruction
- lambda
- Prior art date
- Legal status (The legal status is an assumption and is not a legal conclusion. Google has not performed a legal analysis and makes no representation as to the accuracy of the status listed.)
- Expired - Fee Related
Links
- 238000000034 method Methods 0.000 title claims abstract description 48
- 239000013598 vector Substances 0.000 claims abstract description 24
- 239000011159 matrix material Substances 0.000 claims abstract description 15
- 238000012545 processing Methods 0.000 claims abstract description 7
- 230000008569 process Effects 0.000 claims description 8
- 238000012014 optical coherence tomography Methods 0.000 abstract description 6
- 230000003287 optical effect Effects 0.000 description 21
- 230000004048 modification Effects 0.000 description 4
- 238000012986 modification Methods 0.000 description 4
- 238000006243 chemical reaction Methods 0.000 description 2
- 238000001514 detection method Methods 0.000 description 2
- 238000010586 diagram Methods 0.000 description 2
- 230000000694 effects Effects 0.000 description 2
- 230000010287 polarization Effects 0.000 description 2
- 208000027418 Wounds and injury Diseases 0.000 description 1
- 230000008859 change Effects 0.000 description 1
- 238000011208 chromatographic data Methods 0.000 description 1
- 238000004587 chromatography analysis Methods 0.000 description 1
- 230000006378 damage Effects 0.000 description 1
- 238000002059 diagnostic imaging Methods 0.000 description 1
- 238000002474 experimental method Methods 0.000 description 1
- 238000000605 extraction Methods 0.000 description 1
- 208000014674 injury Diseases 0.000 description 1
- 238000013507 mapping Methods 0.000 description 1
- 230000007935 neutral effect Effects 0.000 description 1
- 230000003595 spectral effect Effects 0.000 description 1
- 238000006467 substitution reaction Methods 0.000 description 1
Images
Classifications
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
- G01B9/00—Measuring instruments characterised by the use of optical techniques
- G01B9/02—Interferometers
- G01B9/0209—Low-coherence interferometers
- G01B9/02091—Tomographic interferometers, e.g. based on optical coherence
-
- A—HUMAN NECESSITIES
- A61—MEDICAL OR VETERINARY SCIENCE; HYGIENE
- A61B—DIAGNOSIS; SURGERY; IDENTIFICATION
- A61B5/00—Measuring for diagnostic purposes; Identification of persons
- A61B5/72—Signal processing specially adapted for physiological signals or for diagnostic purposes
- A61B5/7235—Details of waveform analysis
- A61B5/7253—Details of waveform analysis characterised by using transforms
- A61B5/7257—Details of waveform analysis characterised by using transforms using Fourier transforms
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
- G01B9/00—Measuring instruments characterised by the use of optical techniques
- G01B9/02—Interferometers
- G01B9/02041—Interferometers characterised by particular imaging or detection techniques
- G01B9/02044—Imaging in the frequency domain, e.g. by using a spectrometer
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01B—MEASURING LENGTH, THICKNESS OR SIMILAR LINEAR DIMENSIONS; MEASURING ANGLES; MEASURING AREAS; MEASURING IRREGULARITIES OF SURFACES OR CONTOURS
- G01B9/00—Measuring instruments characterised by the use of optical techniques
- G01B9/02—Interferometers
- G01B9/02083—Interferometers characterised by particular signal processing and presentation
-
- A—HUMAN NECESSITIES
- A61—MEDICAL OR VETERINARY SCIENCE; HYGIENE
- A61B—DIAGNOSIS; SURGERY; IDENTIFICATION
- A61B5/00—Measuring for diagnostic purposes; Identification of persons
- A61B5/0059—Measuring for diagnostic purposes; Identification of persons using light, e.g. diagnosis by transillumination, diascopy, fluorescence
- A61B5/0062—Arrangements for scanning
- A61B5/0066—Optical coherence imaging
-
- G—PHYSICS
- G01—MEASURING; TESTING
- G01N—INVESTIGATING OR ANALYSING MATERIALS BY DETERMINING THEIR CHEMICAL OR PHYSICAL PROPERTIES
- G01N21/00—Investigating or analysing materials by the use of optical means, i.e. using sub-millimetre waves, infrared, visible or ultraviolet light
- G01N21/17—Systems in which incident light is modified in accordance with the properties of the material investigated
- G01N21/47—Scattering, i.e. diffuse reflection
- G01N21/4795—Scattering, i.e. diffuse reflection spatially resolved investigating of object in scattering medium
Landscapes
- Health & Medical Sciences (AREA)
- Physics & Mathematics (AREA)
- Engineering & Computer Science (AREA)
- Life Sciences & Earth Sciences (AREA)
- General Physics & Mathematics (AREA)
- General Health & Medical Sciences (AREA)
- Signal Processing (AREA)
- Biophysics (AREA)
- Medical Informatics (AREA)
- Computer Vision & Pattern Recognition (AREA)
- Physiology (AREA)
- Psychiatry (AREA)
- Mathematical Physics (AREA)
- Radiology & Medical Imaging (AREA)
- Nuclear Medicine, Radiotherapy & Molecular Imaging (AREA)
- Pathology (AREA)
- Biomedical Technology (AREA)
- Heart & Thoracic Surgery (AREA)
- Artificial Intelligence (AREA)
- Molecular Biology (AREA)
- Surgery (AREA)
- Animal Behavior & Ethology (AREA)
- Public Health (AREA)
- Veterinary Medicine (AREA)
- Investigating Or Analysing Materials By Optical Means (AREA)
- Length Measuring Devices By Optical Means (AREA)
- Instruments For Measurement Of Length By Optical Means (AREA)
- Complex Calculations (AREA)
Abstract
本发明提出了一种快速图像重构方法,事先通过傅立叶域光学相干层析系统特性对波长信息进行提取,得到一组在波数空间中均匀分布的波长向量,从而得到这个波长向量在CCD中的虚拟位置系数,由离散傅立叶变换补零插值传递函数产生加权系数矩阵,在系统运行时,由加权系数矩阵和采集到的数据进行插值或者对加权系数矩阵进行加窗截断后和采集到的数据进行插值,得到所要求的插值数据。本发明方法简单、易于实现,能够提高傅立叶域光学相干层析数据处理的精度和速度,提高了傅立叶域光学相干层析系统的实时图像重构能力。
Description
技术领域
本发明涉及一种快速图像重构方法,在所述快速图像重构方法中,采用了一种新型的、可用于傅立叶域光学相干层析等有插值需要的仪器的可变插值间隔的插值方法以及基于一切可利用的窗函数进行加窗截断的可变插值间隔的插值方法,从而实现快速图像重构。
背景技术
在快速图像重构领域,傅立叶域光学相干层析系统是一种新型的非接触、高分辨率的光学探测系统,它通过光学干涉的方法对目标进行纵向扫描,最后通过二维或三维重建,得出目标的结构信息、多普勒信息以及偏振信息,因此它可广泛应用于医学成像、各种工业损伤探测之中。傅立叶域光学相干层析技术中,参考光和信号光在光学分光器3中形成干涉,干涉信号由衍射光栅9进行分光,由透镜10聚焦到线扫描CCD11上,由CCD11将模拟信号转换为数字信号,如图2,光谱仪8由衍射光栅9,透镜10和线扫描CCD11构成;CCD11采集到的光栅出射波长按波长线性分布,但数据重建要求波长信息在k空间中线性分布,需要对数据进行插值。傅立叶域光学相干层析系统中可用于快速图像重构的插值方法有多种,如离散傅立叶变换补零插值,B样条拟合,直接线性插值等,而大多数的傅立叶域光学相干层析系统采用离散傅立叶变换补零插值和直接线性插值相结合的方法,即N点数据通过离散傅立叶变换运算之后,产生N点的频率域数据,在高频点补充M*N点的零值,产生M*N+N的数据,然后通过反傅立叶变换得到M*N+N点的数据,其中,M为补零的倍数,最后采用线性插值的方法得到N点的插值数据。由傅立叶域光学相干层析系统扫描采集的一组数据向量根据传统的离散傅立叶变换补零插的步骤为:
1)将数据进行离散傅立叶变换,得到一组新数据:
2)对新数据进行补零插值,得到M倍补零后的数据:
3)对M倍补零后的数据进行离散傅立叶逆变换,得到拓展了M+1倍后的数据;
4)对拓展后的数据根据线性分布K空间进行线性插值,可以得到插值后的数据。
这种方法简单,成熟,但具有运算量大,远远达不到实时图像重构的要求,插值间隔与插值精度由补零倍数M固定,不能随意改变插值间隔等缺点,并且由于进行离散傅立叶变换补零插值后再进行线性插值,因而插值精度也受到了影响,这些局限性严重制约了傅立叶域光学相干层析系统的快速图像重构应用。
发明内容
本发明要解决的技术问题是:克服现有傅立叶域光学相干层析技术的插值方法中插值精度低、运算速度慢,插值间隔固定且不能任意改变等问题,本发明提供一种快速图像重构方法,其中采用了一种新型的插值方法,该方法精度高,运算速度快,并具有可变的插值精度和插值间隔等特点,能有效得提高傅立叶域光学相干层析系统的运算速度和插值精度。
本发明解决其技术问题所采用的技术方案是:用于傅立叶域光学相干层析技术中可变插值间隔的插值方法以及利用一切可利用的窗函数进行加窗截断的可变插值间隔的插值方法。其特征在于以下步骤:
2)由第一个波长λ1和最后一个波长λN,利用公式k=2π/λ可以得到CCD 11首尾两像素点的波数k′1=2π/λ1和k′N=2π/λN,利用k′1和k′N组成一个长度为N的线性分布的波数向量 利用公式反算出相应的波长向量从而利用Δλ可以计算出每个波数k′n对应的λ′n在CCD11中的虚拟位置系数 (或者
4)傅立叶域光学相干层析系统中的CCD11采集一组纵轴扫描数据向量x={x1,x2,......,xN},进行数据插值,可到插值后的数据x′={xs1,xs2,......,xsN}。其计算公式如下
可以用一切可利用的窗函数对加权过程进行截断,根据窗长和 (或者 获得插值起始位置Min和结束位置Max,利用公式:
对原始数据进行插值,其中W(*)为所需加窗的窗函数,加窗窗长为L,从而提高新插值方法的运算速度。
在傅立叶域光学相干层析数据处理时,可以用一切可利用的窗函数对加权系数进行截断,将加权系数HN*N(n,sn)中的数据进行加窗截断,减少数据处理的数据处理长度和数据处理量。其计算公式如下:
公式中W(*)为一切可利用的加窗函数,插值运算起始位置Min和结束位置Max由加窗窗长L和虚拟位置系数 (或者 得到,从而提高可变插值间隔插值运算的处理速度,而且可以将加权系数存储在计算机中,方便运算时调用,避免重复计算。
另外,基于傅立叶变换过程中的能量守恒定律,可以对傅立叶补零插值进行如下修改:
相应地,由此得到改进后的傅立叶插值补零传递函数
另外,基于傅立叶变换过程中的和相等,也可以对傅立叶补零插值进行如下修改:
相应地,由此得到改进后的傅立叶插值补零传递函数
相应的加权系数矩阵HN*N(n,sn)。
本发明与现有技术相比有如下优点:
1.可在事前提取波长和波数信息,构造与K空间相对应的非线性分布波长向量以及这个波长向量在CCD11像素点所对应的虚拟位置系数向量,从而由传递函数计算出加权系数矩阵HN*N(n,sn),传统离散傅立叶变换补零值插的精度由补零倍数M固定,只能达到1/(M+1)的位置精度,因为虚拟位置系数sn的位置不是由传统离散傅立叶变换补零插值算法中的补零倍数M固定的,可以为计算机数据精度内的任意一个实数,从而实现可变的插值精度和插值间隔;
2.可利用一切可利用的加窗函数对加权系数矩阵进行加窗截取,并存储到计算机中,方便计算时调用,从而避免重复计算,由传统离散傅立叶变换补零插值方法中有一次N点和一次M*N+N点快速傅立叶变换,因此需要 次复数乘法,本方法仅需要N*L次实数乘法,其中,N为CCD11像素点数,L为加窗函数的窗长,从而提高插值方法的处理运算速度,提高离散傅立叶域光学相干层析系统的实时处理能力,由此能够实现快速图像重构。
附图说明
图1为傅立叶域光学相干层析系统数据插值流程图;
图2为傅立叶域光学相干层析系统结构图,其中1为光源,2为光学隔离器,3光学分光器,4为偏振控制器,5为PZT转换器,6为扫描控制器,7为采样目标,8为光谱仪,9为衍射光栅,10为透镜,11为线扫描CCD;
图3为插值效果比较图;
图4为二维图像重构。
具体实施方案
下面结合附图及具体实施方式详细介绍本发明。本实施方案采用的是傅立叶域光学相干层析系统,对其采集到的数据进行插值,其流程如图1所示;具体步骤如下:
(1)本实施方案从图2所示的光谱仪准确标定入射到CCD11的波长,中心波长为849.72nm,光谱分辨率Δλ=0.0674nm,线扫描CCD11上像素点数N=2048,CCD11上首尾两个像素点的波长分别为λ1=780.7024nm,λN=918.6702nm,各个波长在CCD11中位置系数为
由这个在K空间线性分布的波数向量通过公式得到一组非均匀的λ′={λ′1,λ′2,......,λ′N},显然,λ1=λ′1,λN=λ′N,从而可以利用公式计算波长λ′={λ′1,λ′2,......,λ′N}对应在CCD11中的虚拟位置系数 另外,关于sn的计算公式,也可以采用这样并不影响最终的技术效果,当然,相应地,波长λ′={λ′1,λ′2,......,λ′N}对应在CCD11中的虚拟位置系数也表示为 在以下的描述中,为简单、明了起见,将仅以上述第一种计算方式为例,进行描述,但这并不妨碍本发明采用第二种计算方式来实现,事实上,本发明也可以采用其他多种计算方式来实现;
(3)由实际波长在CCD11上位置系数向量
在CCD11的虚拟位置系数向量
(4)由图2所示的傅立叶域光学相干层析系统的CCD11采集到的一组干涉信号数据为x={x1,x2,......,xN},通过加窗长度为L=11的布莱克曼(Blackman)窗函数 l∈[0,L-1])截断加权系数,由插值公式得到插值之后的数据,其计算公式如下:
sn由 给出,
(5)对傅立叶域光学相干层析系统中CCD11采集到数据重复步骤(3)进行插值,由离散傅立叶变换对插值后的各组数据x′(s)进行傅立叶变换得到X′(s),令对比度Contrast=6,亮度偏差Brightness_Bias=-82,对X′(s)中的各个点进行对数运算可以得到图像的灰度值Intensity,其计算公式如下:
Intensity=Contrast*(10*log10(X′(s)+Brightness_Bias))+255
计算出灰度值还要进行截取,少于0的赋值为0,高于255的赋值为255,其目的是使其灰度范围在[0,255]之间,以符合计算机图像的灰度输出范围,由扫描控制器6对采样目标7重复线扫描,并对CCD11采集到的干涉信号数据中进行插值和映射,重构出二维图像或都三维图像,图4为一张重构的二维图像。
为了对比,在实施本方案的同时,运用传统的离散傅立叶变换补零插值方法,在本次实验中,取一组线扫描数据4倍抽取后再进行插值,插值后的数据如图3所示,与原始数据相减后,新方法均值为0.1409,方差为0.2524,传统的离散傅立叶变换补零方法均值为0.1448,方差为0.2564。可见均值和方差的对比均为基于可变间隔的插值方法的为佳。用傅立叶域光学相干层析系统对一物体进行扫描,采集到2048*300的数据进行处理及重构图像,重构后的图像如图4。在CPU为酷睿Q9300,内存为4GB时,运算时间由原来的9秒减少到目前的400毫秒,大大提高了处理速度。
基于傅立叶变换过程中的能量守恒定律,可以对傅立叶补零插值进行如下修改:
相应地,由此得到改进后的傅立叶插值补零传递函数
相应的加权系数矩阵HN*N(n,sn)。
基于傅立叶变换过程中的和相等,也可以对傅立叶补零插值进行如下修改:
相应地,由此得到改进后的傅立叶插值补零传递函数
相应的加权系数矩阵HN*N(n,sn)。
虽然通过参照本方法的说明和具体实施方案,已经对本方法进行了图示和描述,但普通的技术人员应该明白,可以在形式上和细节上对其作各种各样的改变,而不偏离所附权利要求书所限定的本方法的精神和范围。
Claims (8)
1.一种快速图像重构方法,包括以下步骤:
将在波数空间中、均匀分布在与最短波长λ1相对应的波数和与最长波长λN相对应的波数之间的波数向量转换为一组在波长空间中非均匀分布的波长向量并根据上述波长差Δλ,得到波长向量的各个波长在CCD(11)中的虚拟位置系数
在CCD(11)采集到一组数据向量x={x1,x2,……,xN}时,利用加权系数矩阵HN*N(n,sn),对数据向量x={x1,x2,……,xN}进行插值处理,得到插值后的数据 以及
对插值后的数据进行离散傅立叶变换,实现图像重构,
其中
Intensity=Contrast*(10*log10(X′(sn)+Brightness_Bias))+255,
其中Intensity表示灰度值,Contrast表示对比度,Brightness_Bias表示亮度偏差,
如果得到的灰度值Intensity小于0,则为Intensity赋值0;以及如果得到的灰度值Intensity大于255,则为Intensity赋值255。
2.根据权利要求1所述的快速图像重构方法,其中所述补零插值传递函数是根据下述公式得到的:
3.根据权利要求1所述的快速图像重构方法,其中所述补零插值传递函数是根据下述公式得到的:
4.根据权利要求1所述的快速图像重构方法,其中所述补零插值传递函数是根据下述公式得到的:
7.根据权利要求1所述的快速图像重构方法,其中
除了利用加权系数矩阵HN*N(n,sn)外,还同时利用窗函数对加权系数矩阵HN*N(n,sn)进行加窗截断后对数据向量x={x1,x2,……,xN}进行插值处理。
8.根据权利要求7所述的快速图像重构方法,其中
对数据向量x={x1,x2,……,xN}的插值处理是根据下述公式执行的:
其中W(*)是窗函数,Max和Min的值由窗函数的加窗长度和各个虚拟位置共同确定。
Priority Applications (4)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CN2009101479258A CN101660945B (zh) | 2008-08-27 | 2009-06-10 | 快速图像重构方法 |
| JP2009176314A JP5281511B2 (ja) | 2008-08-27 | 2009-07-29 | 高速画像再構築方法 |
| US12/538,006 US8189958B2 (en) | 2008-08-27 | 2009-08-07 | Method of fast image reconstruction |
| DE102009038889A DE102009038889B4 (de) | 2008-08-27 | 2009-08-26 | Verfahren zur schnellen Bildrekonstruktion |
Applications Claiming Priority (3)
| Application Number | Priority Date | Filing Date | Title |
|---|---|---|---|
| CNA2008101191316A CN101358879A (zh) | 2008-08-27 | 2008-08-27 | 傅立叶域光学相干层析技术中可变插值间隔的插值方法 |
| CN200810119131.6 | 2008-08-27 | ||
| CN2009101479258A CN101660945B (zh) | 2008-08-27 | 2009-06-10 | 快速图像重构方法 |
Publications (2)
| Publication Number | Publication Date |
|---|---|
| CN101660945A CN101660945A (zh) | 2010-03-03 |
| CN101660945B true CN101660945B (zh) | 2013-02-20 |
Family
ID=41725560
Family Applications (1)
| Application Number | Title | Priority Date | Filing Date |
|---|---|---|---|
| CN2009101479258A Expired - Fee Related CN101660945B (zh) | 2008-08-27 | 2009-06-10 | 快速图像重构方法 |
Country Status (4)
| Country | Link |
|---|---|
| US (1) | US8189958B2 (zh) |
| JP (1) | JP5281511B2 (zh) |
| CN (1) | CN101660945B (zh) |
| DE (1) | DE102009038889B4 (zh) |
Families Citing this family (11)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US9014492B2 (en) | 2012-10-23 | 2015-04-21 | The Boeing Company | Real-time image reconstruction |
| CN103325091B (zh) * | 2013-03-07 | 2016-02-17 | 上海交通大学 | 低频频谱数据补零法图像获取方法及系统 |
| US11249759B2 (en) | 2013-07-15 | 2022-02-15 | Texas Instruments Incorporated | Two-dimensional zero padding in a stream of matrix elements |
| US11113062B2 (en) | 2013-07-15 | 2021-09-07 | Texas Instruments Incorporated | Inserting predefined pad values into a stream of vectors |
| US11231929B2 (en) | 2013-07-15 | 2022-01-25 | Texas Instruments Incorporated | One-dimensional zero padding in a stream of matrix elements |
| CN104236710B (zh) * | 2014-09-29 | 2015-12-02 | 杭州彩谱科技有限公司 | 一种手持式光源颜色照度测量仪的光谱超分辨方法 |
| CN105816151B (zh) * | 2016-03-10 | 2018-08-07 | 天津大学 | 一种基于空间频域测量的均匀组织体光学参数重建方法 |
| CN106872407B (zh) * | 2017-03-07 | 2019-04-19 | 中国科学院上海光学精密机械研究所 | 一种提高扫频光学相干层析成像分辨率方法 |
| US10718860B2 (en) * | 2018-01-11 | 2020-07-21 | Infineon Technologies Ag | System and method to improve range accuracy in FMCW radar using FSK modulated chirps |
| JP7581674B2 (ja) | 2020-07-03 | 2024-11-13 | 株式会社ニデック | Oct装置 |
| CN111461961B (zh) * | 2020-03-27 | 2022-10-21 | 佛山市灵觉科技有限公司 | 一种oct血管图像错位矫正方法 |
Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN1397255A (zh) * | 2001-07-13 | 2003-02-19 | 株式会社岛津制作所 | 图像重构方法、图像重构软件及所用记录介质和射线照相装置 |
| CN1602811A (zh) * | 2003-09-29 | 2005-04-06 | Ge医疗系统环球技术有限公司 | 图像重构、投影数据评价方法及计算x线体层照相装置 |
Family Cites Families (13)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| US4562540A (en) * | 1982-11-12 | 1985-12-31 | Schlumberger Technology Corporation | Diffraction tomography system and methods |
| JPS62217730A (ja) * | 1986-03-19 | 1987-09-25 | Fujitsu Ltd | 周波数圧伸方式 |
| JPH01320409A (ja) * | 1988-06-22 | 1989-12-26 | Toray Ind Inc | 膜厚測定方法 |
| JP2762775B2 (ja) * | 1990-06-22 | 1998-06-04 | 松下電器産業株式会社 | 分光測定方法 |
| US6748098B1 (en) * | 1998-04-14 | 2004-06-08 | General Electric Company | Algebraic reconstruction of images from non-equidistant data |
| JP3536778B2 (ja) | 2000-05-10 | 2004-06-14 | 日本電気株式会社 | ネットワーク及びそれに用いる帯域保証方法 |
| JP2003076385A (ja) * | 2001-08-31 | 2003-03-14 | Tama Tlo Kk | 信号分析方法および信号分析装置 |
| JP3866211B2 (ja) | 2002-12-26 | 2007-01-10 | 本田技研工業株式会社 | アクチュエータの制御装置 |
| CN103082996A (zh) * | 2003-10-27 | 2013-05-08 | 通用医疗公司 | 用于使用频域干涉测量法进行光学成像的方法和设备 |
| CN101023376B (zh) * | 2004-07-23 | 2011-05-18 | 比约恩·A·J·安杰尔森 | 超声成像 |
| US7683827B2 (en) * | 2004-12-15 | 2010-03-23 | Valeo Radar Systems, Inc. | System and method for reducing the effect of a radar interference signal |
| JP4421487B2 (ja) * | 2005-01-26 | 2010-02-24 | 株式会社東芝 | 送信信号生成装置、信号処理装置及びアンテナ装置 |
| EP2049019A4 (en) * | 2006-08-03 | 2011-11-30 | Univ California | ITERATIVE METHOD FOR DOSE REDUCTION AND IMAGE ENLARGEMENT IN TOMOGRAPHY |
-
2009
- 2009-06-10 CN CN2009101479258A patent/CN101660945B/zh not_active Expired - Fee Related
- 2009-07-29 JP JP2009176314A patent/JP5281511B2/ja not_active Expired - Fee Related
- 2009-08-07 US US12/538,006 patent/US8189958B2/en active Active
- 2009-08-26 DE DE102009038889A patent/DE102009038889B4/de not_active Expired - Fee Related
Patent Citations (2)
| Publication number | Priority date | Publication date | Assignee | Title |
|---|---|---|---|---|
| CN1397255A (zh) * | 2001-07-13 | 2003-02-19 | 株式会社岛津制作所 | 图像重构方法、图像重构软件及所用记录介质和射线照相装置 |
| CN1602811A (zh) * | 2003-09-29 | 2005-04-06 | Ge医疗系统环球技术有限公司 | 图像重构、投影数据评价方法及计算x线体层照相装置 |
Non-Patent Citations (3)
| Title |
|---|
| 张地 等.大倍数超分辨率图像重构的通用快速算法.《华南理工大学学报(自然科学版)》.2004,第32卷(第11期), * |
| 段海峰 等.快速傅里叶算法在哈特曼-夏克传感器波前重构算法中的应用.《光学学报》.2003,第23卷(第2期), * |
| 马社祥 等.基于三次样条插值的图像多尺度方向边缘重构.《光学与光电技术》.2005,第3卷(第6期), * |
Also Published As
| Publication number | Publication date |
|---|---|
| CN101660945A (zh) | 2010-03-03 |
| JP5281511B2 (ja) | 2013-09-04 |
| US20100054626A1 (en) | 2010-03-04 |
| JP2010054501A (ja) | 2010-03-11 |
| DE102009038889B4 (de) | 2013-08-08 |
| DE102009038889A1 (de) | 2010-05-27 |
| US8189958B2 (en) | 2012-05-29 |
Similar Documents
| Publication | Publication Date | Title |
|---|---|---|
| CN101660945B (zh) | 快速图像重构方法 | |
| US9404730B2 (en) | Methods for processing images generated using fourier domain optical coherence tomography (FDOCT) | |
| CN107247332B (zh) | 一种基于散斑估计和反卷积的非侵入式散射成像方法 | |
| CN108319009A (zh) | 基于结构光调制的快速超分辨成像方法 | |
| CN107084789A (zh) | 基于稀疏先验的单像素探测器光谱反射率重构方法 | |
| CN110333189A (zh) | 基于压缩感知原理的光子集成干涉成像高分辨重构方法 | |
| CN105030201A (zh) | 基于静态区域信息的扫频oct数字相位矫正方法与系统 | |
| CN116091368B (zh) | 一种色散补偿方法、装置、电子设备及存储介质 | |
| CN116482317A (zh) | 湖泊水体营养状态实时监测方法、系统、设备及介质 | |
| CN113839711A (zh) | 一种基于动态阈值距离质心算法的峰值检测方法 | |
| CN101358879A (zh) | 傅立叶域光学相干层析技术中可变插值间隔的插值方法 | |
| CN114894793B (zh) | 基于消除伪影的成像方法、成像系统及服务器 | |
| CN106556340A (zh) | 基于调制度的宽光谱干涉的零级条纹的寻找方法 | |
| CN109443250A (zh) | 一种基于s变换的结构光三维面形垂直测量方法 | |
| CN112697269A (zh) | 一种基于模拟声场先验信息的声强稀疏测量高分辨率成像方法 | |
| CN111829954B (zh) | 一种提高全场扫频光学相干层析测量量程的系统及方法 | |
| CN116612170A (zh) | 光学相干层析应变场的复矢量估计方法、设备及存储介质 | |
| Klein | Multispectral imaging and image processing | |
| CN106504195B (zh) | 超分辨成像方法和等光程及非等光程超分辨成像系统 | |
| CN108387326B (zh) | 极轨卫星高分辨率卫星资料条纹噪音滤除方法 | |
| Ahmad et al. | Interferometric synthetic aperture microscopy implementation on a floating point multi-core digital signal processer | |
| CN114972094B (zh) | 一种基于全尺度回归的高通调制全色锐化方法及装置 | |
| CN111063022A (zh) | 一种结合相位梯度与直接线性变换的相位体三维重建法 | |
| Aja-Fernandez et al. | Return-to-the-origin probability calculation in single shell acquisitions | |
| CN114518654B (zh) | 一种高分辨大景深成像方法 |
Legal Events
| Date | Code | Title | Description |
|---|---|---|---|
| C06 | Publication | ||
| PB01 | Publication | ||
| C10 | Entry into substantive examination | ||
| SE01 | Entry into force of request for substantive examination | ||
| C14 | Grant of patent or utility model | ||
| GR01 | Patent grant | ||
| CF01 | Termination of patent right due to non-payment of annual fee | ||
| CF01 | Termination of patent right due to non-payment of annual fee |
Granted publication date: 20130220 |