Clean tile is a game investigated by Buffon (1777) in which players bet on the number of different tiles a thrown coin will partially cover on a floor that is regularly
tiled. Buffon investigated the probabilities on a triangular
grid, square grid, hexagonal
grid, and grid composed of rhombi. Assume that the
side length of the tile is greater than the coin diameter
. Then, on a square grid, it is possible for a coin to land
so that it partially covers 1, 2, 3, or 4 tiles. On a triangular grid, it can land
on 1, 2, 3, 4, or 6 tiles. On a hexagonal grid, it can land on 1, 2, or 3 tiles.
Special cases of this game give the Buffon-Laplace needle problem (for a square grid) and Buffon's needle problem (for infinite equally spaced parallel lines).
|
|
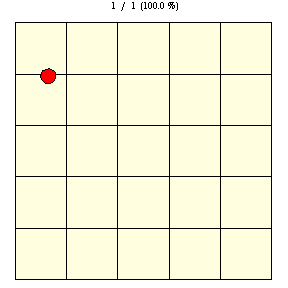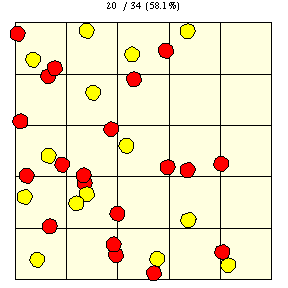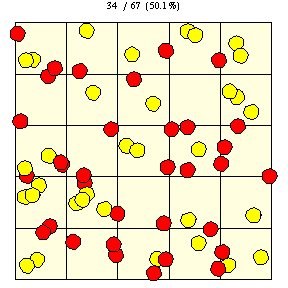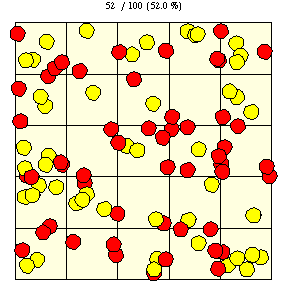
|
As shown in the figure above, on a square grid with tile edge length ,
the probability that a coin of diameter
will lie entirely on a single tile (indicated by yellow disks
in the figure) is given by
|
(1)
|
since the shortening of the side of a square obtained by insetting from a square of side length
by the radius of the coin
is given by
|
(2)
|
The probability that it will lie on two or more (indicated by red disks) is just
|
(3)
|
For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives
|
(4)
|
The probability of landing on exactly two tiles is the ratio of shaded area in the above figure to the tile size, namely
|
(5)
| |||
|
(6)
|
On a square grid, the probability of a coin landing on exactly three tiles is the fraction of a tile covered by the region illustrated in the figure above,
|
(7)
|
Similarly, the probability of a coin landing on four tiles is the fraction of a tile covered by a disk, as illustrated in the figure above,
|
(8)
|
|
|
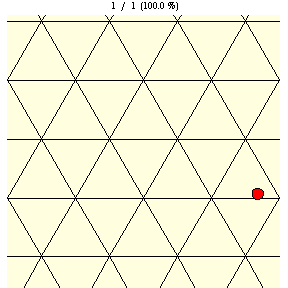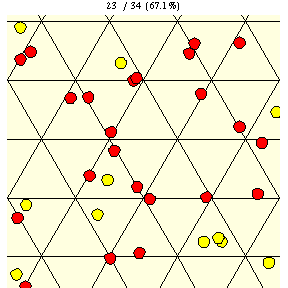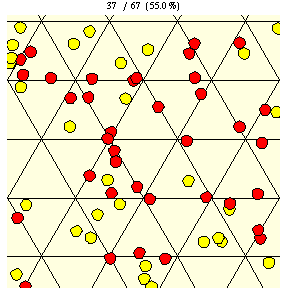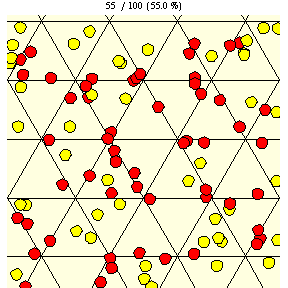
|
As shown in the figure above, on a triangular grid with tile edge length , the probability that a coin of diameter
will lie entirely on a single tile is given by
|
(9)
|
since the shortening of the side of an equilateral triangle obtained by insetting from a triangle of side length by the radius of the coin
is
|
(10)
|
The probability that it will lie on two or more is just
|
(11)
|
For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives
|
(12)
|
As shown in the figure above, on a hexagonal grid with tile edge length , the probability that a coin of diameter
will lie entirely on a single tile is given by
|
(13)
|
since the shortening of the side of a regular hexagon obtained by insetting from a triangle of side length by the radius of the coin
is
|
(14)
|
The probability that it will lie on two or more is just
|
(15)
|
For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives
|
(16)
|
In a quadrilateral tiling formed by rhombi with opening angle ,
insetting from a rhombus of side length
gives
|
(17)
| |||
|
(18)
|
so
|
(19)
|
Therefore, the probability that a coin will lie on a single tile is
|
(20)
| |||
|
(21)
|
The probability that it will lie on two or more is just
|
(22)
|
For the game to be fair with two players betting on (1) a single tile or (2) two or more tiles, these quantities must be equal, which gives
|
(23)
|
As expected, this reduces to the square case for .