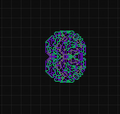
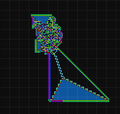
הנמלה של לנגטון

הנמלה של לנגטון אחרי 11,000 צעדים. הנקודה האדומה מראה את מיקום הנמלה.

הנמלה של לנגטון היא מכונת טיורינג דו-ממדית עם סט פשוט מאוד של כללי התנהגות אבל תוצאה מורכבת. היא הומצאה על ידי כריס לנגטון בשנת 1986 ופועלת על סריג מרובע של תאים שחורים ולבנים. בשנת 2000 הוכח כי הנמלה של לנגטון היא שלמה-טיורינג, כלומר בכוחה לדמות מכונת טיורינג כלשהי. לנמלה של לנגטון יש גרסאות שונות, כגון טיורמיטים שמוסיפים יותר צבעים ויותר מצבים.

חוקים

אנימציה של 200 הצעדים הראשונים של הנמלה של לנגטון

• בריבוע לבן הנמלה פונה 90° ימינה, מחליפה את הצבע של המשבצת שעליה היא עומדת ונעה משבצת אחת קדימה.
• בריבוע שחור הנמלה פונה 90° שמאלה, מחליפה את הצבע של המשבצת שעליה היא עומדת ונעה משבצת אחת קדימה.

הנמלה של לנגטון יכולה להיות מתוארת גם כאוטומט תאי, שבו הרשת היא בצבעים שחור או לבן ויש לו את המרובע "הנמלה" שהוא אחד משמונה צבעים שונים שהוקצו לשינוי השילוב של המשבצות וכיוון תנועה נוכחי.

מצבי התנהגות

כללים פשוטים אלה מובילים להתנהגויות מורכבות. כאשר מתחילים ברשת לבנה לחלוטין ניתן לזהות שלושה מצבי התנהגות המתרחשים זה לאחר זה:

1. פשטות. במהלך כמה מאות המהלכים הראשונים שלה הנמלה יוצרת דפוסים מאוד פשוטים ולעיתים קרובות סימטריים.
2. כאוס. לאחר כמה מאות מהלכים, דפוס גדול ולא סדיר של ריבועים שחורים ולבנים מופיע. מסלול הנמלה נראה לכאורה אקראי עד לכ-10,000 צעדים.
3. סדר מתהווה. לבסוף הנמלה מתחילה לבנות דפוס חוזר ונשנה, המכונה "כביש", של 104 צעדים שחוזרים על עצמם זמן בלתי מוגבל.

כל התצורות הראשוניות הסופיות שנבדקו הגיע בסופו של דבר לאותו דפוס חוזר על עצמו, המצביעות על כך ש"הכביש" הוא המשכה של כל מסלול של הנמלה של לנגטון, אבל אף אחד לא הצליח להוכיח שזה נכון לכל התצורות הראשוניות. ידוע רק שהמסלול של הנמלה הוא תמיד חסר גבולות, ללא קשר לתצורה הראשונית - דבר זה ידוע כמשפט כהן-קונג.

גרסאות במספר רב של צבעים

גרג טורק וג'ים פרופן חשבו על הרחבה פשוטה של הנמלה של לנגטון. במקום שני צבעים ניתן לשים כל מספר של צבעים, כשסדר הצבעים מחזורי, ופיתחו שיטה פשוטה למתן שמות: לכל אחד מהצבעים ניתנת אות "L" או "R" שמסמלות את כיוון התנועה של הנמלה. לפי שיטה זו הנמלה של לנגטון היא "RL". חלק מהנמלים של לנגטון בשיטה זו יוצרים דפוסים סימטריים פעם אחר פעם. אחת הדוגמאות הפשוטות לנמלה כזו היא הנמלה "RLLR". תנאי אחד היוצר מצב זה הוא שהשם של הנמלה נראה כרשימה מחזורית, כלומר שהוא מורכב מזוגות רצופים של "LL" או "RR".

• דפוסי דוגמה של גרסאות מרובות צבע של הנמלים של לנגטון:
• 
  RLR: גדל בתוהו ובוהו. לא ידוע אם נמלה זו מייצרת אי פעם "כביש".
• 
  LLRR: גדל באופן סימטרי.
• 
  LRRRRRLLR: ממלא את חלל המרצפות סביב עצמו.
• 
  LLRRRLRLRLLR: יוצר כביש מפותל.
• 
  RRLLLRLLLRRR: יוצר צורה של משולש מלא שגדל וזז.
• 
  L2NNL1L2L1: יוצר רשת משושה, גדלה במעגל.
• 
  L1L2NUL2L1R2: יוצר רשת משושה, צמיחה בספירלה.

טיורמיטים 

ערך מורחב – טיורמיט

גרסה נוספת של הנמלים של לנגטון היא לאפשר מצבים מרובים של מכונות טיורינג - כאילו לנמלה עצמה יש צבע שיכול להשתנות. נמלים אלו נקראות טיורמיטים, הלחם של "טרמיטי מכונת טיורינג" (באנגלית:"Turing machine termites"). התנהגויות נפוצות שלהם כוללות יצירת כבישים, צמיחה של כאוס וצמיחה בספירלה.

• דוגמאות לטיורמיטים:
• 
  צמיחה ספירלית
• 
  ייצור של כביש לאחר תקופה של צמיחה כאוטית.
• 
  צמיחה של תוהו ובוהו עם מרקם ייחודי.
• 
  צמיחה עם מרקם ייחודי תוך כדי הרחבת המסגרת.
• 
  בניית ספירלת פיבונאצ'י.

גרסאות במספר רב של נמלים

מספר רב של נמלים של לנגטון יכולות להתקיים במישור דו־ממדי יחדיו, ויכולות ליצור יחד אוטומטים שבונים מספר רב של בניינים מורכבים. אין צורך לפתור בעיות כגון הימצאות שתי נמלים באותה המשבצת, מכיוון ששתיהן משנות את המשבצת באותה הצורה.

טיורמיטים מרובים יכולים להתקיים במישור דו־ממדי יחדיו, כל עוד יוצרים כללים למקרה בו הם נפגשים. אד פג' ג'וניור המציא גרסה שבה הנמלים יכולות לפנות גם ימינה וגם שמאלה, יש נמלים שיכולות להתפצל ויש נמלים שמשמידות אחת את השנייה כשהם נפגשות.

ראו גם

• משחק החיים (אוטומט תאי)
• טיורמיט
• התולעים של פטרסון

קישורים חיצוניים

מדיה וקבצים בנושא הנמלה של לנגטון בוויקישיתוף

• ויסטן, אריק וו, "הנמלה של לנגטון", באתר MathWorld (באנגלית)
• סימולציה של מגוון תצורות הנמלה של לנגטון, סרטון באתר יוטיוב
• הפעלה אונליין של מספר רב של נמלים
• כריס לנגטון מדגים  אינטראקציה של מספר נמלים ב"מושבה", סרטון באתר יוטיוב (באנגלית)
• סימולציה של מספר רב של נמלים
• סימולציה של נמלה אחת עם אפשרות לצביעת הלוח
• סימולציה רבת אפשרויות (כולל מספר צבעים) של נמלה
• הנמלה של לנגטון, באתר MathWorld (באנגלית)