Deep learning is a powerful technique within the broader field of machine learning, where models known as neural networks are used to learn from data. These networks can uncover complex relationships and patterns, making them ideal for tasks such as image recognition, natural language processing, and function approximation.
A neural network is a system of interconnected nodes, or "neurons," arranged in layers. Each neuron receives input, processes it through a series of mathematical operations, and produces an output. This output then serves as input to the next layer in the network, allowing the model to progressively build up more complex representations of the data.
- Input Layer: This is where the model receives its data.
- Hidden Layers: These layers apply activation functions to the input, transforming it in ways that enable the network to learn.
- Output Layer: The final layer produces the network's prediction.
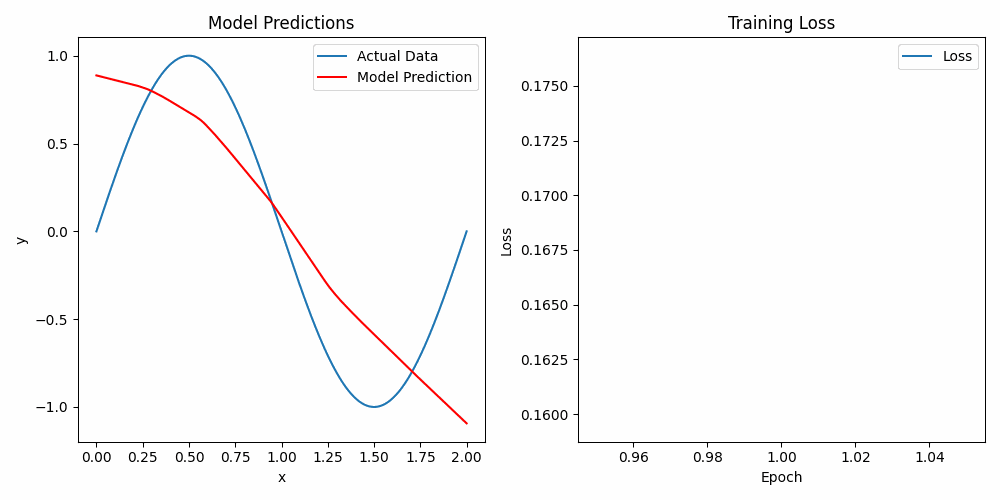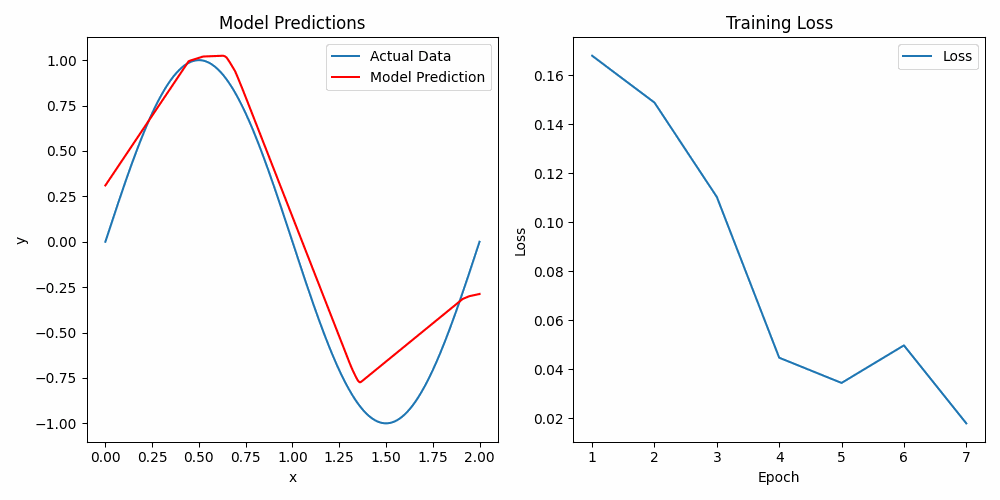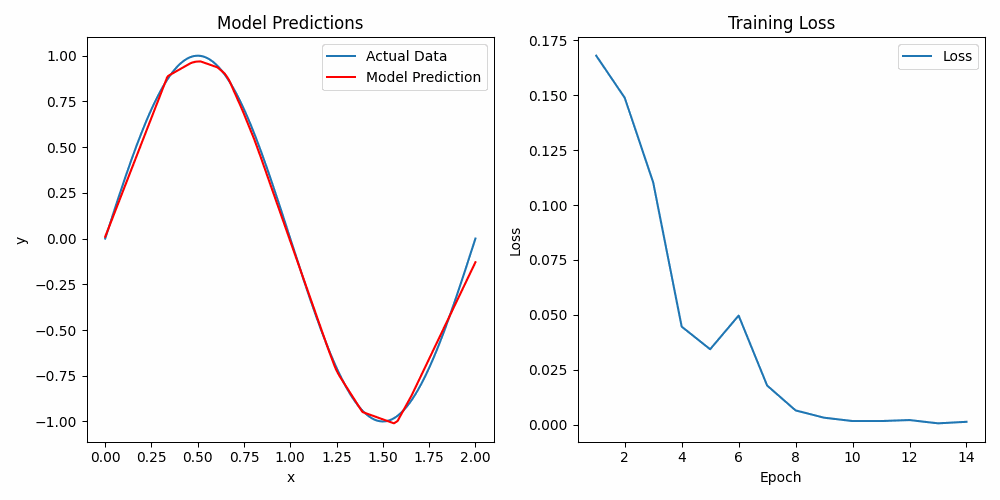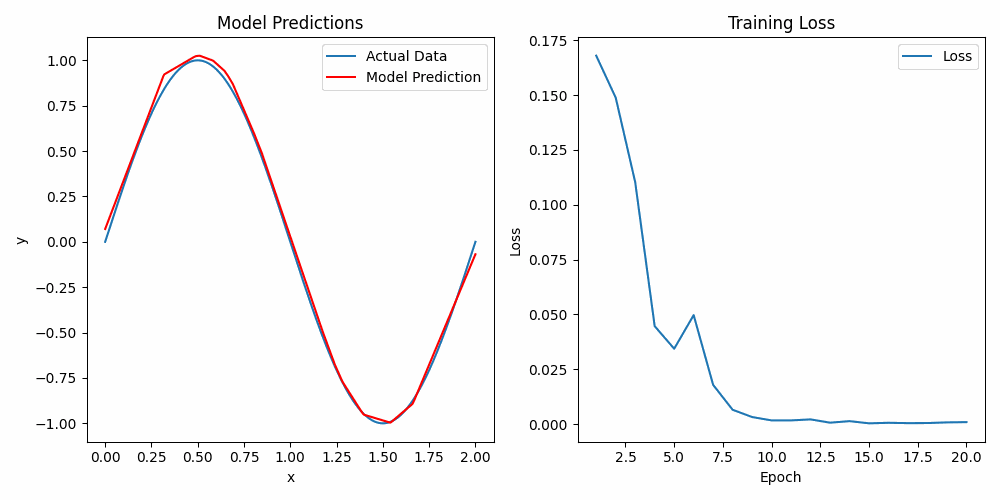
This example is designed to provide a basic understanding of deep learning concepts by walking through the process of predicting a sine function using a neural network. We'll explore how to set up a simple model, understand its components, and see it in action using both PyTorch and TensorFlow.
Predicting the sine function is a classic problem that helps illustrate how neural networks work in a simple and intuitive way. Despite its simplicity, the sine function has enough complexity to demonstrate key deep learning concepts such as activation functions.
Figure 2 visualizes how the activation function influences the learning process of the neural network when approximating the sine function. The curve shown highlights key points where the network has learned the underlying pattern of the sine wave. These specific points, where the curve changes more noticeably, correspond to activation points where the ReLU function behaves similarly to an "if" statement. In these regions, the ReLU activation either allows the signal to pass through or blocks it, depending on whether the input is positive or negative, thus shaping the curve accordingly.
One of the most important components of a neural network is the activation function. After a neuron computes its weighted sum of inputs, the activation function decides whether that neuron should "fire" (send its signal forward) or not. This is akin to an "if" statement in programming:
-
ReLU (Rectified Linear Unit): A popular activation function that outputs the input directly if it's positive; otherwise, it outputs zero. This introduces non-linearity, enabling the network to learn from complex data patterns.
-
Sigmoid: The Sigmoid activation function maps the input to a value between 0 and 1 using the formula
$\sigma(x) = \frac{1}{1 + e^{-x}}$ . It is often used in the output layer of binary classification models because it can represent a probability. However, it can suffer from the vanishing gradient problem, especially for very large or small input values, which can slow down learning. -
Tanh (Hyperbolic Tangent): The Tanh function is similar to the Sigmoid function but maps the input to a value between -1 and 1 using the formula
$\text{tanh}(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}$ . It is centered around zero, which makes it often preferred over the Sigmoid function as it tends to produce outputs with stronger gradients. However, like Sigmoid, it can also suffer from the vanishing gradient problem for very large or small input values.
The PyTorch implementation defines a custom model class and uses a training loop to optimize the model parameters. The code for this implementation can be found here.
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.fc1 = torch.nn.Linear(1, 50)
self.fc2 = torch.nn.Linear(50, 50)
self.fc3 = torch.nn.Linear(50, 1)
def forward(self, x):
x = torch.relu(self.fc1(x))
x = torch.relu(self.fc2(x))
x = self.fc3(x)
return xThe TensorFlow implementation uses the Sequential API to build the model and the fit method for training. The code for this implementation can be found here.
model = tf.keras.Sequential([
tf.keras.layers.Dense(50, activation='relu', input_shape=(1,)),
tf.keras.layers.Dense(50, activation='relu'),
tf.keras.layers.Dense(1)
])One of the most prominent limitations of a linear model is its inability to solve the XOR problem. While a linear model can handle AND and OR operations, it fails with the XOR operation. In the study of AI, it is commonly known that a Multilayer Perceptron (MLP) can solve the XOR problem. This document explores how this is achieved.
When classifying data, a linear model can only create a linear boundary, effectively dividing data into two categories using a straight line. This approach works for operations like AND and OR, where a linear line can separate the outputs (0 and 1). However, the XOR operation is not linearly separable, meaning a single straight line cannot separate the outputs for XOR.
This limitation of the perceptron was mathematically demonstrated by Marvin Minsky and Seymour Papert in their book Perceptrons: An Introduction to Computational Geometry (1969).
2.2. Solving XOR with a Hidden Layer
To solve the XOR problem, at least two lines or a non-linear boundary are required. In this document, we demonstrate how two lines can be used to solve the XOR problem.
Conceptually, the XOR operator can be represented by the intersection of two logical operations:
- NOT (x1 AND x2) - A line representing this operation.
- (x1 OR x2) - A line representing this operation.
The intersection of these two lines (AND operation) yields a result of 1 where the XOR condition is met, and 0 otherwise. In the figure, the blue line represents the NAND operation, and the orange line represents the OR operation.
To classify XOR, the input layer must consist of neurons corresponding to the input pairs (0,0), (0,1), (1,0), and (1,1). Therefore, the input layer contains two neurons. The hidden layer needs at least two neurons to form the two lines necessary for classification. These neurons are fully connected (FC) and use weights, biases, and the Sigmoid activation function.
The Sigmoid function is used as the activation function. It approaches 1 as the input becomes more positive and 0 as the input becomes more negative.
# Define the neural network model
model = tf.keras.Sequential([
# Fully connected layer with sigmoid activation
tf.keras.layers.Dense(2, activation="sigmoid", input_shape=(2,)),
# Output layer with sigmoid activation
tf.keras.layers.Dense(1, activation="sigmoid")
])