This is a code to calculate ARPES spectra for slabs with an accumulation or a depletion surface layer. The calculation proceeds in two steps:
- The Poisson and the Schrödinger equations are solved self-consistently
to obtain eigen-pairs {
En,ψn(z)}. - ARPES spectra are then calculated using a Fourier transform of
ψn(z), followed by a convolution with normal distributions to account for instrumental broadening.
1D finite elements (esf library)
are used to discretize the Poisson and the Schrödinger equations.
The Intel MKL library is used to solve linear systems, generalized eigenvalue
system, compute Fourier transforms and convolution. The mathematical details
can be found in this PDF file.
The results are exported into Matlab/Octave MAT-files and Gnuplot binary matrix files.
All images below are presented for exposition only, no attempt has been made here to fit any experimental data.
Depletion layer (no bound states):
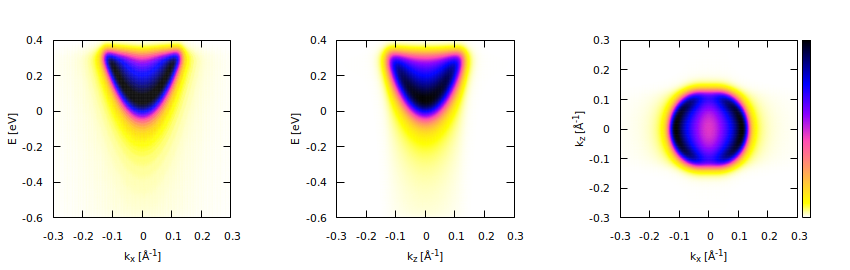
Accumulation layer with one bound state:
Accumulation layer with two bound states:
Set MKLROOT environment variable to point to the MKL installation directory,
and be sure that your CMake version is >= 3.13. Then:
git clone --recursive https://github.com/eugnsp/surface_arpes.git
cd surface_arpes
mkdir build && cd build
cmake -DCMAKE_BUILD_TYPE=RELEASE .. && maketo build the tool.
C++17 compiler is required. Tested with GCC 8.3.0 and Clang 7.0.
./arpes [file]
./arpes ../example/accum1.txt
./arpes < ../example/accum1.txtwhere file is the text file with simulation parameters (see examples in
the example directory). The standard input is used to read parameters
if no file is specified.
You can run arpes via a shell script
echo '#!./arpes' > accum1.sh
cat ../example/accum1.txt >> accum1.sh
chmod 755 accum1.sh
./accum1.shThe following output files are produced:
-
poisson_cl.matandpoisson_q.matThe Matlab files that contain the following variables:
vertices– mesh pointszi[nm],ec–Ec(zi)at mesh points [eV],f– the Fermi level [eV],n– the total charge densityn(zi+1/2)at edge mid-points [eV].
poisson_cl.matcorresponds to the solution obtained using the quasi-classical Thomas–Fermi approximation,poisson_q.matcorresponds to the solution obtained using the Schrödinger equation. The former one is used as an initial guess for the Poisson–Schrödinger iterative solver. -
schrod.matThe Matlab file that contains the solution of the Scrödinger equation obtained at the last iteration:
en– the eigen-energiesEn,psi– the eigen-functionsψn(zi).
-
arpes.matThe Matlab file that contains the calculation parameters and ARPES spectra. The variables are:
arpes_e_kz– the(E, kz)spectrum,arpes_kx_e– the(kx, E)spectrum,arpes_kx_kz– the(kx, kz)spectrum,e_min,e_max– the energy rangeEmin ≤ E ≤ Emax[eV],kx_max– the momentum range-kx max ≤ kx ≤ kx max[Å-1],kz_max– the momentum range-kz max ≤ kz ≤ kz max[Å-1],mfp– electron mean-free pathλ[nm],sigma_e_inst– the instrumental broadeningδAE[eV],sigma_kx_inst– the instrumental broadeningδAk[Å-1],gamma_disorder– the disorder broadeningδDE[eV].
-
arpes_e_kz.dat,arpes_kx_e.dat,arpes_kx_kz.datThe binary files that contain ARPES spectra for visualization using Gnuplot, see shell scripts in the
plotdirectory. The figures above were generated using theplot/plot_all.shshell script.
- V.N.Strocov. Photoemission response of 2D states.
J. Electron. Spectrosc. 229, 100 (2018), arXiv preprint (2018). - S.Moser et al. How to extract the surface potential profile
from the ARPES signature of a 2DEG.
J. Electron. Spectrosc. 225, 16 (2018). - A.Trellakis et al. Iteration scheme for the solution of the
two-dimensional Schrödinger–Poisson equations in quantum
structures.
J. Appl. Phys. 81, 7880 (1997).
This code is distributed under GNU General Public License v3.0.