Tiered Vectors: Efficient Dynamic Arrays for Rank-Based Sequences [243ko pdf]
by Michael T. Goodrich and John G. Kloss II
WADS 1999. Lecture Notes in Computer Science, vol 1663 https://doi.org/10.1007/3-540-48447-7\_21

This library provides an implementation of variable sized arrays, which are also called resizable arrays, dynamic arrays or even "vectors" in C++ and "ArrayList" in Java. Just like an array, accessing any element by its index is constant time, but one can also efficiently insert and delete at any location (with the array resizing automatically to meet the need).

Online Documentation

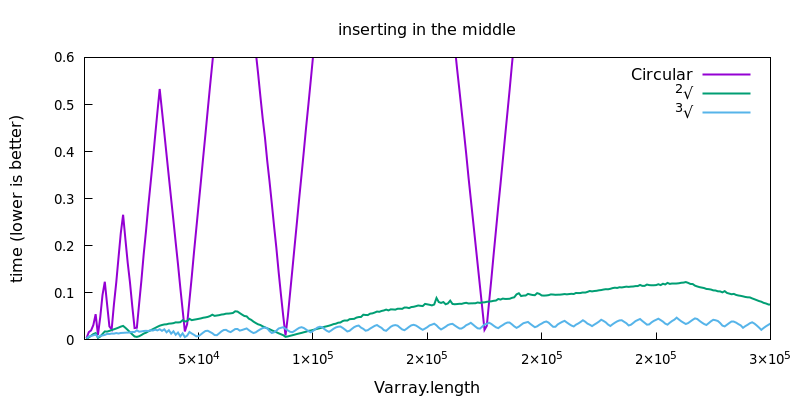
Following the above paper, the family of tiered vectors yields a nice compromise between random access and resizing:

Module Circular	get, set	{push,pop}_{back,front}	insert_at, pop_at	Memory overhead
Circular	O(1)	O(1) amortized	O(N)	O(N)
Root(Circular)	O(1)	O(1) amortized	O(√N)	O(√N)
Rootk-1(Circular)	O(k)	O(k) amortized	O(k2 × k√N)	O(Nk-1 / k)

In other words, each instantiation of the Root functor leads to slower random access into the array, but it also makes insertion and deletion faster!

You can expect the following constant factors on random access:

	Array	Circular	Root	Root2	Root3	Root4	Root5
get	1x	3x	8x	17x	27x	31x	33x
set	1x	2x	4x	8x	12x	14x	15x

The memory usage is competitive:

• push_front, push_back and their respective pop, are amortized constant time, since they frequently need to allocate small chunks of O(^k√N) up to O(k ^k√N) memory as the varray grows or shrinks.
• The growth strategy is incremental: the worst case slowdown following a resize is also O(k ^k√N) which is unobtrusive for k>1. There is no "stop the world while every elements is moved to a larger array".
• The amount of memory used for bookkeeping and allocated in anticipation of a growth is pretty tight. In particular for k=2, the O(√N) memory overhead is optimal if random access and push_back are to be O(1).

If you only care about fast random access and resizing at the right end with {push,pop}_back, then the pre-existing libraries provide smaller constant factors : (in alphabetical order) BatDynArray from Batteries, CCVector from Containers, RES as a standalone library or even vector as a single module.