Haworth projection
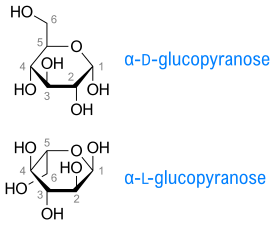
In chemistry, a Haworth projection is a common way of writing a structural formula to represent the cyclic structure of monosaccharides with a simple three-dimensional perspective. Haworth projection approximate the shapes of the actual molecules better for furanoses—which are in reality nearly planar—than for pyranoses that exist in solution in the chair conformation.[1] Organic chemistry and especially biochemistry are the areas of chemistry that use the Haworth projection the most.
The Haworth projection was named after the British chemist Sir Norman Haworth.[2]
A Haworth projection has the following characteristics:[3]
- Carbon is the implicit type of atom. In the example on the right, the atoms numbered from 1 to 6 are all carbon atoms. Carbon 1 is known as the anomeric carbon.
- Hydrogen atoms on carbon are implicit. In the example, atoms 1 to 6 have extra hydrogen atoms not depicted.
- A thicker line indicates atoms that are closer to the observer. In the example on the right, atoms 2 and 3 (and their corresponding OH groups) are the closest to the observer. Atoms 1 and 4 are further from the observer. Atom 5 and the other atoms are the furthest.
- The groups below the plane of the ring in Haworth projections correspond to those on the right-hand side of a Fischer projection. This rule does not apply to the groups on the two ring carbons bonded to the endocyclic oxygen atom combined with hydrogen.
See also
[edit]References
[edit]- ^ Campbell, Mary K. (2012). "16". Biochemistry. Shawn O. Farrell (7th ed.). Belmont, CA: Brooks/Cole, Cengage Learning. p. 456. ISBN 978-0-8400-6858-3. OCLC 651905707.
- ^ Haworth, Walter Norman (1929). The Constitution of Sugars. London, England: Edward Arnold & Co.
- ^ IUPAC, Compendium of Chemical Terminology, 2nd ed. (the "Gold Book") (1997). Online corrected version: (2006–) "Haworth representation". doi:10.1351/goldbook.H02749
 | This stereochemistry article is a stub. You can help Wikipedia by expanding it. |