Introduction
Many studies have observed the internal reflections of radio waves within the ice sheets of Greenland and Antarctica. They appear, usually as multiple layers, on photographic records of the radio echo returned to an aircraft or surface vehicle which is equipped to transmit and receive pulsed r.f. signals. The technique is described by Reference Bailey, Bailey, Evans and Robin.Bailey and others (1964), Reference Robin, Robin, Evans and BaileyRobin and others (1969), Reference Robin, Robir, Swithinbank and Smith.Robin and others (1970), Reference Gudmandsen and GudmandsenGudmandsen (1970), Reference HarrisonHarrison (1973), and Reference GudmandsenGudmandsen (1975). Individual echoes tend to follow bedrock relief and can often be traced for up to 100 km along a Might line in Antarctica, and for hundreds of kilometres in Greenland. Reference HarrisonHarrison (1973) has discussed in detail whether these reflections are due to a few widely spaced layers of markedly different properties or due to the vectorial sum, within the pulse length, of reflections from many less distinct and more closely spaced internal layers. He concluded on statistical grounds that the latter description was more likely, for layers at spacings less than about half a pulse length cannot be resolved by the echo sounder, and a continuous echo on the record does not necessarily represent a single layer. Despite this uncertainty in the vertical widths of the layers, it is clear that the stratifications are indeed sedimentary since their electrical variation is incorporated very uniformly over wide expanses of the ice sheets presumably at the time of deposition. Indeed Reference Robin, Robin, Evans and BaileyRobin and others (1969) confirmed that, given a steady-state mode! for the dynamics of the Greenland ice sheet, a prominent echo horizon which was traced for 45 km south from Camp Century, could be dated as the surface layer in A.D. 975±100.
Reflection coefficients—theory
For our immediate discussion we consider two very simple models of an ice sheet which would produce an echo:
-
(i) ice of intrinsic admittance r overlying, at a single boundary, ice of admittancer + Δr.
-
(ii) ice of admittance r containing within itself one layer of thickness l with admittance r + Δr.
At normal incidence and for Δ r ≪ the reflection coefficient R for a wavelength in the ice of λm is: in model (i)

and in model (ii)


where R s is the single boundary reflection coefficient. In all previous studies the admittance mismatch between layers has been assumed to be simply due to permittivity changes

but if this mismatch is due to the loss tangent varying from tan б to tan б + Δ (tan б) then

It is possible to extend the arguments of Reference HarrisonHarrison (1973) which involve the more complicated multilayer geometries by the substitution of Δ (tan б) for ε/ε in the reflection-coefficient equations. However, since our discussions will be primarily concerned with the relative importance of variations in the loss tangent and permittivity we shall only study the first model in order to calculate R s, for, in the second model and other cases, the relevant reflection coefficients may be obtained by multiplying R s by geometrical factors.
In this article, we summarize the values of internal reflection coefficients that are calculated from theory using some detailed observations of the ice stratigraphy that have been carried out on cores drilled from polar ice sheets. We then present the radio echo-sounding evidence on the magnitude of the reflection coefficients, which, for deeper echoes in polar ice sheets, are higher than can be satisfactorily explained by previous theories. After discussing possible causes of variations of tan б in polar ice, we conclude by giving the laboratory and field evidence on the values of the conductivity of polar ice and show how plausible it is that many of the deeper echoes are caused by variations in the loss tangent of the ice.
According to Reference Robin, Robin, Evans and BaileyRobin and others (1969) and Reference HarrisonHarrison (1973) the sedimentary variations in the permittivity may be due to:
-
seasonal fluctuations in the density of deposited ice,
-
inclusion of “foreign” material such as
-
(a) dust or
-
(b) volcanic ash,
-
-
(c) orientational differences of the c-axes in the ice-crystal matrix.
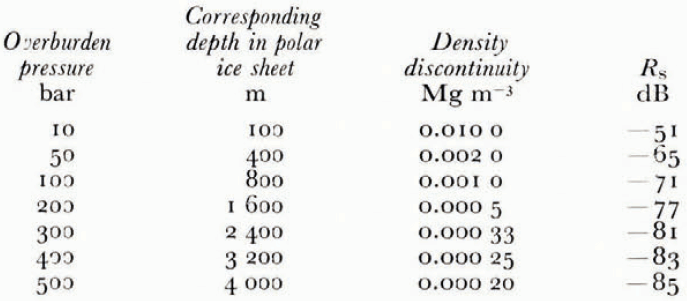
In Table I we give the reflection coefficient Rs for a set of discontinuous density changes across a single boundary. Any density change can correspond to a difference in density between bubble-free ice and bubbly ice at a given over-burden pressure. Each density change is associated with the equivalent depth in Table I. This table also indicates the greatest value of the reflection coefficient that one may reasonably expect from a single change of ice density with depth in a polar ice sheet.
Table I Reflection Coefficient r s for the Boundary Between Bubble-Free and Bubbly Ice where the Bubble Pressure Equals the Overburden Pressure. THE Atmospheric Pressure is Taxen as 700 mbar to Allow for a Surface Elevation of the the Sheet of Rouchly 3000 m
Dirt and ash bands in the core drilled from “Byrd” station, Antarctica were found between 1 300 m and 1 700 m depth (Reference Gow, Gow, Ueda and GarfieldGow and others, 1968). The volcanic ash bands were about 0.5 mm thick but were always overlain by a layer of refrozen melt water which could attain a thickness of 10 mm. Reference HarrisonHarrison (1973), in considering the effect on the permittivity of mixed ice and rock particles has calculated that the reflection coefficient at 35 MHz from a single ash band 0.5 mm thick is —106 dB. In the “Byrd” core, Reference Gow and WilliamsonGow and Williamson (1971) observed occasional “very fine” dust layers with a typical dust concentration of 0.04 kg m−3. The resultant permittivity derived from this mixture is only 2 × 10 −5 higher than the value for dust-free ice, so the value of Rs for the boundary between clear and dusty ice would be —116 dB.
It is not known whether there is an anisotropy in the radio-frequency permittivity of single crystals of ice. Laboratory experiments below 1 MHz are neither sufficiently precise nor sufficiently repeatable to reveal any anisotropy after extrapolation of the dielectric parameters to higher frequencies. Differences in orientation between the ice crystals which make up the
ice sheet might nevertheless account for differences in permittivity between layers, and supporting evidence comes from observations of the azimuthal dependence of the polarization of radio waves reflected from glacier beds (Harrison, 1973; Reference CloughClough, unpublished). Quantitative assessment of these results is difficult, however.
Reflection coefficients—observations
To determine the reflection coefficient for an internally reflected echo it is necessary to measure the returned echo strength at the receiver. This signal is subject to attenuation; the most important effects are due to the geometrical spreading of the radar pulse and to absorption by the dielectric conductivity of the ice. The absorption losses have been calculated assuming that the conductivity values which lead to the loss tangents for polar ice at 35 MHz given in Tables II and III are applicable in every situation (and we return to this assumption later), and by estimating the temperature profile through which the signal is attenuated.
The reflection coefficients calculated by this method are found to be around —70 dB. In particular, using a 35 MHz radar, values between —72 and —80 dB were deduced for the A.D. 975 layer in Greenland (Reference Robin, Robin, Evans and BaileyRobin and others, 1969), values between —60 dB and —83 dB for layers observed between 2 000 and 3 000 m depth in east Antarctica between Vostok and
Table II. The Loss Tangent at 35 mhz for Polar Ice Deduced from the Measurements of Westphal and Reference Paren, Whalley, WhaLiey, Jones and Gold.Paren (1973). The Reflection Coefficient r s is Calculated for the Boundary Between this Ice and Ill Whose Loss Tangents are tan б ± Δ (tan б) Δ (tan б)/ tan б = 0.2, 0.5 and 0.8 Respectively

Table III. The Loss Tangent at 35 mhz for Pure Ice, Based on the Audio-Frequency Dispersion, and for Polar Ice Deduced from the Measurements of Westphal and of Reference Paren, Whalley, WhaLiey, Jones and Gold.Paren (1973). The Reflection Coefficient rs is Calculated for the Boundary Between Pure Ice and Polar Ice

McMurdo (Reference HarrisonHarrison, 1973), and a value around —69 dB at “Byrd” station in west Antarctica for a prominent internal layer at a depth of 1 300 m (Reference Robin, Robir, Swithinbank and Smith.Robin and others, 1970). Reference GudmandsenGudmandsen (1975) deduced reflection coefficients of between —70 dB and —75 dB for layers observed at Crête in central Greenland at depths of 1 900 m and between 2 300 m and 2 500 m using a 60 MHz sounder. These observed reflection coefficients are far higher than those calculated from dust, and dirt and ash discontinuities.
Loss tangents
Estimates of the mean loss tangents for vertical sections of an ice sheet are derived in directly from the observed strengths of echo returns during radio-echo sounding. The conductivity of the ice derived from the field data is in general agreement with the high-frequency conductivity of the Debye dispersion observed in laboratory experiments on deep ice cores drilled from Greenland, Arctic Canada and Antarctica, and investigated at the same temperature. The laboratory experiments are due to Westphal (reported in Reference EvansEvans, 1965), Reference Paren, Whalley, WhaLiey, Jones and Gold.Paren (1973), Reference MaenoMaeno (1974) and Reference Fitzgerald and ParenFitzgerald and Paren (1975), and these experiments have been reviewed by Reference Glen and ParenGlen and Paren (1975). It is found that between 10 kHz and 500 MHz the frequency dependence of the conductivity is small, and the conductivities of samples drilled from the same or different sites are similar but not absolutely identical. The similarity is puzzling, for the behaviour is not the same as is observed in “pure” ice grown in the laboratory by the controlled slow freezing of pure water. The conductivity measurements by Westphal at 150 MHz on an ice sample from TUTO, Greenland, and another from the Ward Hunt Ice Shelf, Canada, were entirely consistent with the mean behaviour of ten samples from Camp Century and Site 2, Greenland, investigated at 100 kHz by Reference Paren, Whalley, WhaLiey, Jones and Gold.Paren (1973); this self-consistent relationship between conductivity and temperature has been used to deduce the loss tangent at intermediate frequencies, and the value deduced for 35 MHz is given in Tables II and III. Why the behaviour of polar ice should be so different from “pure” ice is still an open question. Reference Fitzgerald and ParenFitzgerald and Paren (1975) have shown that, when melted polar ice (drilled from “Byrd” station, Antarctica) is refrozen slowly in the laboratory, the behaviour reverts to that of “pure” ice. This leads to the suggestion that the electrical behaviour depends on the initial growth conditions, and it is known from the studies of Reference Evrard, Whallry, Whalley, Jones and Gold.Evrard (1973) and Reference Boned, Barbier, Whalley, Whalley, Jones and Gold.Boned and Barbier (1973) that ice that is formed by the nucleation of supercooled water droplets at low tempera ture has a dielectric response that “ages” with time to values similar to that of polar ice and is thus distinctly different from that of ice made by the slow freezing of water.
If impurities are added to the water from which ice is grown slowly, the conductivity is raised above the “pure” ice values, the differences increasing with increasing impurity concentration (sec Reference Camplin, Glen, Whalley, Whalley, jones and Gold.Camplin and Glen (1973) for the effect of the addition of HF). Thus, although the initial nucleation of the snow in the high atmosphere might explain the dielectric properties of the purest polar ice, the impurity concentration should also be considered. It may be realistic to associate the experimentally observed small variations in conductivity between adjacent samples of ice taken from the same ice core with a change in impurity concentration, but the level of impurity is very low indeed and difficult to measure directly. However, observations of similar electrical behaviour from many sites where the impurity levels although very low, are different, tends to lead one to the conclusion that the impurity level may be so low as to be unimportant.
Nevertheless, if both initial growth conditions and impurity concentrations are important in polar ice, we can make use of the model of Reference Paren and WalkerParen and Walker (1971). They considered the distribution of impurities in the ice, and suggested that impurities were incorporated into the crystal lattice up to a certain “solubility limit”, beyond which further impurities collected at the grain boundaries in which location their contribution to the dielectric behaviour was much reduced. It may be that the nucleation and firnification of polar ice, in the absence of
melting, provides mechanisms by which impurities are effectively distributed throughout the crystal lattice, whereas during melting and refreezing the impurities may tend to remain in the water. Thus the refrozen ice of Reference Fitzgerald and ParenFitzgerald and Paren (1975) may have contained less impurities in the crystal lattice than the original material, but more at the crystal boundaries. We can thus reconcile the different ideas and observations, since the varying but low levels of impurity in polar ice could still cause variations of tan б between layers, especially if the impurity levels fluctuate around or below the “solubility limit”.
The absolute value of the limit of solubility in ice and its variation with different impurities has not been determined experimentally except for the acids HF and HC1, For HF, the ratio of the number of acid molecules to water molecules at the solubility limit at —10± C is 4 × 10−5 and the corresponding mole fraction for HC1 is 1.4 × 10−7. We expect that other inorganic salts such as the sea salts would have a still lower limit of solubility (Reference Glen and ParenParen and Walker, 1971). During radio-echo sounding in central Antarctica the dielectric absorption has been found to be about 20% lower than would be found elsewhere at the same temperature, and the very low level of impurity present could be the cause. For instance at the South Pole the concentration of chloride ions is 1.5 × 10−8 mole fraction and ammonium ions are found at less than 10−9 mole fraction. These results suggest a value of the order of 10−8 to 10−7 mole fraction for the solubility limit in ice of atmospheric- and sea-salt impurities. It may however be wrong to think in terms of a sharply defined limit, rather than a rapid falling off in the gradient of (tan б — tan б (“pure”)) with impurity content, once the impurities reach some level which will be a function of the types of impurity that are present.
General discussion
In Table II we have calculated the reflection coefficients R s at 35 MHz between polar ice and ice for which the loss tangent is some fixed proportion of this. The values chosen for Δ(tan б)/tan б are 0.2, 0.5 and 0.8. This model was chosen since measured differences in behaviour between samples from the same site are usually contained in the value of the loss tangent at a given temperature rather than in the activation energy, which determines the temperature dependence.
In Table III there is a similar calculation for polar ice overlying “pure” ice, and such reflection coefficients also apply to the boundary between polar ice and ice which has been melted and subsequently refrozen in situ. Such a boundary is found above dirt layers as mentioned previously.
Comparison of Table I with Tables II and III shows an important difference between internal reflections due to variations of density and of loss tangent. Irrespective of the type of layering, internal reflections due to density effects will weaken with increasing depth in the ice. In contrast, internal reflections due to variations in the loss tangent will become stronger towards the bottom of the polar ice sheet, since the temperature increases with depth.
Figure 1 shows the returned echo strength at the receiver for a location in central Antarctica (lat. 77° S., long. 124° E.). The data used come from the A-scope display of Reference HarrisonHarrison (1973). Also shown on this figure are the expected echo strengths at the receiver after attenuation through the ice from single boundaries with the reflection coefficients indicated on Tables I and II choosing Δ(tan б) = 0.5 tan б only. The calculated lines showing tan б and density changes have an arbitrary intersection with the 0 m datum. However, their gradients are not arbitrary; the important comparison to be made is between the relative gradients of the observed and calculated returned signal strengths rather than the absolute values, which depend on the type of layering. There is a small additional effect, however, not included in the calculations, due to plastic deformation of ice, which leads to a single layer thinning as it becomes more deeply buried in a way that keeps its width proportional to the height of the layer above bedrock. This does not change the argument significantly, unless there have been major changes in the depositiuii rates of ice and impurities within Lhe time scale of the ice section investigated. Figure I shows that the change in strength of internal reflections with depth follows the trend of density variations to a depth of about i 500 m. Beyond that depth, the observed trend is much better explained by reflections resulting from variations of the loss tangent.
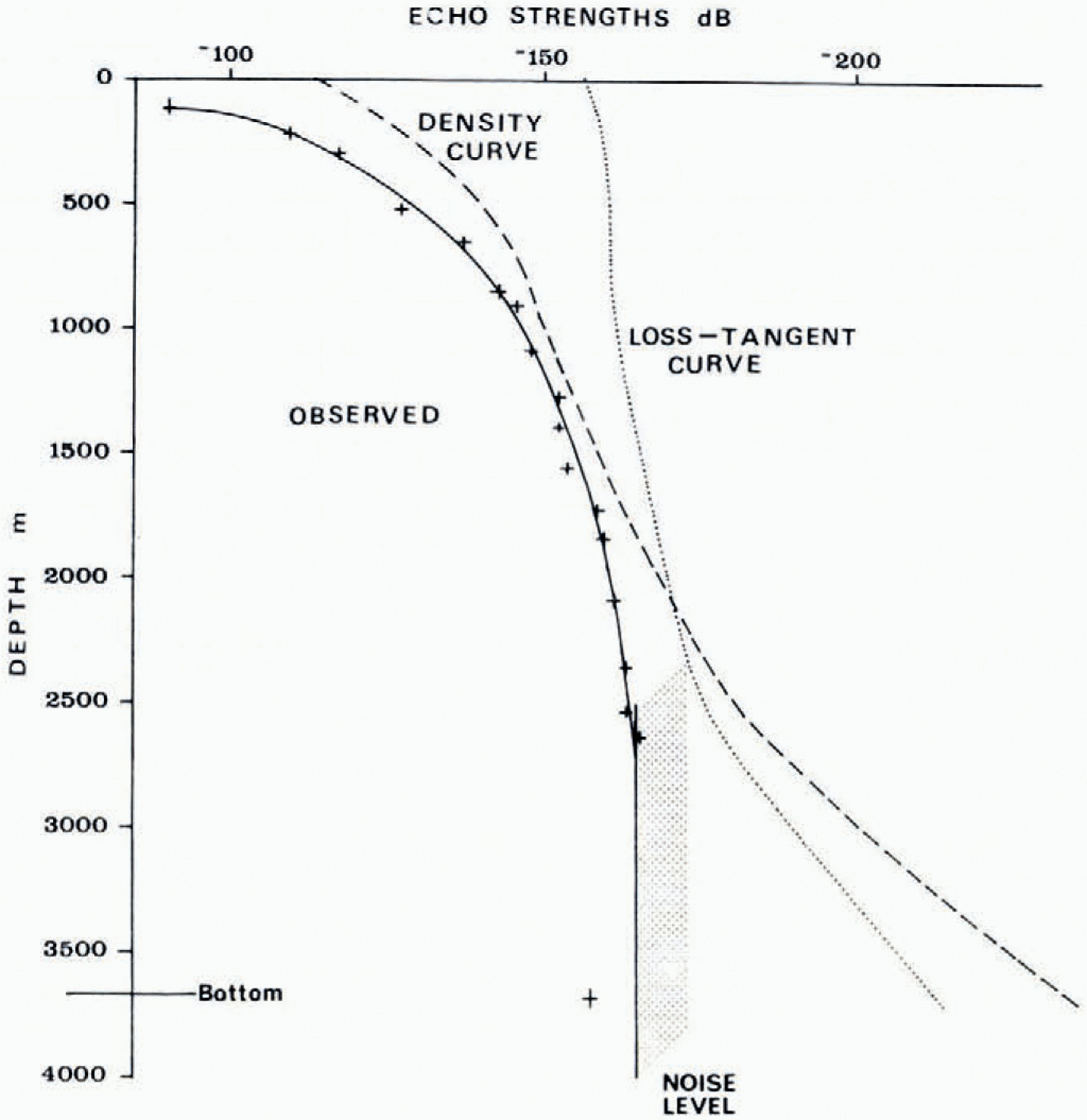
Fig. 1. Variation in the strength of internal reflections in central Antarctica. The gradients of the theoretical curves depicting changes in density and loss tangent should be compared with the field observations. The loss-tangent curve is computed for Δ(tan б)/tan б = 0.5 at 60 MHz.
On the assumption that the reflection coefficient from internal layers docs not change over a 1 km depth range, Reference HarrisonHarrison (1973) has derived mean attenuation coefficients and reflection coefficients for the ice between 2 000 m and 3 000 m depth in central Antarctica. This was achieved by fitting a straight line to the local power maxima on the A-scope display. His attenuation values were from 3 to 8 dB km−1 corresponding to ice temperatures of —40 to —50° C from Tables II and III. This is indeed the surface temperature in this area, but temperatures at 2 000-3 000 m depth are expected to be between —10 and —40 ° C averaging perhaps —25° C, and we would have expected attenuations higher by about 4 dB km−1. This discrepancy in values would be removed entirely if the reflection coefficient at the 2 000 m depth level were 8 dB lower than at 3 000 m. Indeed, if the ice at 3 000 m depth is 15 to 20° C warmer than at 2 000 m depth, then we can see from Tables II and III that the reflection coefficient should increase by about 8 dB over this range due to temperature changes alone.
Thus we obtain reasonable agreement between the measured and expected attenuations in deep Antarctic ice once the temperature profile has been estimated and the relevant reflection coefficients calculated from Table II or III.
Conclusions
The observations support the view that deep internal reflections are due to changes in loss tangent between layers. Two possible causes of the change in loss tangent between layers have been suggested. The first is varying impurity concentrations between layers. There is some evidence that such variations do occur, but there is no experimental evidence showing a direct relationship between these low impurity levels and the values of the loss tangent in polar ice. However, variations with time in the impurities deposited from the atmosphere in the snow of polar ice sheets would provide an acceptable explanation of the spatial and temporal variations necessary to form reflecting layers that extend over very large distances. The second possible cause is the difference between loss tangents of “polar” ice and “pure” ice, the latter having been formed by melting polar ice above dust layers or from other causes. Again, there are no direct measurements of the dielectric absorption in such ice layers from an ice core. Also it is less likely that the temporal and spatial occurrences of such ice layers would fit the observed distribution of internal reflections, especially in central Antarctica where reflections are prominent but surface melting is rare.
Whatever their cause, it seems clear that variations in the loss tangent provide a better explanation of the very deep internal reflections in polar ice sheets than do variations in the permittivity. While our discussions of permittivity have concentrated on the effects of density variations, we have also pointed out that dust layers in the ice could not account for the observed reflections. We have not discussed possible effects of anisotropy in different layers because of lack of measurements of permittivity along different crystal axes. We should emphasize however, that even if there is a significant effect, it is unlikely to vary much with temperature. Consequently the gradient of a curve associated with an anisotropic boundary in Figure 1 will be much closer to the density curve than the tan б curve, which in turn indicates that anisotropic layering is unlikely to provide an explanation for the very deep echoes. On the other hand, it appears likely that permittivity changes due to density fluctuations do provide a reasonable explanation of the layering observed above a depth of i 500 m in central Antarctica.
Acknowledgement
We thank Dr S. Evans for his continued encouragement in this work and Dr D. R. Homer for many helpful discussions. This work was partially supported by the Natural Environment Research Council.





