2.1.

Observations

In this work, we used the calibration observations taken for Spitzer Program ID (PID) 1336 and PID 1367. Specifically, we observed a set of 10 stars with varying exposure times, in both subarray and in full array, and in staring and dithering modes. Almost always, staring-mode observations were taken on the same pixel (the sweet spot), as that pixel was the best characterized pixel on the array. Table 2 lists the stars. We searched the archive for additional data usable for this analysis but did not find anything suitable, combining nonvariable stars with observations in all available modes and having a sufficient number of images to achieve statistical significance.

Table 2

The calibration star sample.

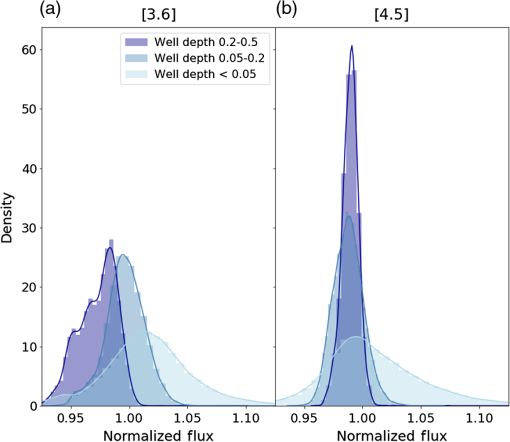
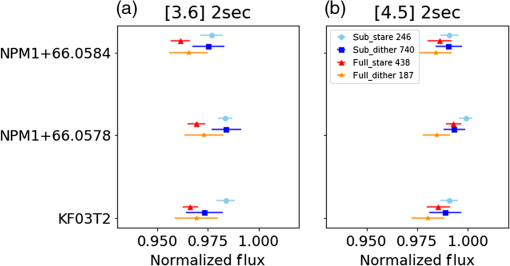
Figure 1 shows a visualization of this dataset. We plot the exposure time(s) versus aperture flux for just the [4.5] channel. Similar observations were made for [3.6]. All stars were observed with multiple exposure times. Not all of the 10 stars could be observed at all exposure times due to SNR and saturation concerns. This plot illustrates how the range of stellar brightnesses and frame times in the sample filled the available phase space.

Fig. 1

Description of the dataset used in this work for the [4.5] channel, showing (a) the aperture flux as a function of the exposure time and (b) aperture flux as a function of well depth. The [3.6] channel has a similar observation set but for brevity is not shown. Points are color coded by star names, and symbol shapes denote full (filled circles) or subarray (crosses). Each data point represents one observation, and data are not binned, but there are overlapping data points.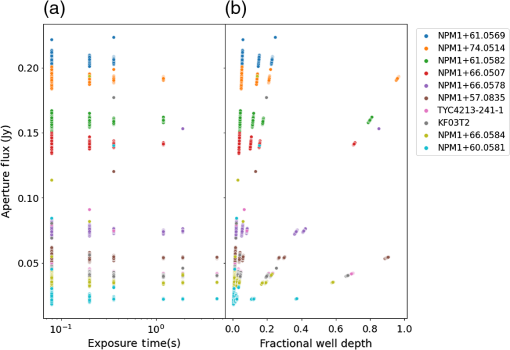

We considered how close to saturation (well depth) a star is as a means of interpreting our results. Looking at our sample as a whole, the range of possible well depths is not well sampled; having a median fractional well depth of 0.04 and 0.02 at [3.6] and [4.5], where a fractional well depth of 1.0 indicates saturation. Figure 1(b) shows well depths of the sample. The median well depths of our sample correspond to an SNR of 39 and 24 at [3.6] and [4.5], respectively. This dataset was not designed with well depth in mind and was instead designed to find stars that would sample the available exposure time parameter space.

Although available, we reject the 0.02-s photometry because of its large scatter. We have also rejected any data where the well depth is greater than the listed saturation limit in the IRAC Instrument Handbook.⁴ The saturation limit results in the rejection of around 250 photometry points at [4.5]. All observations used in this work have SNRs of six or greater.

For a subset of three stars, we made a larger number of observations in all possible modes with 2-s frame times in both channels. This allowed us to build up statistically meaningful samples where we hold the frame time constant while varying the other observing parameters. The three stars are NPM1+66.0584, NPM1+66.0578, and KF03T2.

The 2-s frame time is the closest set of IRAC frame times available for holding exposure time constant between the full and subarray. Unfortunately, the 2-s subarray and 2-s full-array frame times do not actually correspond to the same exposure times: 1.92 and 1.2 s, respectively. Similarly, frame times of 0.4 s in full and subarray also have different exposure times, so frame time was not a good alternative. This difference in the exposure times for the same frame time comes from a different number of Fowler numbers ($N$), wait ticks, and readout times for the different modes as listed in the IRAC Instrument Handbook. Briefly, Fowler sampling is a way of observing by taking $N$ nondestructive reads at the beginning of the observation and another $N$ nondestructive reads at the end of the observation, the difference of which is the flux measured per pixel.

All of the stars chosen for this work were vetted as potential calibration stars for IRAC. Seven of the 10 stars are published as primary or secondary calibrators for IRAC known to not exhibit flux variability in the IRAC bands.⁵ The three stars not included in that reference are NPM1+74.0514, NPM1+57.0835, and NPM1+66.0584. Specifically, NPM1+66.0584 is one of the three stars in the subset taken with more observations in 2-s frame times. We cannot use this dataset to determine both if the stars are time variable, and if they vary as a function of the other parameters studied herein. While vetted, because these have not specifically been published as calibration stars, we experimented with removing these three stars from our sample. All plots look similar (albeit with larger scatter due to fewer data points), and conclusions remain the same if we remove those stars from the sample. We therefore choose to keep these in the sample for the remainder of this work.

Each of the [3.6] and [4.5] datasets includes about 80,000 total individual observations. Specifically, for each channel, we have roughly 65,000 subarray and 15,000 full array observations.

2.2.

Photometry

We briefly describe our pipeline here, emphasizing where it differs from previous work. For an overview of the Spitzer/IRAC absolute photometric calibration, see Refs. 5 and 6. Specifics of the photometry pipeline used here are included in Ref. 7. We used the basic calibrated data (BCD) FITS files (suffix bcd.fits) from the Spitzer Heritage Archive (SHA). These BCD files have had a dark correction, flat-field correction, linearity correction, and conversion to flux units already applied.

One somewhat new aspect of this work is that we apply a different dark correction to staring-mode data than we do to dithered observations. Staring-mode data are processed in the standard pipeline in the same manner as dithered data, including using a dark image that was made by dithering. The delay time between frames affects the bias level in the frame (including in the dark); this is known as the “first-frame effect.” Therefore, dithered observations will have different bias levels and patterns than staring-mode observations since staring-mode observations have shorter delay times between consecutive frames, although that pattern is constant if the delay time is constant. This effect adds both noise and systematics to the photometry. For this reason, dithered darks are inappropriate for staring-mode science frames when precision photometry is required.

We used PID 1345 to make our own staring-mode dark suite for all subarray frame times. We began by removing the dithered dark correction from the PID 1345 data. Because the dark correction is not the last correction made to the BCD files, care was taken to first back out the other corrections, apply the staring-mode dark, then reapply the other pipeline corrections. We then created a median image for each exposure time (0.02, 0.1, 0.4, 2.0 s) and used this median frame as the staring-mode dark. Applying this new staring-mode dark to the staring-mode data has a measurable impact on derived fluxes. We recommend that anyone doing precision photometry with staring-mode data uses a staring-mode dark instead of the pipeline-provided, dithered dark. While the IRAC pipeline will not include these starting-mode darks, code is available for users to change which darks are used in a BCD frame on the contributed-code section of the Spitzer IRAC website.⁸

To measure flux, we use our appropriately dark-corrected BCD exposures and make the following corrections in order. We first convert images into units of electrons to enable a statistical calculation of uncertainties. Second, we use a center-of-light method to find stellar centroids.⁹ Third, we do aperture photometry with a three-pixel radius aperture and (3-7) pixel background annulus. The small aperture size is chosen to reduce noise and the number of cosmic rays in the aperture. Fourth, we make a correction for pixel-phase using pixel_phase_correct_gauss.pro.¹⁰ The pixel-phase correction accounts for gain changes as a function of the position within a pixel, coupled with the undersampling of a point source by IRAC. Fifth, we make a correction for array location. The array location-dependent correction takes into account the variation in system response of the instrument across the field of view, which is primarily due to the change in the angle of incidence of light through the bandpass filter as a function of position on the array. Lastly, we discard the first frame of every subarray FITS file and of every full array AOR. These frames are affected by the first-frame effect discussed above and are likely to have measured fluxes that differ from those of subsequent images. We do not apply an aperture correction since the same aperture is used for all photometry regardless of observing mode.

To compare photometry for all stars on the same plots, we normalize the stars to the same absolute level by dividing all photometry by the median stellar fluxes. The distributions of fluxes per star are somewhat skewed, so a mean does not capture the peak of the distribution. Having skewed distributions causes the mean levels in the subsequent plots to differ from unity.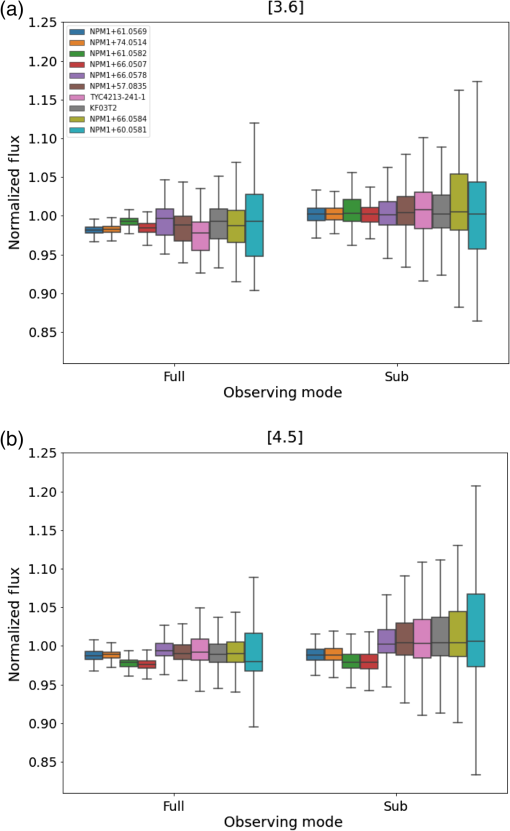

3.1.

Array Mode—Full versus Subarray

Figure 2 shows the [3.6] and [4.5] photometry (top and bottom respectively) of the stars in Table 2 as a function of array mode, revealing that the measured fluxes appear on average to be lower for the full-array observations than the subarray observations of the same stars. We attempt to confirm this statistically using an Anderson two-sample test, per star, to see if the distributions for full array and subarray are drawn from the same population. This statistical method considers the vertical distance between the two cumulative distributions. For all 10 stars, we can say that the full array and subarray data are not drawn from the same distribution at the 25% significance level (maximum possible significance). Thus, the difference between the fluxes measured in full array and subarray modes is statistically significant. Using all 10 stars, the median difference between the full and subarray flux measurements is 1.6% at [3.6] and 1.0% at [4.5].

3.2.

Frame Time

Figure 3 shows the distributions of normalized calibrator star fluxes as a function of frame time. [4.5] includes more data on the 6-s full-array frame time, so the bottom plot includes that frame time whereas the [3.6] plot does not. The median normalized flux of all the stars changes as a function of frame time such that the measured fluxes are larger at lower frame times. This is most strongly evident in [3.6]. Figure 4 shows a measure of the strength of this effect as the median difference between the 2-s and 0.4-s frame time fluxes for all the stars, per channel, per observing mode.

Fig. 3

Box plot of the distributions of normalized fluxes of all the stars as a function of exposure time at (a) [3.6] and (b) [4.5]. Frame time labels also indicate full or subarray. Color coding is the same as for Fig. 2. On average, fluxes measured at longer frame times are lower than those measured at shorter frame times.

Fig. 4

Exposure-time effect for both channels divided into bright and faint stars to look for an effect with star brightness. [4.5] is shown in the top half of the diagram, while [3.6] plotted in the lower half. Blue circles show the median difference for all the stars observed in the full array between the 2- and 0.4-s frame time normalized fluxes, including one sigma error bars. Blue right and left triangles show the median values for the bright and faint populations of stars. The same quantities are plotted for subarray data in red.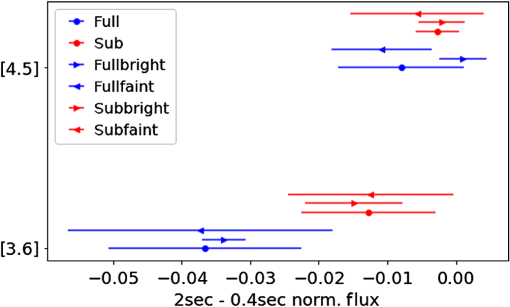

As in Sec. 3.1, we used the Anderson two-sample test to compare the full-array 0.4-s observations with the full-array 2-s observations. For both channels, we find the difference between the normalized flux distributions at the two frame times to be statistically significant. The same is true for fluxes from the subarray in 0.4- and 2-s frame time observations.

We tested whether the trend seen in flux as a function of exposure time depends on stellar brightness such that the brighter or the fainter stars would be more or less likely to show this effect. We do this by calculating the difference between the 2- and 0.4-s normalized fluxes. A difference between the fluxes implies that different fluxes are measured using different exposure times. Because we know there is an effect with array mode, we divide the sample into full and subarray data. Finally, looking for a trend in the stellar brightness, we divided the sample into bright and faint stars and recalculated the median values. Figure 4 shows the results, where the circular points are the median values of the difference in fluxes between the 2- and 0.4-s frame-times for both the full-array only data (blue) and the subarray only data (red). The bright and faint subsets are shown with the appropriately colored triangles. The differences between the bright and faint samples are within one sigma of each other. Here, sigma is calculated as the standard deviation between stars, which means that each bin contains only a few stars (and not thousands of data points). Our sample size is not large enough to make conclusions based on star brightness.

3.3.

Disentangling Exposure Time and Array Mode Effects

We examine the possibility of disentangling the effects of exposure time and array mode. Instead of dividing the dataset by star, here we consider all stellar photometry as a single dataset and divide the dataset into four categories depending on the combination of array mode (full array versus subarray) and exposure time (short versus long). Each distribution has between 3000 and 50,000 stars (subarray exposure times have lots more frames than full array). Exact exposure times cannot be compared in this analysis because they differ significantly for full and subarray modes (see Table 1). For this reason, the division between the short and long exposure times is set at 0.3 s to construct statistically significant samples.

Figure 5 reveals differences between the overall distributions of photometry taken in full and subarray modes while accounting for exposure time, with enough data points to accurately reflect the shapes of the distributions. Longer exposure times are in red and light blue; shorter exposure times are in orange and dark blue. Especially at [3.6], an effect is apparent with both exposure time and observing mode. For the stars that have full-array observations in both short and long exposure times, the median difference in the flux is 3.4% at [3.6] (for six stars) and 0.6% at [4.5] (for 10 stars). For subarray, we find the median difference in flux between short and long exposure times to be 2.9% at [3.6] and 1.5% at [4.5].

Fig. 5

Distribution of normalized star fluxes for (a) [3.6] and (b) [4.5]. The legend lists the different observing modes (full array versus subarray and long exposure times versus short exposure times) as well as the mean well depth per distribution. Solid dark lines show the kernel density estimation overplotted on the histograms. We see a difference in the absolute photometry of stars taken in available observing modes and exposure times shown here in the colored distributions.

3.4.

Well Depth

The legend to Fig. 5 lists median well depths for each of the distributions. Well depth is one physical feature that correlates with the difference between short and long and full and subarray exposures. We do expect that longer exposure times on the same set of stars will have larger fractional well depths, so it makes sense that the full long and sublong distributions have the larger median well depths in both channels. Also, subarray mode has the possibility of shorter frame times than full array, so we would expect that subarray would have lower well depths than full array. Both channels show this behavior.

Figure 6 shows the distributions of normalized fluxes for the entire sample of stars in [3.6] and [4.5] divided into three well-depth bins. These bins do not have the same number of photometry points in them as we have many more low well-depth observations than intermediate well-depth observations. Because of this change in the number of data points per bin, we do not quote values for the peak of each bin, but rather address the trends revealed by the data in hand [3.6] shows a clear trend such that observations at intermediate well depths have lower normalized fluxes. [4.5] shows little, if any trend, consistent with trends seen in the observing mode and exposure time plots. While there are sources at higher well depth than 50% full well, their distribution overlaps those of the 20% to 50% bin. We conclude that only fractional well-depths less than a few tens of percent are affected by this well-depth effect. Consideration of well-depth does not help to disentangle the effects we have seen with observing mode and exposure time, but it is a clue that potentially the source of some of what we are seeing is nonlinearity in the low well-depth regime.

Fig. 6

Distributions of fluxes in three fractional well depth bins for (a) [3.6] and (b) [4.5]. Colors for the distributions get darker as the fractional well depth increases.

3.5.

Dithering versus Staring-Mode

We do not detect a difference in photometry between the dithered and staring-mode observations. For three stars, we have observations in all the modes for the 2-s exposure times (substaring, subdithering, full staring, and full dithering). Recall that subarray observations taken with 2-s frame-time have 1.92-s exposure times and 2-s frame time full-array observations have 1.2-s effective exposure time, so the 2-s exposure time subarray and full array observations are not equivalent, but they are the closest to equivalent that exist in the archive.

Figure 7 shows a Cleveland dot plot of the median and standard deviation of the normalized fluxes for each mode, for each of the three stars in this sample. The legend also lists the number of data points per mode. The full and subarray measurements differ as before (see Sec. 3.1). The staring-mode photometry is consistent with the dithered mode photometry within one sigma in both channels.

Fig. 7

Cleveland dot plot comparing normalized fluxes from different observing modes and dithering versus staring for three stars listed on the y-axis. (a) [3.6] and (b) [4.5]. The legend is for both plots and lists the number of data points for each mode.

3.6.

Multiple Regression

Finding a relation among the observing parameters (array mode, exposure time, staring/dithering) may help both to (a) understand the effects found in this paper and (b) correct for them. We therefore use the statistical technique of multiple regression to search for any relations. Specifically, we used multiple linear regression, i.e., multiple independent variables, to predict the value of the dependent variable. To correct IRAC photometry for these effects, we have tried ordinary least squares (OLS) as a multiple linear-regression technique. We used array mode, exposure time, and stare/dither as independent variables, and flux as the dependent variable. We used two different modules in Python for this work: statsmodels¹¹ and sklearn.¹² We are unable to find successful models. The $R^2$ goodness of fit is 0.037, when “good” models should have values close to 1.0. The failure of OLS in this situation could imply that the relationship between the independent and dependent variables is nonlinear.