§4.2 Definitions
Contents
- §4.2(i) The Logarithm
- §4.2(ii) Logarithms to a General Base
- §4.2(iii) The Exponential Function
- §4.2(iv) Powers
§4.2(i) The Logarithm
The general logarithm function is defined by
| 4.2.1 | |||
| , | |||
where the integration path does not intersect the origin. This is a multivalued function of with branch point at .
The principal value, or principal branch, is defined by
| 4.2.2 | |||
where the path does not intersect ; see Figure 4.2.1. is a single-valued analytic function on and real-valued when ranges over the positive real numbers.
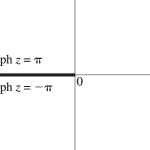
The only zero of is at .
Most texts extend the definition of the principal value to include the branch cut
| 4.2.4 | |||
| , | |||
by replacing (4.2.3) with
| 4.2.5 | |||
| . | |||
With this definition the general logarithm is given by
| 4.2.6 | |||
where is the excess of the number of times the path in (4.2.1) crosses the negative real axis in the positive sense over the number of times in the negative sense.
In the DLMF we allow a further extension by regarding the cut as representing two sets of points, one set corresponding to the “upper side” and denoted by , the other set corresponding to the “lower side” and denoted by . Again see Figure 4.2.1. Then
| 4.2.7 | |||
| , | |||
with either upper signs or lower signs taken throughout. Consequently is two-valued on the cut, and discontinuous across the cut. We regard this as the closed definition of the principal value.
In contrast to (4.2.5) the closed definition is symmetric. As a consequence, it has the advantage of extending regions of validity of properties of principal values. For example, with the definition (4.2.5) the identity (4.8.7) is valid only when , but with the closed definition the identity (4.8.7) is valid when . For another example see (4.2.37).
§4.2(ii) Logarithms to a General Base
With or ,
| 4.2.8 | ||||
| 4.2.9 | ||||
| 4.2.10 | ||||
Natural logarithms have as base the unique positive number
| 4.2.11 | |||
such that
| 4.2.12 | |||
Equivalently,
| 4.2.13 | |||
Thus
| 4.2.14 | |||
| 4.2.15 | |||
| 4.2.16 | |||
| 4.2.17 | |||
| 4.2.18 | |||
is also called the Napierian or hyperbolic logarithm. is the common or Briggs logarithm.
§4.2(iii) The Exponential Function
| 4.2.19 | |||
The function is an entire function of , with no real or complex zeros. It has period :
| 4.2.20 | |||
Also,
| 4.2.21 | |||
| 4.2.22 | |||
The general value of the phase is given by
| 4.2.23 | |||
| . | |||
If , then
| 4.2.24 | |||
If then
| 4.2.25 | |||
§4.2(iv) Powers
Powers with General Bases
The general power of is defined by
| 4.2.26 | |||
| . | |||
In particular, , and if , then
| 4.2.27 | |||
In all other cases, is a multivalued function with branch point at . The principal value is
| 4.2.28 | |||
This is an analytic function of on , and is two-valued and discontinuous on the cut shown in Figure 4.2.1, unless .
| 4.2.29 | |||
| 4.2.30 | |||
where for the principal value of , and is unrestricted in the general case. When is real
| 4.2.31 | ||||
Unless indicated otherwise, it is assumed throughout the DLMF that a power assumes its principal value. With this convention,
| 4.2.32 | |||
but the general value of is
| 4.2.33 | |||
| . | |||
For
| 4.2.34 | |||
If has its general value, with , and if , then
| 4.2.35 | |||
This result is also valid when has its principal value, provided that the branch of satisfies
| 4.2.36 | |||
Another example of a principal value is provided by
| 4.2.37 | |||
Again, without the closed definition the and signs would have to be replaced by and , respectively.
