§25.12 Polylogarithms

ⓘ

Notes:: See Maximon (2003), Lewin (1981), Dingle (1957a), and Dingle (1957b).
Permalink:: http://dlmf.nist.gov/25.12
See also:: Annotations for Ch.25

§25.12(i) Dilogarithms
§25.12(ii) Polylogarithms
§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

§25.12(i) Dilogarithms

ⓘ

Keywords:: Clausen’s integral, analytic properties, definition, dilogarithms, graphics, principal branch (or value)
Notes:: See Maximon (2003, pp. 2807–2813). The graphics were constructed at NIST.
Referenced by:: 2nd item, 4th item, §25.21(vi)
Permalink:: http://dlmf.nist.gov/25.12.i
See also:: Annotations for §25.12 and Ch.25

The notation $\operatorname{Li}_{2}\left(z\right)$ was introduced in Lewin (1981) for a function discussed in Euler (1768) and called the dilogarithm in Hill (1828):

25.12.1		$\operatorname{Li}_{2}\left(z\right)\equiv\sum_{n=1}^{\infty}\frac{z^{n}}{n^{2}},$
$\|z\|\leq 1$ .
ⓘ Defines: $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm Symbols: $\equiv$ : equals by definition, $n$ : nonnegative integer, $x$ : real variable and $z$ : complex variable Keywords: definition Source: Maximon (2003, (3.1), p. 2808) A&S Ref: 27.7.2 (with $z=1-x$ ) Referenced by: §25.12(i), §25.12(i) Permalink: http://dlmf.nist.gov/25.12.E1 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

25.12.2		$\operatorname{Li}_{2}\left(z\right)=-\int_{0}^{z}t^{-1}\ln\left(1-t\right)\,% \mathrm{d}t,$
$z\in\mathbb{C}\setminus(1,\infty)$ .
ⓘ Symbols: $\mathbb{C}$ : complex plane, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\in$ : element of, $\int$ : integral, $\ln\NVar{z}$ : principal branch of logarithm function, $(\NVar{a},\NVar{b})$ : open interval, $\setminus$ : set subtraction, $x$ : real variable and $z$ : complex variable Keywords: definite integral, integral representation Source: Maximon (2003, (2.1), p. 2807) A&S Ref: 27.7.1 (is a modified form with $z=1-x$ ) Referenced by: §25.12(i) Permalink: http://dlmf.nist.gov/25.12.E2 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

Other notations and names for $\operatorname{Li}_{2}\left(z\right)$ include $S_{2}(z)$ (Kölbig et al. (1970)), Spence function $\mathrm{Sp}(z)$ (’t Hooft and Veltman (1979)), and $\mathrm{L}_{2}(z)$ (Maximon (2003)).

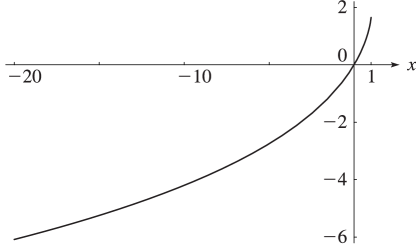
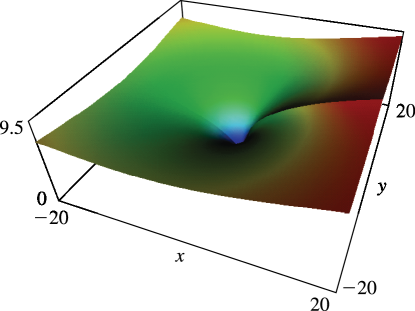
In the complex plane $\operatorname{Li}_{2}\left(z\right)$ has a branch point at $z=1$ . The principal branch has a cut along the interval $[1,\infty)$ and agrees with (25.12.1) when $|z|\leq 1$ ; see also §4.2(i). The remainder of the equations in this subsection apply to principal branches.

25.12.3		$\operatorname{Li}_{2}\left(z\right)+\operatorname{Li}_{2}\left(\frac{z}{z-1}% \right)=-\frac{1}{2}(\ln\left(1-z\right))^{2},$
$z\in\mathbb{C}\setminus[1,\infty)$ .
ⓘ Symbols: $[\NVar{a},\NVar{b})$ : half-closed interval, $\mathbb{C}$ : complex plane, $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\in$ : element of, $\ln\NVar{z}$ : principal branch of logarithm function, $\setminus$ : set subtraction, $x$ : real variable and $z$ : complex variable Keywords: connection formula Source: Maximon (2003, (3.4), p. 2808) A&S Ref: 27.7.5 (is a modified form with $z=1-x$ ) Permalink: http://dlmf.nist.gov/25.12.E3 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

25.12.4		$\operatorname{Li}_{2}\left(z\right)+\operatorname{Li}_{2}\left(\frac{1}{z}% \right)=-\frac{1}{6}\pi^{2}-\frac{1}{2}(\ln\left(-z\right))^{2},$
$z\in\mathbb{C}\setminus[0,\infty)$ .
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $[\NVar{a},\NVar{b})$ : half-closed interval, $\mathbb{C}$ : complex plane, $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\in$ : element of, $\ln\NVar{z}$ : principal branch of logarithm function, $\setminus$ : set subtraction and $z$ : complex variable Keywords: connection formula Source: Maximon (2003, (3.2), p. 2808) Referenced by: §25.12(ii) Permalink: http://dlmf.nist.gov/25.12.E4 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

25.12.5		$\operatorname{Li}_{2}\left(z^{m}\right)=m\sum_{k=0}^{m-1}\operatorname{Li}_{2}% \left(ze^{2\pi ik/m}\right),$
$m=1,2,3,\dots$ , $\|z\|<1$ .
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\mathrm{e}$ : base of natural logarithm, $\mathrm{i}$ : imaginary unit, $k$ : nonnegative integer, $m$ : nonnegative integer and $z$ : complex variable Source: Maximon (2003, (3.12), p. 2809) Permalink: http://dlmf.nist.gov/25.12.E5 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

25.12.6		$\operatorname{Li}_{2}\left(x\right)+\operatorname{Li}_{2}\left(1-x\right)=% \frac{1}{6}\pi^{2}-(\ln x)\ln\left(1-x\right),$
$0<x<1$ .
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\ln\NVar{z}$ : principal branch of logarithm function and $x$ : real variable Keywords: connection formula Source: Maximon (2003, (3.3), p. 2808) Permalink: http://dlmf.nist.gov/25.12.E6 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

When $z=e^{i\theta}$ , $0\leq\theta\leq 2\pi$ , (25.12.1) becomes

25.12.7		$\operatorname{Li}_{2}\left(e^{i\theta}\right)=\sum_{n=1}^{\infty}\frac{\cos% \left(n\theta\right)}{n^{2}}+i\sum_{n=1}^{\infty}\frac{\sin\left(n\theta\right% )}{n^{2}}.$
ⓘ Symbols: $\cos\NVar{z}$ : cosine function, $\operatorname{Li}_{2}\left(\NVar{z}\right)$ : dilogarithm, $\mathrm{e}$ : base of natural logarithm, $\mathrm{i}$ : imaginary unit, $\sin\NVar{z}$ : sine function, $n$ : nonnegative integer and $\theta$ : phase Keywords: infinite series, series representation Source: Maximon (2003, (8.7), p. 2813) Referenced by: §25.12(i) Permalink: http://dlmf.nist.gov/25.12.E7 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

The cosine series in (25.12.7) has the elementary sum

25.12.8		$\sum_{n=1}^{\infty}\frac{\cos\left(n\theta\right)}{n^{2}}=\frac{\pi^{2}}{6}-% \frac{\pi\theta}{2}+\frac{\theta^{2}}{4}.$
ⓘ Symbols: $\pi$ : the ratio of the circumference of a circle to its diameter, $\cos\NVar{z}$ : cosine function, $n$ : nonnegative integer and $\theta$ : phase Keywords: infinite series Source: Maximon (2003, (8.7), p. 2813) A&S Ref: 27.8.6 (second series) Permalink: http://dlmf.nist.gov/25.12.E8 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

By (25.12.2)

25.12.9		$\sum_{n=1}^{\infty}\frac{\sin\left(n\theta\right)}{n^{2}}=-\int_{0}^{\theta}% \ln\left(2\sin\left(\tfrac{1}{2}x\right)\right)\,\mathrm{d}x.$
ⓘ Symbols: $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\int$ : integral, $\ln\NVar{z}$ : principal branch of logarithm function, $\sin\NVar{z}$ : sine function, $n$ : nonnegative integer, $x$ : real variable and $\theta$ : phase Keywords: definite integral, infinite series Source: Maximon (2003, (8.7), (8.8), p. 2813) A&S Ref: 27.8.6 (integration of first series) Referenced by: 1st item Permalink: http://dlmf.nist.gov/25.12.E9 Encodings: TeX, pMML, png See also: Annotations for §25.12(i), §25.12 and Ch.25

The right-hand side is called Clausen’s integral.

For graphics see Figures 25.12.1 and 25.12.2, and for further properties see Maximon (2003), Kirillov (1995), Lewin (1981), Nielsen (1909), and Zagier (1989).

See accompanying text — Figure 25.12.1: Dilogarithm function $\operatorname{Li}_{2}\left(x\right)$ , $-20\leq x<1.$ Magnify 3D Help

§25.12(ii) Polylogarithms

ⓘ

Defines:: $\phi\left(\NVar{z},\NVar{s}\right)=\operatorname{Li}_{s}\left(z\right)$ : notation used by (Truesdell, 1945)
Keywords:: Riemann zeta function, analytic properties, definitions, polylogarithms, relations to other functions, series expansions
Notes:: See Lewin (1981, Section 7.12).
Referenced by:: §25.14(i)
Permalink:: http://dlmf.nist.gov/25.12.ii
See also:: Annotations for §25.12 and Ch.25

For real or complex $s$ and $z$ the polylogarithm $\operatorname{Li}_{s}\left(z\right)$ is defined by

25.12.10		$\operatorname{Li}_{s}\left(z\right)=\sum_{n=1}^{\infty}\frac{z^{n}}{n^{s}}.$
ⓘ Defines: $\operatorname{Li}_{\NVar{s}}\left(\NVar{z}\right)$ : polylogarithm Symbols: $n$ : nonnegative integer, $s$ : complex variable and $z$ : complex variable Keywords: definition, infinite series, series representation Source: Lewin (1981, p. 236) Referenced by: (25.14.3) Permalink: http://dlmf.nist.gov/25.12.E10 Encodings: TeX, pMML, png See also: Annotations for §25.12(ii), §25.12 and Ch.25

For each fixed complex $s$ the series defines an analytic function of $z$ for $|z|<1$ . The series also converges when $|z|=1$ , provided that $\Re s>1$ . For other values of $z$ , $\operatorname{Li}_{s}\left(z\right)$ is defined by analytic continuation.

The notation $\phi\left(z,s\right)$ was used for $\operatorname{Li}_{s}\left(z\right)$ in Truesdell (1945) for a series treated in Jonquière (1889), hence the alternative name Jonquière’s function. The special case $z=1$ is the Riemann zeta function: $\zeta\left(s\right)=\operatorname{Li}_{s}\left(1\right)$ .

Integral Representation

ⓘ

Keywords:: Hurwitz zeta function, Riemann zeta function, integral representations, polylogarithms, relations to other functions
See also:: Annotations for §25.12(ii), §25.12 and Ch.25

25.12.11		$\operatorname{Li}_{s}\left(z\right)\equiv\frac{z}{\Gamma\left(s\right)}\int_{0% }^{\infty}\frac{x^{s-1}}{e^{x}-z}\,\mathrm{d}x,$
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\equiv$ : equals by definition, $\mathrm{e}$ : base of natural logarithm, $\int$ : integral, $\operatorname{Li}_{\NVar{s}}\left(\NVar{z}\right)$ : polylogarithm, $x$ : real variable, $s$ : complex variable and $z$ : complex variable Keywords: improper integral, integral representation Source: Lewin (1981, (7.188), p. 236) Referenced by: (25.12.16), §25.12(ii) Permalink: http://dlmf.nist.gov/25.12.E11 Encodings: TeX, pMML, png See also: Annotations for §25.12(ii), §25.12(ii), §25.12 and Ch.25

valid when $\Re s>0$ and $\left|\operatorname{ph}\left(1-z\right)\right|<\pi$ , or $\Re s>1$ and $z=1$ . (In the latter case (25.12.11) becomes (25.5.1)).

Further properties include

25.12.12		$\operatorname{Li}_{s}\left(z\right)=\Gamma\left(1-s\right)\left(\ln\frac{1}{z}% \right)^{s-1}+\sum_{n=0}^{\infty}\zeta\left(s-n\right)\frac{(\ln z)^{n}}{n!},$
$s\neq 1,2,3,\dots$ , $\|\ln z\|<2\pi$ ,
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\zeta\left(\NVar{s}\right)$ : Riemann zeta function, $\pi$ : the ratio of the circumference of a circle to its diameter, $!$ : factorial (as in $n!$ ), $\ln\NVar{z}$ : principal branch of logarithm function, $\operatorname{Li}_{\NVar{s}}\left(\NVar{z}\right)$ : polylogarithm, $n$ : nonnegative integer, $s$ : complex variable and $z$ : complex variable Keywords: infinite series, series representation Source: Erdélyi et al. (1953a, (1.11.8), p. 29); take $v=1$ and use (25.14.3), (25.11.2) Permalink: http://dlmf.nist.gov/25.12.E12 Encodings: TeX, pMML, png See also: Annotations for §25.12(ii), §25.12(ii), §25.12 and Ch.25

and

25.12.13		$\operatorname{Li}_{s}\left(e^{2\pi ia}\right)+e^{\pi is}\operatorname{Li}_{s}% \left(e^{-2\pi ia}\right)=\frac{(2\pi)^{s}e^{\pi is/2}}{\Gamma\left(s\right)}% \zeta\left(1-s,a\right),$
ⓘ Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\zeta\left(\NVar{s},\NVar{a}\right)$ : Hurwitz zeta function, $\pi$ : the ratio of the circumference of a circle to its diameter, $\mathrm{e}$ : base of natural logarithm, $\mathrm{i}$ : imaginary unit, $(\NVar{a},\NVar{b})$ : open interval, $\operatorname{Li}_{\NVar{s}}\left(\NVar{z}\right)$ : polylogarithm, $a$ : real or complex parameter, $s$ : complex variable and $z$ : complex variable Source: Erdélyi et al. (1953a, (1.11.16), p. 31); with $\operatorname{Li}_{s}\left(z\right)=F(z,s)$ , $z={\mathrm{e}}^{2\pi\mathrm{i}a}$ Referenced by: §25.12(ii) Permalink: http://dlmf.nist.gov/25.12.E13 Encodings: TeX, pMML, png See also: Annotations for §25.12(ii), §25.12(ii), §25.12 and Ch.25

valid when $\Re s>0$ , $\Im a>0$ or $\Re s>1$ , $\Im a=0$ . When $s=2$ and $e^{2\pi ia}=z$ , (25.12.13) becomes (25.12.4).

See also Lewin (1981), Kölbig (1986), Maximon (2003), Prudnikov et al. (1990, §§1.2 and 2.5), Prudnikov et al. (1992a, §3.3), and Prudnikov et al. (1992b, §3.3).

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals

ⓘ

Keywords:: Bose–Einstein integrals, Fermi–Dirac integrals, definition, polylogarithms, relation to polylogarithms, relations to other functions, uniform asymptotic approximation
Notes:: See Dingle (1957a) and Dingle (1957b).
Permalink:: http://dlmf.nist.gov/25.12.iii
See also:: Annotations for §25.12 and Ch.25

The Fermi–Dirac and Bose–Einstein integrals are defined by

25.12.14	$\displaystyle F_{s}(x)$	$\displaystyle=\frac{1}{\Gamma\left(s+1\right)}\int_{0}^{\infty}\frac{t^{s}}{e^% {t-x}+1}\,\mathrm{d}t,$
$s>-1$ ,
ⓘ Defines: $F_{s}(x)$ : Fermi–Dirac integral (locally) Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\int$ : integral, $x$ : real variable and $s$ : complex variable Keywords: Fermi–Dirac integral, definition, improper integral, integral representation Source: Dingle (1957b, (1), p. 226) Referenced by: (25.12.16), 3rd item, 5th item Permalink: http://dlmf.nist.gov/25.12.E14 Encodings: TeX, pMML, png See also: Annotations for §25.12(iii), §25.12 and Ch.25
25.12.15	$\displaystyle G_{s}(x)$	$\displaystyle=\frac{1}{\Gamma\left(s+1\right)}\int_{0}^{\infty}\frac{t^{s}}{e^% {t-x}-1}\,\mathrm{d}t,$
$s>-1$ , $x<0$ ; or $s>0$ , $x\leq 0$ ,
ⓘ Defines: $G_{s}(x)$ : Bose–Einstein integral (locally) Symbols: $\Gamma\left(\NVar{z}\right)$ : gamma function, $\,\mathrm{d}\NVar{x}$ : differential of $x$ , $\mathrm{e}$ : base of natural logarithm, $\int$ : integral, $x$ : real variable and $s$ : complex variable Keywords: Bose–Einstein integral, definition, improper integral, integral representation Source: Dingle (1957a, p. 240) Referenced by: (25.12.16) Permalink: http://dlmf.nist.gov/25.12.E15 Encodings: TeX, pMML, png See also: Annotations for §25.12(iii), §25.12 and Ch.25

respectively. Sometimes the factor $1/\Gamma\left(s+1\right)$ is omitted. See Cloutman (1989) and Gautschi (1993).

In terms of polylogarithms

25.12.16	$\displaystyle F_{s}(x)$	$\displaystyle=-\operatorname{Li}_{s+1}\left(-e^{x}\right),$
25.12.16	$\displaystyle G_{s}(x)$	$\displaystyle=\operatorname{Li}_{s+1}\left(e^{x}\right).$
ⓘ Symbols: $\mathrm{e}$ : base of natural logarithm, $\operatorname{Li}_{\NVar{s}}\left(\NVar{z}\right)$ : polylogarithm, $x$ : real variable, $s$ : complex variable, $F_{s}(x)$ : Fermi–Dirac integral and $G_{s}(x)$ : Bose–Einstein integral Proof sketch: Derivable from (25.12.11), (25.12.14), (25.12.15). Permalink: http://dlmf.nist.gov/25.12.E16 Encodings: TeX, TeX, pMML, pMML, png, png See also: Annotations for §25.12(iii), §25.12 and Ch.25

For a uniform asymptotic approximation for $F_{s}(x)$ see Temme and Olde Daalhuis (1990).

25.11 Hurwitz Zeta Function 25.13 Periodic Zeta Function

Site Privacy Accessibility Privacy Program Copyrights Vulnerability Disclosure No Fear Act Policy FOIA Environmental Policy Scientific Integrity Information Quality Standards Commerce.gov Science.gov USA.gov

§25.12 Polylogarithms

Contents

§25.12(i) Dilogarithms

§25.12(ii) Polylogarithms

Integral Representation

§25.12(iii) Fermi–Dirac and Bose–Einstein Integrals