§20.3 Graphics
Contents
- §20.3(i) -Functions: Real Variable and Real Nome
- §20.3(ii) -Functions: Complex Variable and Real Nome
- §20.3(iii) -Functions: Real Variable and Complex Lattice Parameter
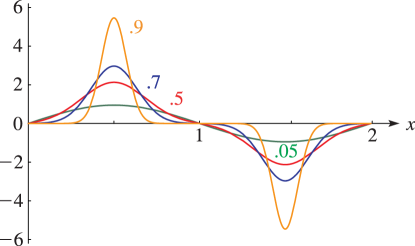
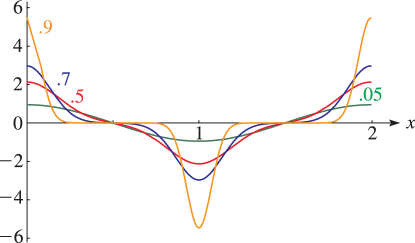
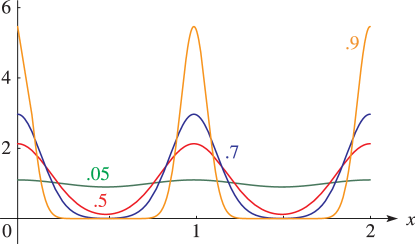
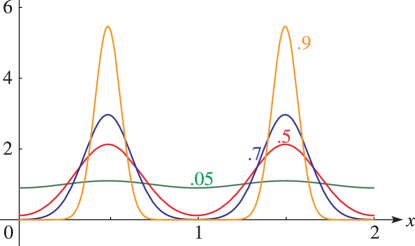
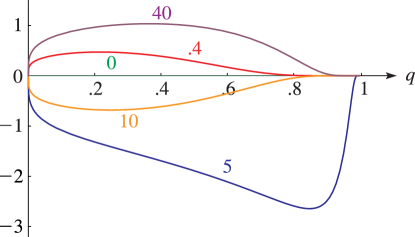
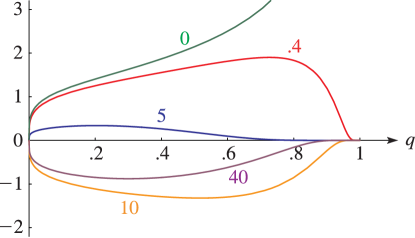
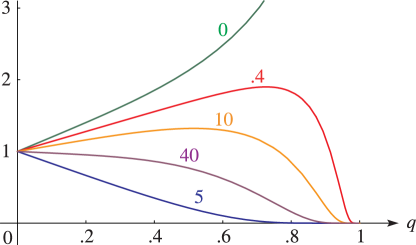
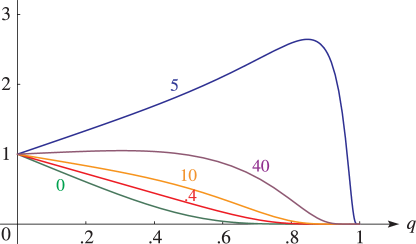
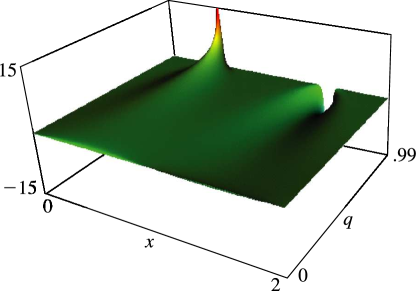
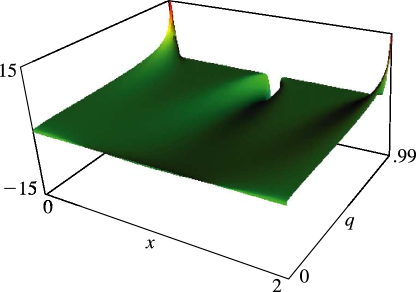
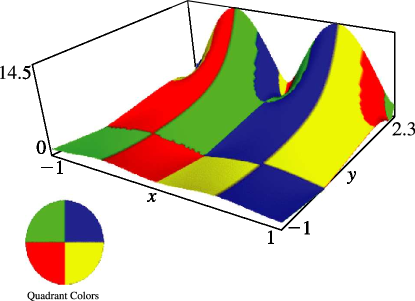
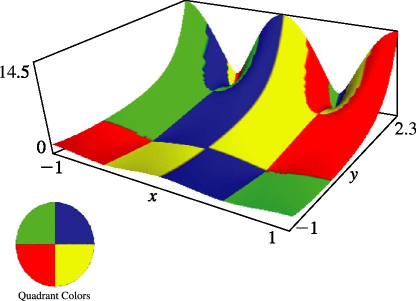
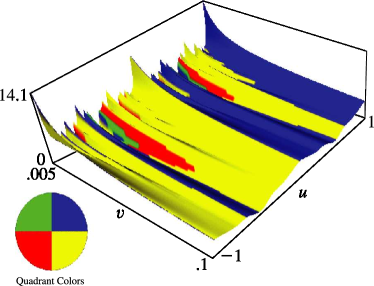
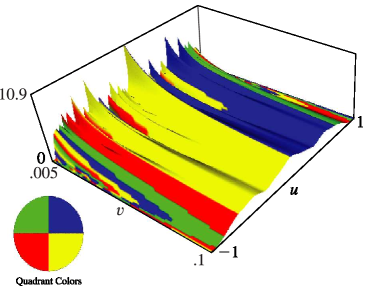
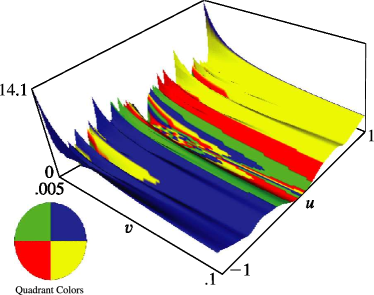
§20.3(i) -Functions: Real Variable and Real Nome
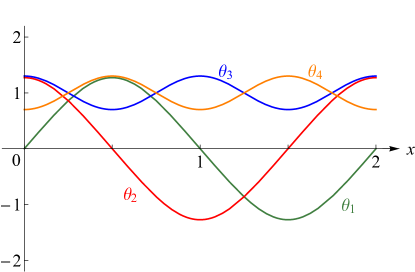
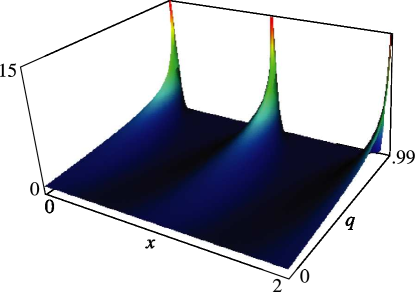
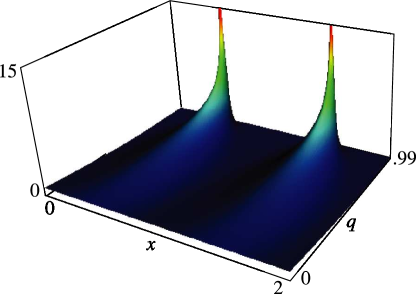
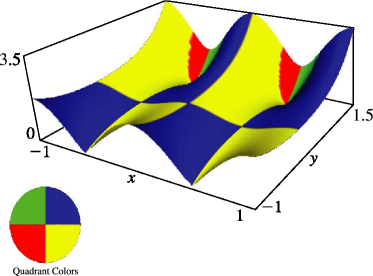
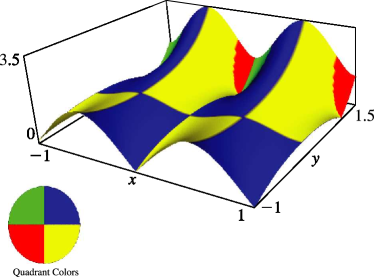
§20.3(ii) -Functions: Complex Variable and Real Nome
In the graphics shown in this subsection, height corresponds to the absolute value of the function and color to the phase. See also About Color Map.
§20.3(iii) -Functions: Real Variable and Complex Lattice Parameter
In the graphics shown in this subsection, height corresponds to the absolute value of the function and color to the phase. See also About Color Map.