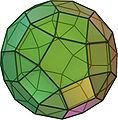
Deltoidalhexakontaeder

Das Deltoidalhexakontaeder (auch Deltoidhexakontaeder genannt) ist ein konvexes Polyeder, das sich aus 60 Deltoiden zusammensetzt und zu den Catalanischen Körpern zählt. Es ist dual zum Rhombenikosidodekaeder und hat 62 Ecken sowie 120 Kanten.

Entstehung

Konstruktion des Deltoids am Rhombenikosidodekaeder

Durch Verbinden der Mittelpunkte vierer Kanten, die in jeder Raumecke des Rhombenikosidodekaeders zusammenstoßen, entsteht ein Trapez, dessen Umkreis gleichzeitig Inkreis des Deltoids, der Begrenzungsfläche des Deltoidalhexakontaeders, ist. Bei diesem speziellen Typ sind alle Flächenwinkel gleich groß (≈ 154°), und es existiert ein einheitlicher Kantenkugelradius.

Sei $d$ die Kantenlänge des Rhombenikosidodekaeders, so sind die resultierenden Seitenlängen des Deltoids gegeben durch

a=\,{\frac {d}{3}}\,{\sqrt {25-5{\sqrt {5}}}}

b=\,{\frac {d}{11}}\,{\sqrt {5\,(85-31{\sqrt {5}})}}

Die Seitenlängen des Deltoids stehen somit im folgenden Verhältnis zueinander:^[1]

3a\,(7-{\sqrt {5}})=22b

Formeln

Für das Polyeder

Größen eines Deltoidalhexakontaeders mit Kantenlänge a
Volumen	$V={\frac {45}{11}}\,a^{3}{\sqrt {\frac {370+164{\sqrt {5}}}{25}}}$
Oberflächeninhalt	$A_{O}={\frac {9}{11}}\,a^{2}{\sqrt {10\,(157+31{\sqrt {5}})}}$
Inkugelradius	$\rho ={\frac {3}{2}}\,a\,{\sqrt {\frac {135+59{\sqrt {5}}}{205}}}$
Kantenkugelradius	$r={\frac {3}{20}}\,a\,(5+3{\sqrt {5}})$
Flächenwinkel ≈ 154° 7′ 17″	$\cos \,\alpha =-{\frac {1}{41}}\,(19+8{\sqrt {5}})$
3D-Kantenwinkel ≈ 153° 26′ 6″	$\cos \,\gamma =-{\frac {2}{5}}{\sqrt {5}}$
Sphärizität ≈ 0,98161	$\Psi ={\frac {2\,{\sqrt[{3}]{11\,\pi \left(185+82{\sqrt {5}}\right)}}}{\sqrt {10\left(157+31{\sqrt {5}}\right)}}}$

Für das Deltoid

Größen des Drachenvierecks
Flächeninhalt	$A={\frac {3}{22}}\,a^{2}{\sqrt {\frac {157+31{\sqrt {5}}}{10}}}$
2. Seitenlänge	$b={\frac {3}{22}}\,a\,(7-{\sqrt {5}})$
Kurze Diagonale	$e=3a\,{\sqrt {\frac {5-{\sqrt {5}}}{20}}}$
Lange Diagonale	$f={\frac {a}{11}}{\sqrt {\frac {470+156{\sqrt {5}}}{5}}}$
Inkreisradius	$r={\frac {3}{10}}\,a\,{\sqrt {\frac {5\,(17+5{\sqrt {5}})}{82}}}$
Seitenwinkel (2) ≈ 86° 58′ 27″	$\cos \,\alpha ={\frac {1}{10}}\,(5-2{\sqrt {5}})$
Fußwinkel (1) ≈ 67° 46′ 59″	$\cos \,\beta ={\frac {1}{40}}\,(9{\sqrt {5}}-5)$
Kopfwinkel (1) ≈ 118° 16′ 7″	$\cos \,\gamma =-{\frac {1}{20}}\,(5+2{\sqrt {5}})$