What is Stack Data Structure? A Complete Tutorial
Last Updated :
06 Jun, 2024
Stack Data Structure is a linear data structure that follows LIFO (Last In First Out) Principle , so the last element inserted is the first to be popped out. In this article, we will cover all the basics of Stack, Operations on Stack, its implementation, advantages, disadvantages which will help you solve all the problems based on Stack.
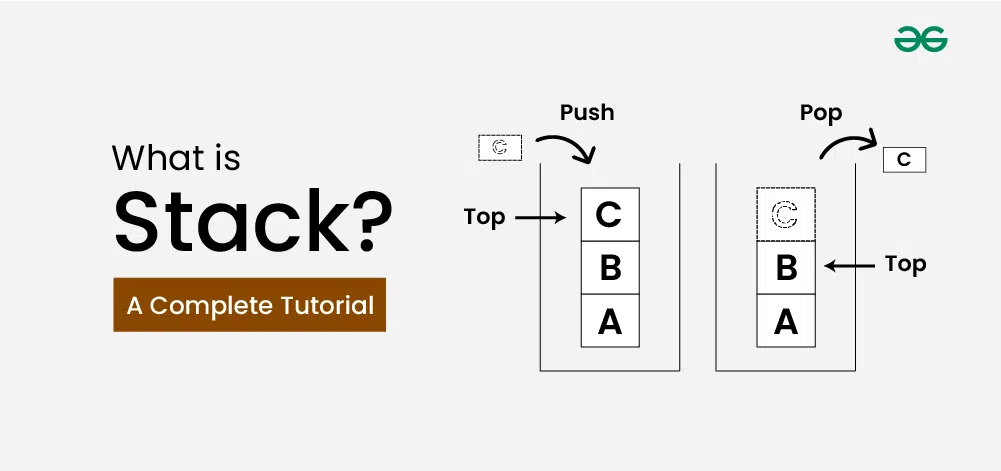
What is Stack Data Structure?
Stack is a linear data structure based on LIFO(Last In First Out) principle in which the insertion of a new element and removal of an existing element takes place at the same end represented as the top of the stack.
To implement the stack, it is required to maintain the pointer to the top of the stack , which is the last element to be inserted because we can access the elements only on the top of the stack.
LIFO(Last In First Out) Principle in Stack Data Structure:
This strategy states that the element that is inserted last will come out first. You can take a pile of plates kept on top of each other as a real-life example. The plate which we put last is on the top and since we remove the plate that is at the top, we can say that the plate that was put last comes out first.
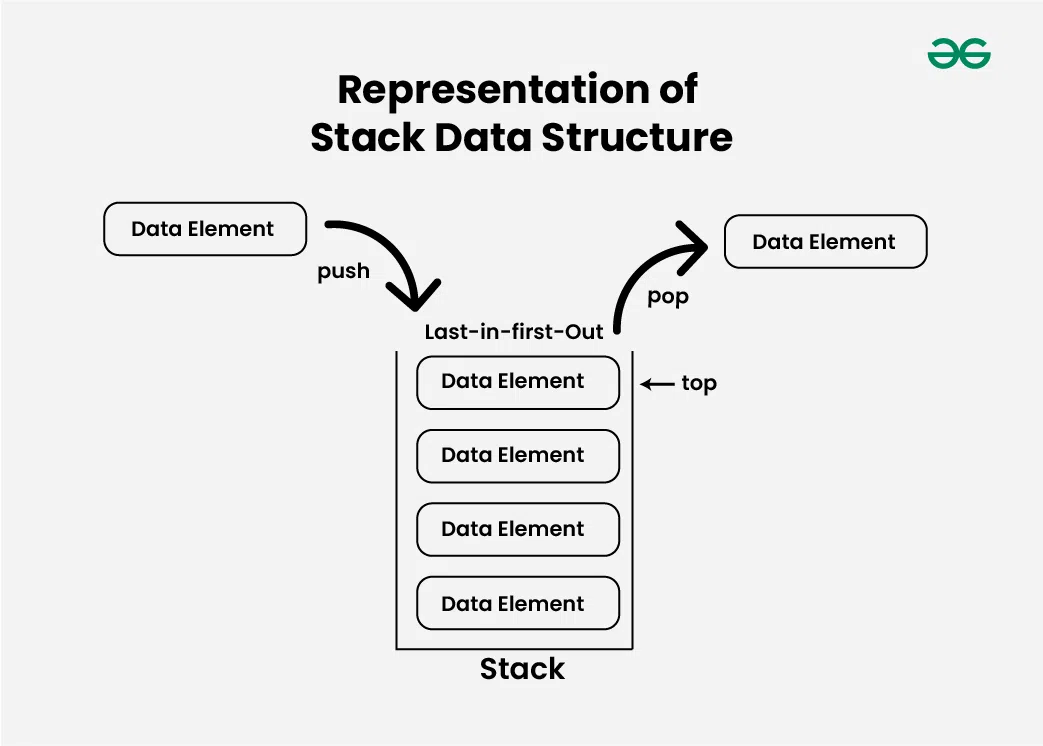
Representation of Stack Data Structure:
Stack follows LIFO (Last In First Out) Principle so the element which is pushed last is popped first.
Types of Stack Data Structure:
- Fixed Size Stack : As the name suggests, a fixed size stack has a fixed size and cannot grow or shrink dynamically. If the stack is full and an attempt is made to add an element to it, an overflow error occurs. If the stack is empty and an attempt is made to remove an element from it, an underflow error occurs.
- Dynamic Size Stack : A dynamic size stack can grow or shrink dynamically. When the stack is full, it automatically increases its size to accommodate the new element, and when the stack is empty, it decreases its size. This type of stack is implemented using a linked list, as it allows for easy resizing of the stack.
Basic Operations on Stack Data Structure:
In order to make manipulations in a stack, there are certain operations provided to us.
- push() to insert an element into the stack
- pop() to remove an element from the stack
- top() Returns the top element of the stack.
- isEmpty() returns true if stack is empty else false.
- isFull() returns true if the stack is full else false.
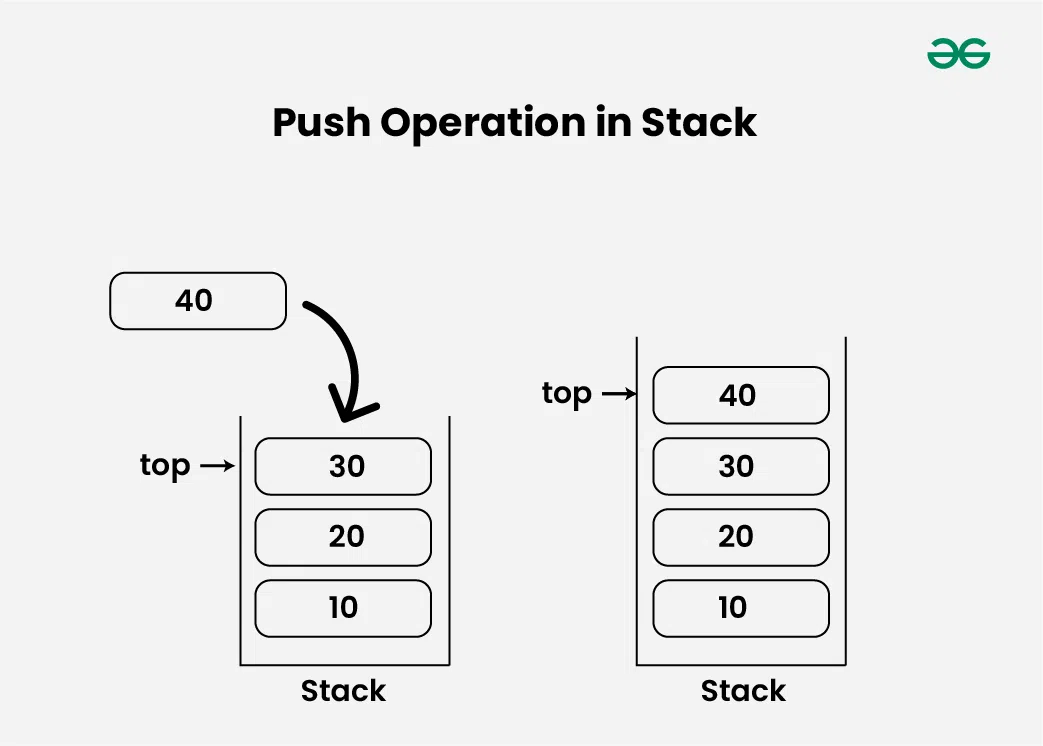
Push Operation in Stack Data Structure:
Adds an item to the stack. If the stack is full, then it is said to be an Overflow condition.
Algorithm for Push Operation:
- Before pushing the element to the stack, we check if the stack is full .
- If the stack is full (top == capacity-1) , then Stack Overflows and we cannot insert the element to the stack.
- Otherwise, we increment the value of top by 1 (top = top + 1) and the new value is inserted at top position .
- The elements can be pushed into the stack till we reach the capacity of the stack.
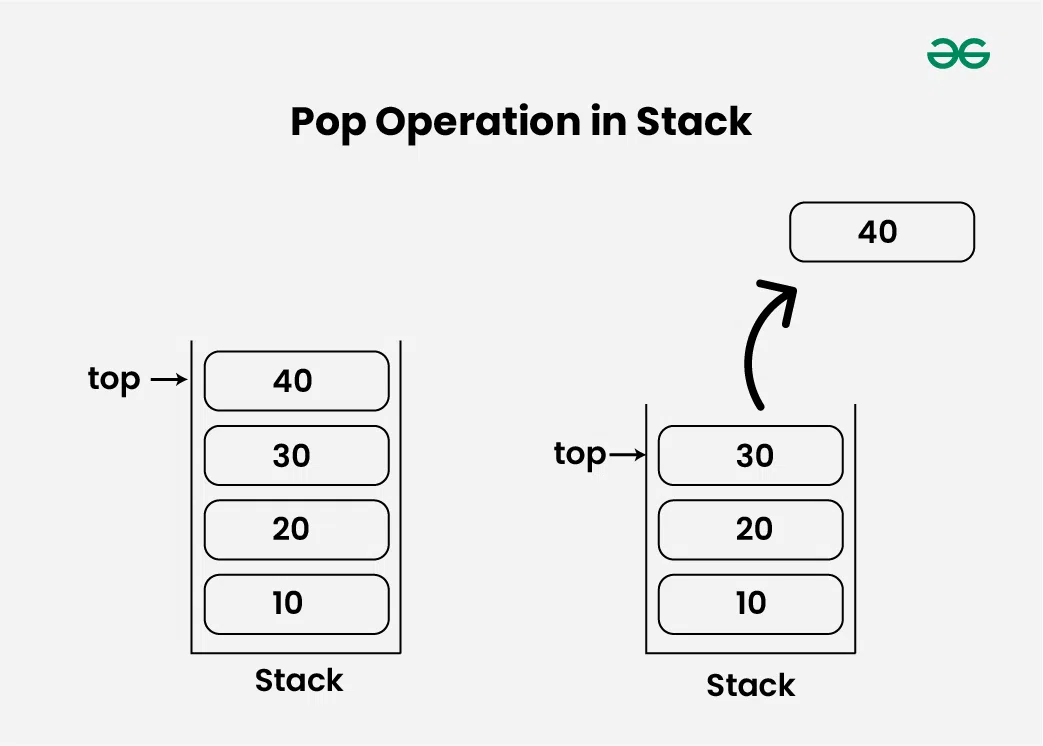
Pop Operation in Stack Data Structure:
Removes an item from the stack. The items are popped in the reversed order in which they are pushed. If the stack is empty, then it is said to be an Underflow condition.
Algorithm for Pop Operation:
- Before popping the element from the stack, we check if the stack is empty .
- If the stack is empty (top == -1), then Stack Underflows and we cannot remove any element from the stack.
- Otherwise, we store the value at top, decrement the value of top by 1 (top = top – 1) and return the stored top value.
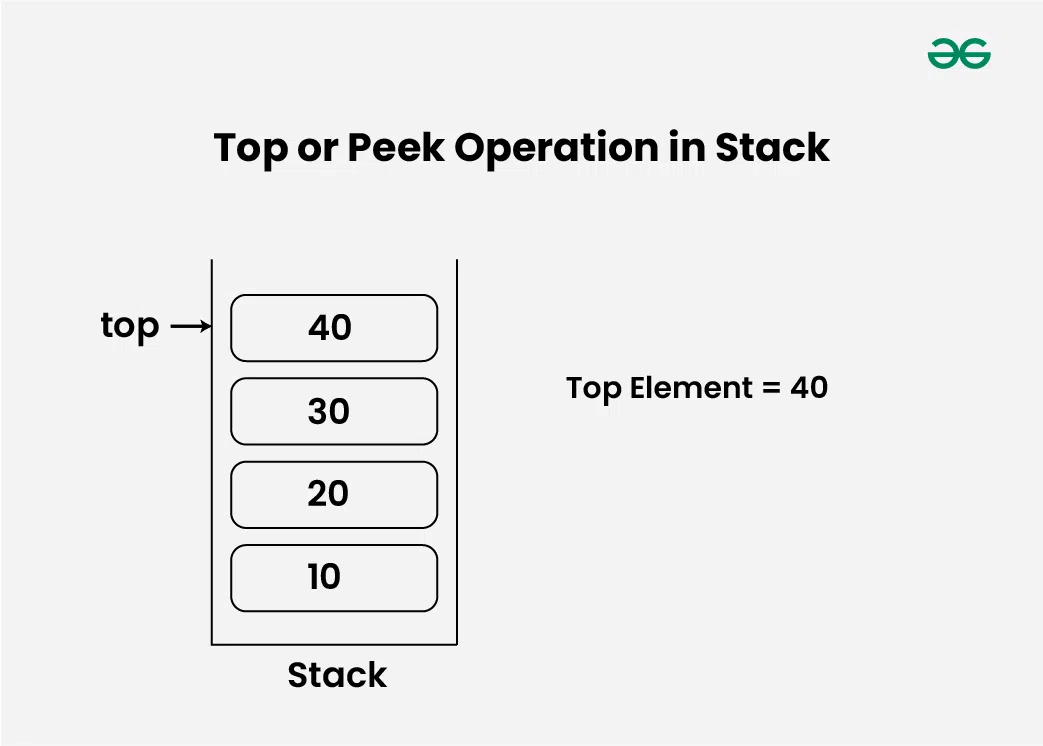
Top or Peek Operation in Stack Data Structure:
Returns the top element of the stack.
Algorithm for Top Operation:
- Before returning the top element from the stack, we check if the stack is empty.
- If the stack is empty (top == -1), we simply print “Stack is empty”.
- Otherwise, we return the element stored at index = top .
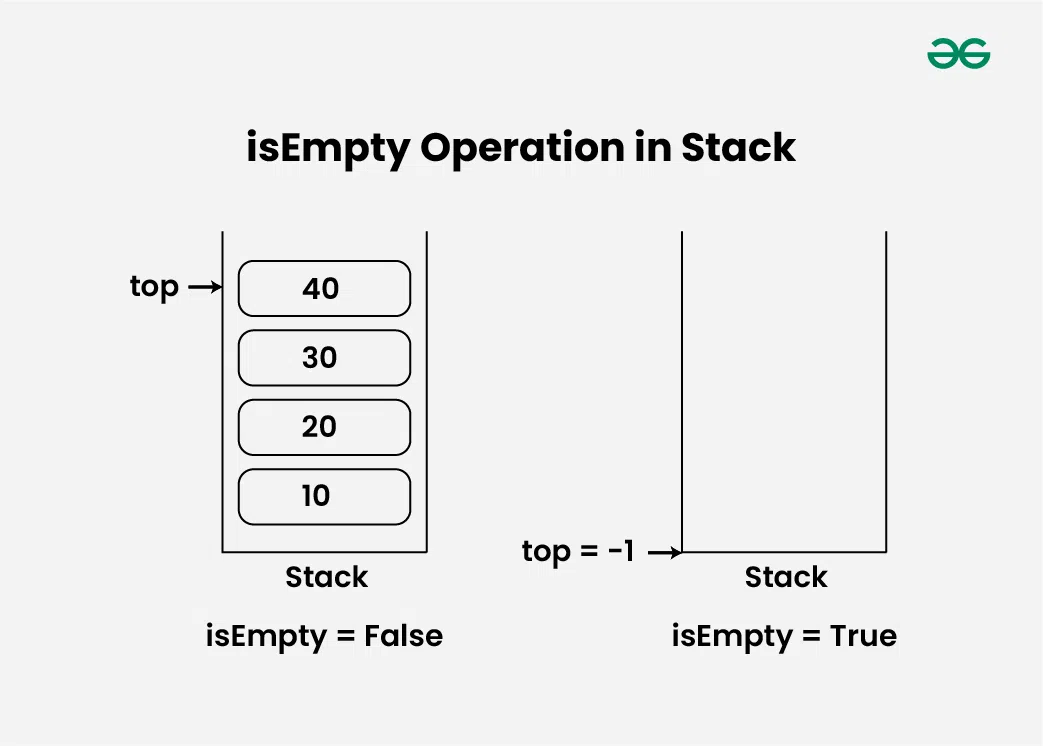
isEmpty Operation in Stack Data Structure:
Returns true if the stack is empty, else false.
Algorithm for isEmpty Operation:
- Check for the value of top in stack.
- If (top == -1) , then the stack is empty so return true .
- Otherwise, the stack is not empty so return false .
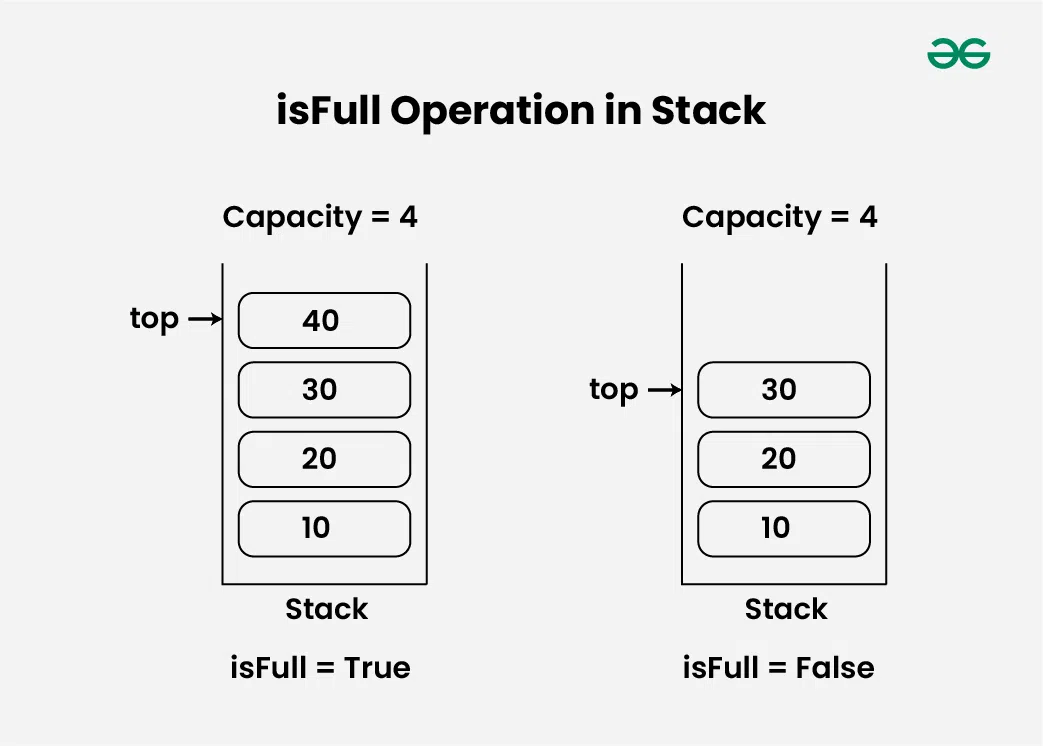
isFull Operation in Stack Data Structure:
Returns true if the stack is full, else false.
Algorithm for isFull Operation:
- Check for the value of top in stack.
- If (top == capacity-1), then the stack is full so return true.
- Otherwise, the stack is not full so return false.
Implementation of Stack Data Structure:
The basic operations that can be performed on a stack include push, pop, and peek. There are two ways to implement a stack –
- Using Array
- Using Linked List
In an array-based implementation, the push operation is implemented by incrementing the index of the top element and storing the new element at that index. The pop operation is implemented by returning the value stored at the top index and then decrementing the index of the top element.
In a linked list-based implementation, the push operation is implemented by creating a new node with the new element and setting the next pointer of the current top node to the new node. The pop operation is implemented by setting the next pointer of the current top node to the next node and returning the value of the current top node.
Implementation of Stack Data Structure using Array:
C++
/* C++ program to implement basic stack
operations */
#include <bits/stdc++.h>
#include<iostream>
using namespace std;
#define MAX 1000
class Stack {
int top;
public:
int a[MAX]; // Maximum size of Stack
Stack() { top = -1; }
bool push(int x);
int pop();
int peek();
bool isEmpty();
};
bool Stack::push(int x)
{
if (top >= (MAX - 1)) {
cout << "Stack Overflow";
return false;
}
else {
a[++top] = x;
cout << x << " pushed into stack\n";
return true;
}
}
int Stack::pop()
{
if (top < 0) {
cout << "Stack Underflow";
return 0;
}
else {
int x = a[top--];
return x;
}
}
int Stack::peek()
{
if (top < 0) {
cout << "Stack is Empty";
return 0;
}
else {
int x = a[top];
return x;
}
}
bool Stack::isEmpty()
{
return (top < 0);
}
// Driver program to test above functions
int main()
{
class Stack s;
s.push(10);
s.push(20);
s.push(30);
cout << s.pop() << " Popped from stack\n";
//print top element of stack after popping
cout << "Top element is : " << s.peek() << endl;
//print all elements in stack :
cout <<"Elements present in stack : ";
while(!s.isEmpty())
{
// print top element in stack
cout << s.peek() <<" ";
// remove top element in stack
s.pop();
}
return 0;
}
//Code is Modified By Vinay Pandey
// C program for array implementation of stack
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a stack
struct Stack {
int top;
unsigned capacity;
int* array;
};
// function to create a stack of given capacity. It initializes size of
// stack as 0
struct Stack* createStack(unsigned capacity)
{
struct Stack* stack = (struct Stack*)malloc(sizeof(struct Stack));
stack->capacity = capacity;
stack->top = -1;
stack->array = (int*)malloc(stack->capacity * sizeof(int));
return stack;
}
// Stack is full when top is equal to the last index
int isFull(struct Stack* stack)
{
return stack->top == stack->capacity - 1;
}
// Stack is empty when top is equal to -1
int isEmpty(struct Stack* stack)
{
return stack->top == -1;
}
// Function to add an item to stack. It increases top by 1
void push(struct Stack* stack, int item)
{
if (isFull(stack))
return;
stack->array[++stack->top] = item;
printf("%d pushed to stack\n", item);
}
// Function to remove an item from stack. It decreases top by 1
int pop(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack->array[stack->top--];
}
// Function to return the top from stack without removing it
int peek(struct Stack* stack)
{
if (isEmpty(stack))
return INT_MIN;
return stack->array[stack->top];
}
// Driver program to test above functions
int main()
{
struct Stack* stack = createStack(100);
push(stack, 10);
push(stack, 20);
push(stack, 30);
printf("%d popped from stack\n", pop(stack));
return 0;
}
/* Java program to implement basic stack
operations */
class Stack {
static final int MAX = 1000;
int top;
int a[] = new int[MAX]; // Maximum size of Stack
boolean isEmpty()
{
return (top < 0);
}
Stack()
{
top = -1;
}
boolean push(int x)
{
if (top >= (MAX - 1)) {
System.out.println("Stack Overflow");
return false;
}
else {
a[++top] = x;
System.out.println(x + " pushed into stack");
return true;
}
}
int pop()
{
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int x = a[top--];
return x;
}
}
int peek()
{
if (top < 0) {
System.out.println("Stack Underflow");
return 0;
}
else {
int x = a[top];
return x;
}
}
void print(){
for(int i = top;i>-1;i--){
System.out.print(" "+ a[i]);
}
}
}
// Driver code
class Main {
public static void main(String args[])
{
Stack s = new Stack();
s.push(10);
s.push(20);
s.push(30);
System.out.println(s.pop() + " Popped from stack");
System.out.println("Top element is :" + s.peek());
System.out.print("Elements present in stack :");
s.print();
}
}
//This code is Modified by Vinay Pandey
# Python program for implementation of stack
# import maxsize from sys module
# Used to return -infinite when stack is empty
from sys import maxsize
# Function to create a stack. It initializes size of stack as 0
def createStack():
stack = []
return stack
# Stack is empty when stack size is 0
def isEmpty(stack):
return len(stack) == 0
# Function to add an item to stack. It increases size by 1
def push(stack, item):
stack.append(item)
print(item + " pushed to stack ")
# Function to remove an item from stack. It decreases size by 1
def pop(stack):
if (isEmpty(stack)):
return str(-maxsize -1) # return minus infinite
return stack.pop()
# Function to return the top from stack without removing it
def peek(stack):
if (isEmpty(stack)):
return str(-maxsize -1) # return minus infinite
return stack[len(stack) - 1]
# Driver program to test above functions
stack = createStack()
push(stack, str(10))
push(stack, str(20))
push(stack, str(30))
print(pop(stack) + " popped from stack")
// C# program to implement basic stack
// operations
using System;
namespace ImplementStack {
class Stack {
private int[] ele;
private int top;
private int max;
public Stack(int size)
{
ele = new int[size]; // Maximum size of Stack
top = -1;
max = size;
}
public void push(int item)
{
if (top == max - 1) {
Console.WriteLine("Stack Overflow");
return;
}
else {
ele[++top] = item;
}
}
public int pop()
{
if (top == -1) {
Console.WriteLine("Stack is Empty");
return -1;
}
else {
Console.WriteLine("{0} popped from stack ",
ele[top]);
return ele[top--];
}
}
public int peek()
{
if (top == -1) {
Console.WriteLine("Stack is Empty");
return -1;
}
else {
Console.WriteLine("{0} popped from stack ",
ele[top]);
return ele[top];
}
}
public void printStack()
{
if (top == -1) {
Console.WriteLine("Stack is Empty");
return;
}
else {
for (int i = 0; i <= top; i++) {
Console.WriteLine("{0} pushed into stack",
ele[i]);
}
}
}
}
// Driver program to test above functions
class Program {
static void Main()
{
Stack p = new Stack(5);
p.push(10);
p.push(20);
p.push(30);
p.printStack();
p.pop();
}
}
}
/* javascript program to implement basic stack
operations
*/
var t = -1;
var MAX = 1000;
var a = Array(MAX).fill(0); // Maximum size of Stack
function isEmpty() {
return (t < 0);
}
function push(x) {
if (t >= (MAX - 1)) {
console.log("Stack Overflow");
return false;
} else {
t+=1;
a[t] = x;
console.log(x + " pushed into stack<br/>");
return true;
}
}
function pop() {
if (t < 0) {
console.log("Stack Underflow");
return 0;
} else {
var x = a[t];
t-=1;
return x;
}
}
function peek() {
if (t < 0) {
console.log("Stack Underflow");
return 0;
} else {
var x = a[t];
return x;
}
}
function print() {
for (i = t; i > -1; i--) {
console.log(" " + a[i]);
}
}
push(10);
push(20);
push(30);
console.log(pop() + " Popped from stack");
console.log("<br/>Top element is :" + peek());
console.log("<br/>Elements present in stack : ");
print();
// This code is contributed by Rajput-Ji
Output10 pushed into stack
20 pushed into stack
30 pushed into stack
30 Popped from stack
Top element is : 20
Elements present in stack : 20 10
Advantages of Array Implementation:
- Easy to implement.
- Memory is saved as pointers are not involved.
Disadvantages of Array Implementation:
- It is not dynamic i.e., it doesn’t grow and shrink depending on needs at runtime. [But in case of dynamic sized arrays like vector in C++, list in Python, ArrayList in Java, stacks can grow and shrink with array implementation as well].
- The total size of the stack must be defined beforehand.
Implementation of Stack Data Structure using Linked List:
C++
// C++ program for linked list implementation of stack
#include <bits/stdc++.h>
using namespace std;
// A structure to represent a stack
class StackNode {
public:
int data;
StackNode* next;
};
StackNode* newNode(int data)
{
StackNode* stackNode = new StackNode();
stackNode->data = data;
stackNode->next = NULL;
return stackNode;
}
int isEmpty(StackNode* root)
{
return !root;
}
void push(StackNode** root, int data)
{
StackNode* stackNode = newNode(data);
stackNode->next = *root;
*root = stackNode;
cout << data << " pushed to stack\n";
}
int pop(StackNode** root)
{
if (isEmpty(*root))
return INT_MIN;
StackNode* temp = *root;
*root = (*root)->next;
int popped = temp->data;
free(temp);
return popped;
}
int peek(StackNode* root)
{
if (isEmpty(root))
return INT_MIN;
return root->data;
}
// Driver code
int main()
{
StackNode* root = NULL;
push(&root, 10);
push(&root, 20);
push(&root, 30);
cout << pop(&root) << " popped from stack\n";
cout << "Top element is " << peek(root) << endl;
cout <<"Elements present in stack : ";
//print all elements in stack :
while(!isEmpty(root))
{
// print top element in stack
cout << peek(root) <<" ";
// remove top element in stack
pop(&root);
}
return 0;
}
// This is code is contributed by rathbhupendra
// C program for linked list implementation of stack
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a stack
struct StackNode {
int data;
struct StackNode* next;
};
struct StackNode* newNode(int data)
{
struct StackNode* stackNode =
(struct StackNode*)
malloc(sizeof(struct StackNode));
stackNode->data = data;
stackNode->next = NULL;
return stackNode;
}
int isEmpty(struct StackNode* root)
{
return !root;
}
void push(struct StackNode** root, int data)
{
struct StackNode* stackNode = newNode(data);
stackNode->next = *root;
*root = stackNode;
printf("%d pushed to stack\n", data);
}
int pop(struct StackNode** root)
{
if (isEmpty(*root))
return INT_MIN;
struct StackNode* temp = *root;
*root = (*root)->next;
int popped = temp->data;
free(temp);
return popped;
}
int peek(struct StackNode* root)
{
if (isEmpty(root))
return INT_MIN;
return root->data;
}
int main()
{
struct StackNode* root = NULL;
push(&root, 10);
push(&root, 20);
push(&root, 30);
printf("%d popped from stack\n", pop(&root));
printf("Top element is %d\n", peek(root));
return 0;
}
// Java Code for Linked List Implementation
public class StackAsLinkedList {
StackNode root;
static class StackNode {
int data;
StackNode next;
StackNode(int data) { this.data = data; }
}
public boolean isEmpty()
{
if (root == null) {
return true;
}
else
return false;
}
public void push(int data)
{
StackNode newNode = new StackNode(data);
if (root == null) {
root = newNode;
}
else {
StackNode temp = root;
root = newNode;
newNode.next = temp;
}
System.out.println(data + " pushed to stack");
}
public int pop()
{
int popped = Integer.MIN_VALUE;
if (root == null) {
System.out.println("Stack is Empty");
}
else {
popped = root.data;
root = root.next;
}
return popped;
}
public int peek()
{
if (root == null) {
System.out.println("Stack is empty");
return Integer.MIN_VALUE;
}
else {
return root.data;
}
}
// Driver code
public static void main(String[] args)
{
StackAsLinkedList sll = new StackAsLinkedList();
sll.push(10);
sll.push(20);
sll.push(30);
System.out.println(sll.pop()
+ " popped from stack");
System.out.println("Top element is " + sll.peek());
sll.push(10);
sll.push(20);
sll.push(30);
System.out.println(sll.pop()
+ " popped from stack");
System.out.println("Top element is " + sll.peek());
}
}
# Python program for linked list implementation of stack
# Class to represent a node
class StackNode:
# Constructor to initialize a node
def __init__(self, data):
self.data = data
self.next = None
class Stack:
# Constructor to initialize the root of linked list
def __init__(self):
self.root = None
def isEmpty(self):
return True if self.root is None else False
def push(self, data):
newNode = StackNode(data)
newNode.next = self.root
self.root = newNode
print ("% d pushed to stack" % (data))
def pop(self):
if (self.isEmpty()):
return float("-inf")
temp = self.root
self.root = self.root.next
popped = temp.data
return popped
def peek(self):
if self.isEmpty():
return float("-inf")
return self.root.data
# Driver code
stack = Stack()
stack.push(10)
stack.push(20)
stack.push(30)
print ("% d popped from stack" % (stack.pop()))
print ("Top element is % d " % (stack.peek()))
# This code is contributed by Nikhil Kumar Singh(nickzuck_007)
// C# Code for Linked List Implementation
using System;
public class StackAsLinkedList {
StackNode root;
public class StackNode {
public int data;
public StackNode next;
public StackNode(int data) { this.data = data; }
}
public bool isEmpty()
{
if (root == null) {
return true;
}
else
return false;
}
public void push(int data)
{
StackNode newNode = new StackNode(data);
if (root == null) {
root = newNode;
}
else {
StackNode temp = root;
root = newNode;
newNode.next = temp;
}
Console.WriteLine(data + " pushed to stack");
}
public int pop()
{
int popped = int.MinValue;
if (root == null) {
Console.WriteLine("Stack is Empty");
}
else {
popped = root.data;
root = root.next;
}
return popped;
}
public int peek()
{
if (root == null) {
Console.WriteLine("Stack is empty");
return int.MinValue;
}
else {
return root.data;
}
}
// Driver code
public static void Main(String[] args)
{
StackAsLinkedList sll = new StackAsLinkedList();
sll.push(10);
sll.push(20);
sll.push(30);
Console.WriteLine(sll.pop() + " popped from stack");
Console.WriteLine("Top element is " + sll.peek());
}
}
/* This code contributed by PrinciRaj1992 */
<script>
// javascript Code for Linked List Implementation
var root;
class StackNode {
constructor(data) {
this.data = data;
this.next = null;
}
}
function isEmpty() {
if (root == null) {
return true;
} else
return false;
}
function push(data) {
var newNode = new StackNode(data);
if (root == null) {
root = newNode;
} else {
var temp = root;
root = newNode;
newNode.next = temp;
}
document.write(data + " pushed to stack<br/>");
}
function pop() {
var popped = Number.MIN_VALUE;
if (root == null) {
document.write("Stack is Empty");
} else {
popped = root.data;
root = root.next;
}
return popped;
}
function peek() {
if (root == null) {
document.write("Stack is empty");
return Number.MIN_VALUE;
} else {
return root.data;
}
}
// Driver code
push(10);
push(20);
push(30);
document.write(pop() + " popped from stack<br/>");
document.write("Top element is " + peek());
// This code is contributed by Rajput-Ji
</script>
Output10 pushed to stack
20 pushed to stack
30 pushed to stack
30 popped from stack
Top element is 20
Elements present in stack : 20 10
Advantages of Linked List implementation:
- The linked list implementation of a stack can grow and shrink according to the needs at runtime.
- It is used in many virtual machines like JVM.
Disadvantages of Linked List implementation:
- Requires extra memory due to the involvement of pointers.
- Random accessing is not possible in stack.
Complexity Analysis of Operations on Stack Data Structure:
| Operations | Time Complexity | Space Complexity
|
|---|
| push() | O(1) | O(1)
|
|---|
| pop() | O(1) | O(1)
|
|---|
top() or peek()
| O(1)
| O(1)
|
|---|
| isEmpty() | O(1) | O(1)
|
|---|
| isFull() | O(1) | O(1)
|
|---|
Advantages of Stack Data Structure:
- Simplicity: Stacks are a simple and easy-to-understand data structure, making them suitable for a wide range of applications.
- Efficiency: Push and pop operations on a stack can be performed in constant time (O(1)) , providing efficient access to data.
- Last-in, First-out (LIFO): Stacks follow the LIFO principle, ensuring that the last element added to the stack is the first one removed. This behavior is useful in many scenarios, such as function calls and expression evaluation.
- Limited memory usage: Stacks only need to store the elements that have been pushed onto them, making them memory-efficient compared to other data structures.
Disadvantages of Stack Data Structure:
- Limited access: Elements in a stack can only be accessed from the top, making it difficult to retrieve or modify elements in the middle of the stack.
- Potential for overflow: If more elements are pushed onto a stack than it can hold, an overflow error will occur, resulting in a loss of data.
- Not suitable for random access: Stack s do not allow for random access to elements, making them unsuitable for applications where elements need to be accessed in a specific order.
- Limited capacity: Stacks have a fixed capacity, which can be a limitation if the number of elements that need to be stored is unknown or highly variable.
Applications of Stack Data Structure:
- Infix to Postfix /Prefix conversion
- Redo-undo features at many places like editors, photoshop.
- Forward and backward features in web browsers
- In Memory management, any modern computer uses a stack as the primary management for a running purpose. Each program that is running in a computer system has its own memory allocations.
- Stack also helps in implementing function call in computers. The last called function is always completed first.
Related Articles: