Grafisk fremstilling av en Boltzmann-maskin. Maskinen består av et nettverk av enheter som henger sammen på en liknende måte som nerveceller. Disse enhetene er representert med de grå sirklene og kalles s1, s2, og så videre. Enhetene kan ta verdiene 0 eller 1. I figuren er det syv av disse enhetene. Alle enhetene kan kommunisere med hverandre via strekene. Koblingsstyrken mellom enhetene er representert med variablene w. Koblingen mellom for eksempel enhet s1 og s2 er w12. I tillegg vil verdien som enhetene har påvirkes av parametrene θ. Ved å justere verdien på koblingsstyrkene w og parametrene θ, kan man få nettverket til å utføre bestemte oppgaver når det mottar et signal. Signalet inngår i nettverket ved at det låser verdien til en eller flere av enhetene (grå sirkler).
En Boltzmann-maskin er i fagområdet kunstig intelligens et nettverk som består av enheter som henger sammen på en måte som minner om nerveceller. Nettverket kan utføre oppgaver innenfor blant annet maskinlæring. Boltzmann-maskinen har spilt en viktig rolle i utviklingen av nye typer nevrale nettverk.
Boltzmann-maskinen ble funnet opp av Geoffrey E. Hinton (født 1947). Navnet kommer fra fysikeren Ludwig Boltzmann.
I 2024 fikk Geoffrey E. Hinton, sammen med John J. Hopfield (født 1933), nobelprisen i fysikk for deres bidrag til kunstig intelligens gjennom utviklingen av Boltzmann-maskinen og Hopfield-nettverket.
I menneskehjernen finnes det et nettverk av nerveceller som er koblet sammen og kan sende signaler til hverandre. Måten nervecellene kommuniserer på er å danne koblinger mellom seg.
I kunstig intelligens er den grunnleggende idéen at man skal bruke et kunstig fremstilt nettverk av enheter som minner om nervecellenes nettverk. Dette kalles et nevralt nettverk. Målet er å utføre oppgaver som menneskehjernen er god på, men raskere eller bedre enn menneskehjernen klarer. Eksempler på slike oppgaver er bildegjenkjenning og klassifisering.
For at nettverket skal kunne utføre bestemte oppgaver, slik som bildegjenkjenning, må nettverket først bli trent på et sett med data. Dette kan for eksempel være at nettverket mottar et bilde av en hest og at det gjenkjenner dette som et dyr i stedet for et menneske. Resultatet nettverket produserer blir da «dette er et dyr».
Den generelle Boltzmann-maskinen har spilt en viktig rolle i utviklingen av nye typer nevrale nettverk innen kunstig intelligens.
I praksis er Boltzmann-maskinen ikke så effektiv til å lære seg nye oppgaver. Derimot kan en justering av modellen til en såkalt begrenset Boltzmann-maskin gjøre nettverket mye mer effektivt til å lære seg oppgaver, slik som gjenkjennelse av tale.
Noen nevrale nettverk kan beskrives matematisk av en Hamilton-funksjon. Denne funksjonen er en modell for energien \( E \) til systemet. Boltzmann-maskinen er et nettverk som matematisk beskrives av en såkalt Sherrington-Kirkpatrick modell:
\[E = -(\sum_{i<j} w_{ij} s_i s_j + \sum_i \theta_i s_i)\]
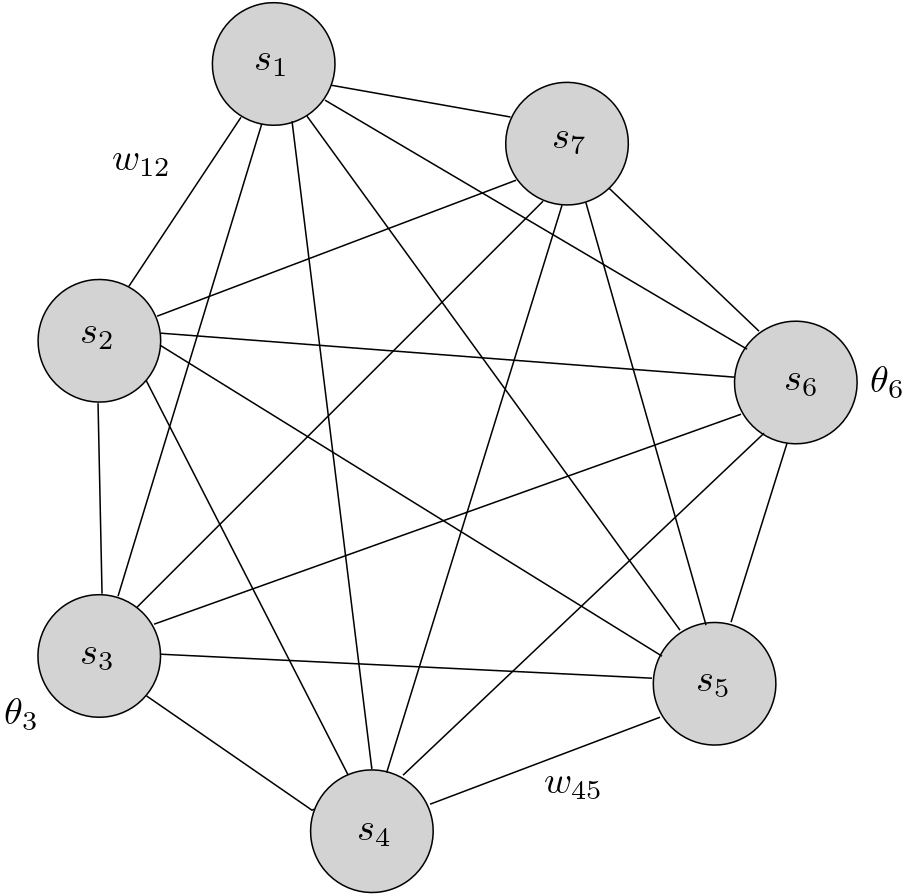
I denne modellen er de enkelte enhetene beskrevet av variablene \( s_i \) som er koblet sammen med en styrke \( w_{ij} \). Variablene \( s_i \) kan kun ha verdien 0 eller 1. Størrelsen \( \theta_i \) angir energien knyttet til hver enkelt variabel \( s_i \), uavhengig av hvordan den kobler til andre enheter. Energien er en summering av alle variablene \( s_i \) og koblingen mellom dem.
Den matematiske modellen for energien \( E \) beskriver rent fysisk et såkalt spinn-glass materiale som befinner seg i et ytre magnetisk felt.
For å trene nettverket endrer man koblingsstyrkene \( w_{ij} \) helt til nettverket kan motta et signal og produsere et nytt, riktig, signal.
Kommentarer
Kommentarer til artikkelen blir synlig for alle. Ikke skriv inn sensitive opplysninger, for eksempel helseopplysninger. Fagansvarlig eller redaktør svarer når de kan. Det kan ta tid før du får svar.
Du må være logget inn for å kommentere.