Interferenca

Interferénca je pojav, ko se dve koherentni valovanji srečata na istem mestu in nastane nov valovni vzorec. Skupni odmik nihajoče količine (npr. odmik, jakost električnega polja) je enak vsoti odmikov te količine posameznih valovanj. Kjer se valovni hrbti prvega valovanja ujemajo z valovnimi hrbti drugega valovanja, se skupna amplituda poveča. Reče se, da tam pride do konstruktivne interference. Na mestu, kjer sta valovanji v protifazi, pride valovni hrbet prvega valovanja na valovno dolino drugega valovanja in na tem mestu se valovanji vzajemno oslabita. Pojav se imenuje destruktivna interferenca.

Interferenca dveh nasprotno potujočih valovanj (zelena in modra) v eni razsežnosti ter novonastali val (rdeča)

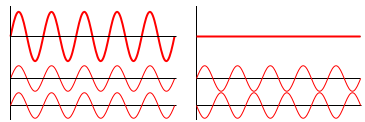
Seštevek valovanj
Valovanje 1
Valovanje 2
	Konstruktivna interferenca	Destruktivna interferenca

Interferenco se opazi pri vseh vrstah koherentnega valovanja, pri svetlobnem, radijskem, zvočnem in vodnem valovanju. Da bosta dve valovanji interferirali, morata imeti enako valovno dolžino in fazo.

Optična interferenca

Interferenca dveh krogelnih valovanj

Interferenčni pojav pri svetlobi je težko opazovati zaradi kratke valovne dolžine (vidna svetloba ima valovno dolžino 400 - 700 nm).

Prvi je pojav optične interference pokazal Thomas Young leta 1801. Pokazal je, da svetloba, ki vpade na dve vzporedni reži, interferira. Na zaslonu tako nastane vzorec, sestavljen iz ojačitev in oslabitev. Sicer pa navadno za doseganje koherentnega izvora svetlobe uporabimo laser, ki ima točno določeno valovno dolžino in polarizacijo. Svetlobni curek usmerimo na reži, ki služita kot razdelilnik. Pred izumom laserja so uporabljali svetilke z natrijevimi ali živosrebrnimi parami, saj so za ta elementa značilne ozke spektralne črte, ki prav tako omogočajo interferenco.

Matematični opis

Nadaljnja izpeljava velja za superpozicijo odmikov splošne količine, v našem primeru za električno polje z jakostjo ${\vec {E}}$.

Svetloba je elektromagnetno valovanje. Opišemo jo z vektorskim poljem, zato moramo tudi amplitude nihanj obravnavati vektorsko. Električno polje ${\vec {E}}$ na neki točki v prostoru je torej vektorski seštevek posameznih prispevajočih polj ${\vec {E}}={\vec {E_{1}}}+{\vec {E_{2}}}...$ Električno polje svetlobe se zelo hitro spreminja, zato njegovega spreminjanja ne moremo zaznati. Lahko pa opazujemo gostoto svetlobnega toka $j$, ki jo v praznem prostoru zapišemo kot

$j=\epsilon _{0}c_{0}\langle \vert {\vec {E}}\vert ^{2}\rangle ,$

kjer je

• $\epsilon _{0}$ influenčna konstanta in
• $c_{0}$ hitrost svetlobe.

To pomeni, da je jakost $j$ sorazmerna s časovnim povprečjem kvadrata električnega polja.

Predpostavimo, da imamo dva vira, iz katerih izhaja linearno polarizirana svetloba oblike:

${\vec {E}}_{1}({\vec {r}},t)={\vec {E}}_{01}\cos({\vec {k}}_{1}{\vec {r}}-\omega t+\delta _{1})$

in

${\vec {E}}_{2}({\vec {r}},t)={\vec {E}}_{02}\cos({\vec {k}}_{2}{\vec {r}}-\omega t+\delta _{2}),$

kjer sta

• ${\vec {k}}_{1},{\vec {k}}_{2}$ valovna vektorja pripadajočih valovanj,
• $\delta _{1},\delta _{2}$ pa fazna zamika valovanj.

Kvadrat seštevka polj ${\vec {E}}_{1}$ in ${\vec {E}}_{2}$ je:

$E^{2}={\vec {E}}\cdot {\vec {E}}=$

$=\left({\vec {E}}_{1}+{\vec {E}}_{2}\right)\cdot \left({\vec {E}}_{1}+{\vec {E}}_{2}\right)=$

$=E_{1}^{2}+2{\vec {E}}_{1}\cdot {\vec {E}}_{2}+E_{2}^{2}.$

Gostota svetlobnega toka je

$j=j_{1}+j_{2}+j_{12},$

kjer je

• $j_{1}\propto E_{1}^{2}$ in predstavlja prispevek prvega izvora; podobno $j_{2}$,
• $j_{12}$ pa je interferenčni člen oblike

$j_{12}=\epsilon _{0}c_{0}\langle {\vec {E}}_{1}\cdot {\vec {E}}_{2}\rangle .$

Če interferenčni člen izpišemo in upoštevamo sinusno naravo valovanja (časovno povprečje $\langle \sin ^{2}\omega t\rangle ={\frac {1}{2}}$ in $\langle \sin \omega t\cos \omega t\rangle =0$), dobimo

$j_{12}=\epsilon _{0}c_{0}{\vec {E}}_{01}\cdot {\vec {E}}_{02}\cos \delta ,$

kjer je:

• $\delta =\delta _{1}-\delta _{2}$ razlika faz interferirajočih valovanj.

Celotna gostota svetlobnega toka se tako ponekod ojača, drugod pa oslabi. V primeru, da imata vpadni valovanji enako amplitudo, je na mestih oslabitve gostota toka enaka nič, na mestih ojačitve pa štirikrat večja od toka posameznega vpadnega valovanja.

Interferenca na dveh tankih režah

Interferenca ravnega valovanja na dveh režah ter nastala slika na zaslonu z vidnimi maksimumi in minimumi

Obravnavajmo dve tanki reži na razalji $d$, na kateri vpada valovanje. Za zgled zopet vzemimo svetlobo, to je elektromagnetno valovanje z električno poljsko jakostjo ${\vec {E}}$ (čeprav velja tudi za druga valovanja, na primer na vodni gladini). Na reži posvetimo s koherentno svetlobo z amplitudo električne poljske jakosti $E_{0}$. Naj bo oddaljenost zaslona od rež velika, $\vert {\vec {r}}\vert \gg d$, kar pomeni, da imata žarka iz obeh rež približno enako smer. Izhodišče koordinatnega sistema postavimo na eno izmed rež tako, da je valovni vektor ${\vec {k}}$ vzporeden z ${\vec {r}}$ in velja ${\vec {k}}\cdot {\vec {r}}=kr$. Nastavka valovanj iz obeh rež (naj bosta enako polarizirani) sta:

$E_{1}=E_{0}\mathrm {e} ^{i(kr-\omega t)}$

$E_{2}=E_{0}\mathrm {e} ^{i(k(r+\Delta r)-\omega t)},$

kjer je:

• $\omega$ krožna frekvenca svetlobe,
• $\Delta r$ pa razlika poti, ki jo drugi žarek opravi glede na prvega, ker izhaja iz druge reže.

Skupno električno polje je seštevek obeh prispevkov, $E=E_{1}+E_{2}$:

$E=E_{0}\mathrm {e} ^{i(kr-\omega t)}\left(1+\mathrm {e} ^{ik\Delta r}\right)=2E_{0}\mathrm {e} ^{i(k(r+\Delta r/2)-\omega t)}\cos {\frac {k\Delta r}{2}}.$

Razliko poti se izrazi s kotom:

Geometrija žarkov za velike oddaljenosti od rež. Na sliki je vidna razlika poti žarkov.

$\Delta r=d\sin \theta ,$

upoštevamo se, da je vpadna jakost svetlobe enaka:

$j_{0}={\frac {1}{2}}\epsilon _{0}c_{0}\vert E\vert ^{2},$

in se dobi:

$j(\theta )=4j_{0}\cos ^{2}\left({\frac {\pi d\sin \theta }{\lambda }}\right).$

Največja ojačitev (konstruktivna interferenca) nastopi pri tistih kotih $\theta _{max}$, pri katerih je razlika poti žarkov enaka večkratniku valovne dolžine $\lambda$. Ničelno intenziteto (destruktivno interferenco) pa dobimo pri tistih kotih $\theta _{min}$, pri katerih se poti razlikujeta za polovico (in še poljuben celoštevilski večkratnik $N$) valovne dolžine $\lambda$:

$d\sin \theta _{max}=N\lambda ,$

$d\sin \theta _{min}=(N+{\frac {1}{2}})\lambda .$

Interferenca na več tankih režah

Interferenca laserske svetlobe na dveh (zgoraj) in na petih režah (spodaj). Razdalje med režami na uklonski mrežici so enake. S povečevanjem števila rež postaja interferenčni vzorec vse ostrejši.

Če valovanje z gostoto svetlobenga toka $j_{0}$ vpade na zaslon z $N$ režami, je intenziteta po prehodu

$j(\delta )=j_{0}{\frac {\sin ^{2}N\delta }{\sin ^{2}\delta }},$

kjer je:

• $\delta ={\frac {\pi d\sin \theta }{\lambda }}.$

Pogoj za konstruktivno in destruktivno interferenco je enak kot pri dveh režah, z višanjem števila rež pa se interferenčni vrhovi ožijo in višajo.

Interferenca na tankih plasteh

Interferenca bele svetlobe na milnem mehurčku.

Interferenčni pojav se opazi na tankih plasteh, kot na primer na tanki plasti olja na vodi ali milnih mehurčkih. Raznobarvni vzorci se pojavijo zaradi interference med odbitimi valovanji z nasprotnih strani tanke plasti. Pri določeni debelini tanke plasti se ojača samo določena barva, zato se vzorec s spremenljivo debelino vidi mavrično obarvan.

Konstruktivna interferenca na tanki plasti

Destruktivna interferenca na tanki plasti

Interferenca na kristalih

Podobno kot za interferenco na tankih plasteh velja tudi za interferenčne vzorce na kristalnih mrežah, saj si ravnine v kristalni mreži lahko predstavljamo kot tanke plasti. Pri tem mora biti za ojačitev zadoščeno Braggovemu oziroma Lauejevemu pogoju za konstruktivno interferenco (pogoja sta enakovredna). Braggov pogoj se glasi:

$2d\sin \theta =m\lambda ,$

kjer so:

• $d$ razdalja med ravninami v kristalni mreži,
• $\theta$ vpadni kot svetlobe,
• $m$ poljubno celo število in
• $\lambda$ valovna dolžina svetlobe.

Lauejev pogoj se glasi:

${\vec {k}}\cdot {\hat {K}}={\frac {K}{2}},$

kjer sta:

• ${\vec {k}}$ valovni vektor svetlobe in
• ${\vec {K}}$ vektor recipročne rešetke Bravaisove mreže.

Uporaba

Optična interferometrija

Michelsonov interferometer, s katerim je bil izveden Michelson–Morleyjev poskus

Leta 1801 je Young z uporabo dvojne reže dosegel interferenco. To je služilo kot močan dokaz v prid valovne narave svetlobe. Z interferenco je Young izmeril tudi valovne dolžine različnih barv vidnega spektra.

Na podlagi rezultatov Michelson-Morleyjevega poskusa, ki za svoje delovanje uporablja interferenco dveh laserskih snopov, so ovrgli obstoj etra in potrdili Einsteinovo splošno teorijo relativnosti.

Interferenca je služila tudi pri definiciji in kalibraciji dolžinskih standardov. Leta 1960 je bil meter v novem SI sistemu definiran kot 1 650 763,73 valovnih dolžin oranžno-rdeče emisijske črte v elektromagnetnem spektru kriptona 86 v vakuumu. Leta 1983 so definicijo metra nadomestili z razdaljo, ki jo prepotuje svetloba v vakuumu v določenem časovnem intervalu.

Interferometrija se danes uporablja za točne meritve razdalj in določanje kristalnih struktur. Uporablja se tudi za testiranje optičnih komponent.

Radijska interferometrija

Niz posameznih teleskopov, ki skupaj tvorijo večji radijski teleskop

Radijska interferometrija se uporablja v astronomiji. Niz paraboličnih krožnikov ali anten postavijo na način, ki omogoči medsebojno interferenco signalov. S tem se signal ojača in izboljša ločljivost signala.

Akustična interferometrija

Akustični interferometer je inštrument za merjenje fizikalnih značilnosti zvočnih valovanj v plinu ali kapljevini. Uporablja se za merjenje hitrosti, valovne dolžine in absorpcije zvočnih valovanj.

Viri

• Michelson, Albert Abraham; Morley, Edward Williams (1887), »On the Relative Motion of the Earth and the Luminiferous Ether«, The American Journal of Science, 34 (203): 333–345