Quadratura del cerchio

La quadratura del cerchio, assieme al problema della trisezione dell'angolo e a quello della duplicazione del cubo, è un problema classico della matematica greca (più precisamente della geometria), il cui scopo è costruire un quadrato che abbia la stessa area di un dato cerchio, con uso esclusivo di riga e compasso.

Un cerchio e la sua "quadratura": le figure hanno uguale area

Storia e descrizione del problema

Oronzio Fineo, Quadratura circuli, 1544

J. P. de Fauré, Dissertation, découverte, et demonstrations de la quadrature mathematique du cercle, 1747

Il problema risale alle origini della geometria, e tenne occupati i matematici per secoli. Tra i numerosi studiosi del problema: Nicola Cusano nel 1450, Oronzio Fineo nel 1544, Vincent Léotaud nel 1654, Ottavio Scarlattini nel 1690, J. P. de Fauré nel 1740-47, Filippo Carmagnini nel 1751, Guillaume le Roberger de Vausenville nel 1774. Giovanni Battista Della Porta pubblicò nel 1610 a Roma l'opera intitolata: Elementorum curvilineorum libri tres. In quibus altera Geometriae parte restituta, agitur de Circuli Quadratura, dove egli tenta di quadrare il cerchio ricorrendo alle lunule. Questa quadratura fu poi confutata da Giovanni Camillo Glorioso nella Exercitationum mathematicarum Decas prima, Neapoli, 1627 alla Exercitatio IV (pp. 49-69).

Fu solo nel 1882 che l'impossibilità venne provata rigorosamente, anche se i matematici dell'antichità avevano compreso molto bene, sia intuitivamente che in pratica, la sua intrattabilità.

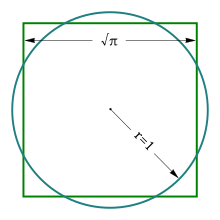
Trovare una soluzione richiederebbe la costruzione del numero ${\sqrt {\pi }}$ (infatti l'area del cerchio è $\pi r^{2}$, quindi un quadrato con area $\pi r^{2}$ deve avere lato pari a $r{\sqrt {\pi }}$). L'impossibilità di una tale costruzione, con le limitazioni imposte dall'uso esclusivo di riga e compasso, deriva dal fatto che π è un numero trascendente, ovvero non-algebrico, e quindi non-costruibile. La trascendenza di π fu dimostrata da Ferdinand von Lindemann nel 1882.

La soluzione del problema della quadratura del cerchio con riga e compasso implicherebbe quindi trovare anche un valore algebrico per π - il che si è dimostrato impossibile dopo il lavoro di Lindemann.

Ciò non implica invece che sia impossibile costruire un quadrato la cui area approssimi molto da vicino quella del cerchio dato. Ad esempio si può costruire un lato di $39/22=1,7727\ldots$, che è una buona approssimazione di ${\sqrt {\pi }}=1,7724\ldots$.

La "quadratura del cerchio" come metafora

Nel 1882 Ferdinand von Lindemann pubblicò la dimostrazione della trascendenza di pi greco. Precedentemente egli aveva già dimostrato che se pi greco fosse stato trascendente, allora l'antico problema della quadratura del cerchio con riga e compasso sarebbe stato irrisolvibile. Fino a quel momento erano stati innumerevoli i tentativi della quadratura matematica del cerchio, tanto che l'espressione era (ed è) diventata sinonimo di un'impresa vana, senza speranza o priva di un significato concreto.

In senso meramente letterario, l'espressione "quadratura del cerchio", viene spesso usata per indicare la soluzione perfetta a un dato problema (anche se, come abbiamo visto, non esiste).

Significato della quadratura del cerchio

«Qual è il geometra che tutto s'affige
per misurar lo cerchio, e non ritrova,
pensando, quel principio ond'elli indige,
tal era io a quella vista nova.»
(Dante, Paradiso, XXXIII, 133-136)

Quadratura alchemica del cerchio, simbolo geometrico della pietra filosofale.

La quadratura del cerchio non era un semplice rompicapo ludico, ma rispondeva ad esigenze di natura profondamente esoterica, assurgendo a simbolo della congiunzione alchemica degli opposti e della pietra filosofale: essendo il cerchio tradizionalmente associato al Cielo e il quadrato alla Terra, far coincidere matematicamente le due figure equivaleva a comporre lo Spirito con la Materia, il Trascendente con l'Immanente, realizzando il rebis o l'androgino in cui consisteva il segreto della creazione.

Conciliare il quadrato col cerchio significava in definitiva trovare la loro corrispondenza occulta, il catalizzatore in grado di risolvere ogni dualismo insanabile, scoprendo il senso dell'analogia enunciata nel motto ermetico «come in alto così in basso».

L'uomo vitruviano, simbolo dell'analogia tra il Cielo, rappresentato dal cerchio, e la Terra, rappresentata dal quadrato.

Mentre il cerchio rappresenta infatti l'Uno indifferenziato, la dinamicità e la ciclicità del tempo perenne senza inizio né fine, il quadrato rimanda alla sua realizzazione concreta nello spazio e alla stabilizzazione, come fa notare l'esoterista René Guénon che li pone in relazione al corso dell'attuale ciclo cosmico:

«La forma del «Paradiso terrestre», che corrisponde all'inizio di questo ciclo, è circolare, mentre quella della «Gerusalemme celeste», che corrisponde alla sua fine, è quadrata. [...] Si potrebbe dire che è questo cerchio stesso a mutarsi alla fine in un quadrato, poiché le due estremità devono toccarsi, o meglio [...] corrispondersi esattamente.

[...] D'altra parte il mutamento del cerchio in un quadrato equivalente è quanto viene designato come la "quadratura del cerchio"; coloro che dichiarano di quest'ultima che è un problema insolubile, pur se ignorano totalmente il suo significato simbolico, si trovano dunque ad avere di fatto perfettamente ragione, perché tale "quadratura", intesa nel suo vero senso, non potrà essere realizzata che alla fine vera e propria del ciclo.»

(René Guénon, Il Regno della Quantità e i Segni dei Tempi [1945], § 20, Dalla sfera al cubo, trad. it. di Tullio Masera e Pietro Nutrizio, Milano, Adelphi, 1982)

Guénon aggiunge che il quadrato si basa sul numero 4, il più perfetto perché presupposto indispensabile della manifestazione di tutti i numeri e di ogni altra possibilità di sviluppo, come evidenziato dal quaternario comune alle più svariate tradizioni (degli elementi, dei punti cardinali ecc.), oppure dalla tetraktys pitagorica che contiene in sé il denario, cioè il dieci, la totalità. Il 4 in tal caso è rappresentabile anche da una croce che ruotando genera dinamicamente la circonferenza, simbolo del 10, oppure viceversa da un cerchio diviso da una croce in quattro parti, in cui consiste propriamente la «quadratura del cerchio» espressa dalla formula: $10=1+2+3+4.$

Gli stessi significati del cerchio e del quadrato si ritrovano in ambito massonico, simboleggiati dalla sovrapposizione di squadra e compasso, unione degli opposti secondo quanto sostenuto dalla filosofia ermetica: «nella squadra e nel compasso si trova la perfezione del quadrato e del cerchio». Furono inoltre usati in architettura e nelle planimetrie delle città.

Voci correlate

• Nicola Cusano
• Duplicazione del cubo
• Cerchio
• Geometria sacra
• Pietra filosofale
• Quadrato
• Quadratura della parabola
• Squadra e compasso
• Trisezione dell'angolo
• Progetto di legge dell'Indiana sul pi greco

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su quadratura del cerchio

Collegamenti esterni

• (EN) squaring the circle, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• (EN) Eric W. Weisstein, Quadratura del cerchio, su MathWorld, Wolfram Research.
• Far quadrare il cerchio, su cut-the-knot.org.
• La geometria presso gli egizi, su specchiomagico.net. URL consultato il 25 febbraio 2007 (archiviato dall'url originale il 18 marzo 2007).