diff --git "a/CustomView/Advance/Res/\350\247\206\345\233\276\345\235\220\346\240\207\347\263\273.png" "b/CustomView/Advance/Res/\350\247\206\345\233\276\345\235\220\346\240\207\347\263\273.png"
new file mode 100644
index 00000000..aacdd868
Binary files /dev/null and "b/CustomView/Advance/Res/\350\247\206\345\233\276\345\235\220\346\240\207\347\263\273.png" differ
diff --git a/CustomView/Advance/[01]CustomViewProcess.md b/CustomView/Advance/[01]CustomViewProcess.md
index 5166f06f..7f7c72bb 100644
--- a/CustomView/Advance/[01]CustomViewProcess.md
+++ b/CustomView/Advance/[01]CustomViewProcess.md
@@ -178,8 +178,13 @@ onSizeChanged如下：
 
   PS：关于onLayout这个函数在讲解自定义ViewGroup的时候会详细讲解。
 
+<br>
+注意: 这里有一句 view坐标系的相对的. 以前以为所有的坐标点都是基于屏幕左上角 ,其实不然, 而是针对父容器的. 这点真要注意<br>
 
-========
+========   add by Twan
+一张图看懂坐标系:
+
+![](https://github.com/twangithub/AndroidNote/blob/master/CustomView/Advance/Res/%E8%A7%86%E5%9B%BE%E5%9D%90%E6%A0%87%E7%B3%BB.png)
 
 ### 5.绘制内容(onDraw)
 
diff --git a/CustomView/Advance/[09]Matrix_Basic.md b/CustomView/Advance/[09]Matrix_Basic.md
index e60d8bfe..95e41a1b 100644
--- a/CustomView/Advance/[09]Matrix_Basic.md
+++ b/CustomView/Advance/[09]Matrix_Basic.md
@@ -1,3 +1,31 @@
+#### add twan .加上自己的查的资料,便于理解,就是踩坑记录
+> --------------------------------------------------------------------------------
+1.是不是随便两个矩阵都能相乘呢?<br>
+[只有第一个矩阵的列的个数等于第二个矩阵的行的个数，这样的两个矩阵才能相乘。](http://zh.wikihow.com/%E8%AE%A1%E7%AE%97%E7%9F%A9%E9%98%B5%E4%B9%98%E6%B3%95)
+
+2.矩阵是怎么计算结果的呢?<br>
+[结果矩阵第m行与第n列交叉位置的那个值，等于第一个矩阵第m行与第二个矩阵第n列，对应位置的每个值的乘积之和](http://www.ruanyifeng.com/blog/2015/09/matrix-multiplication.html)
+
+3.matrix.preTranslate(8.0f,7.0f);  这是什么意思呢?
+pre是前乘.那么就是M' = M * T
+注意T是什么呢? 在这里T是
+```
+1.0, 0.0, 8.0
+0.0, 1.0, 7.0
+0.0, 0.0, 1.0
+```
+大括号不知道怎么打,能懂就行.刚学的时候误以为是原始矩阵直接乘以
+```
+8.0
+7.0
+1
+```
+须不知大错特错
+
+> --------------------------------------------------------------------------------
+
+
+
 本文内容偏向理论，和 [画布操作](http://www.gcssloop.com/customview/Canvas_Convert/) 有重叠的部分，本文会让你更加深入的了解其中的原理。
 
 本篇的主角Matrix，是一个一直在后台默默工作的劳动模范，虽然我们所有看到View背后都有着Matrix的功劳，但我们却很少见到它，本篇我们就看看它是何方神圣吧。
@@ -71,6 +99,23 @@ Matrix 是一个矩阵，最根本的作用就是坐标转换，下面我们就
 
 ![](http://ww3.sinaimg.cn/large/006tKfTcly1fdz7busaiej3062020mx4.jpg)
 
+-------------------------------------
+请注意这里的:
+```
+X0
+Y0
+1
+```
+实际上完整的写法是这样的:
+```
+0  0  X0
+0  0  Y0
+0  0  1
+```
+
+
+
+-------------------------------------
 >  你可能注意到了，我们坐标多了一个1，这是使用了齐次坐标系的缘故，在数学中我们的点和向量都是这样表示的(x, y)，两者看起来一样，计算机无法区分，为此让计算机也可以区分它们，增加了一个标志位，增加之后看起来是这样: <br/>
 >
 >  (x, y, 1) - 点<br/>
@@ -162,7 +207,7 @@ Matrix 是一个矩阵，最根本的作用就是坐标转换，下面我们就
 
 前乘相当于矩阵的右乘：
 
-![](http://latex.codecogs.com/png.latex?$$ M' =  M \\cdot S $$)
+![](http://latex.codecogs.com/png.latex?$$M'=M\\cdotS$$)
 
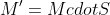
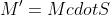
 > 这表示一个矩阵与一个特殊矩阵前乘后构造出结果矩阵。
 
@@ -170,7 +215,7 @@ Matrix 是一个矩阵，最根本的作用就是坐标转换，下面我们就
 
 前乘相当于矩阵的左乘：
 
-![](http://latex.codecogs.com/png.latex?$$ M' =  S \\cdot M $$)
+![](http://latex.codecogs.com/png.latex?$$M'=S\\cdotM$$)
 
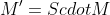
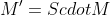
 > 这表示一个矩阵与一个特殊矩阵后乘后构造出结果矩阵。
 
diff --git a/CustomView/Advance/[10]Matrix_Method.md b/CustomView/Advance/[10]Matrix_Method.md
index 6d7b0a0c..d6cb434e 100644
--- a/CustomView/Advance/[10]Matrix_Method.md
+++ b/CustomView/Advance/[10]Matrix_Method.md
@@ -40,15 +40,7 @@ Matrix matrix = new Matrix();
 
 通过这种方式创建出来的并不是一个数值全部为空的矩阵，而是一个单位矩阵,如下:
 
-![](http://latex.codecogs.com/png.latex?$$
-\\left [ 
-\\begin{matrix} 
-1 & 0 & 0 \\\\
-0 & 1 & 0 \\\\
-0 & 0 & 1 
-\\end{1} 
-\\right ]
-$$)
+![](http://latex.codecogs.com/png.latex?$$\\left[\\begin{matrix}1&0&0\\\\0&1&0\\\\0&0&1\\end{1}\\right]$$)
 
 
 #### 有参构造
diff --git a/CustomView/Advance/[11]Matrix_3D_Camera.md b/CustomView/Advance/[11]Matrix_3D_Camera.md
index 0e4c83b6..85f03034 100644
--- a/CustomView/Advance/[11]Matrix_3D_Camera.md
+++ b/CustomView/Advance/[11]Matrix_3D_Camera.md
@@ -319,18 +319,7 @@ public class Rotate3dAnimation extends Animation {
 
 想要解决其实也不难，只要修改两个数值就可以了，这两个数值就是在Matrix中一直被众多开发者忽略的 `MPERSP_0` 和 `MPERSP_1`
 
-![](http://latex.codecogs.com/png.latex?
-$$
-\\left [ 
-\\begin{matrix} 
-MSCALE\\_X & MSKEW\\_X & MTRANS\\_X \\\\
-\\\\
-MSKEW\\_Y & MSCALE\\_Y & MTRANS\\_Y \\\\
-\\\\
-MPERSP\\_0 & MPERSP\\_1 & MPERSP\\_2 
-\\end{1} 
-\\right ] 
-$$)
+![](http://latex.codecogs.com/png.latex?$$\\left[\\begin{matrix}MSCALE\\_X&MSKEW\\_X&MTRANS\\_X\\\\\\\\MSKEW\\_Y&MSCALE\\_Y&MTRANS\\_Y\\\\\\\\MPERSP\\_0&MPERSP\\_1&MPERSP\\_2\\end{1}\\right]$$)
 
 下面是修改后的代码(重点部分都已经标注出来了):