Abstract
We present results from three world-wide campaigns that resulted in the detections of two single-chord and one multi-chord stellar occultations by the plutino object (84922) 2003 VS2. From the single-chord occultations in 2013 and 2014 we obtained accurate astrometric positions for the object, while from the multi-chord occultation on 2014 November 7, we obtained the parameters of the best-fitting ellipse to the limb of the body at the time of occultation. We also obtained short-term photometry data for the body in order to derive its rotational phase during the occultation. The rotational light curve present a peak-to-peak amplitude of 0.141 ± 0.009 mag. This allows us to reconstruct the 3D shape of the body, with principal semi-axes of a = 313.8 ± 7.1 km,  km, and
km, and  km, which is not consistent with a Jacobi triaxial equilibrium figure. The derived spherical volume equivalent diameter of
km, which is not consistent with a Jacobi triaxial equilibrium figure. The derived spherical volume equivalent diameter of  km is about 5% larger than the radiometric diameter of 2003 VS2 derived from Herschel data of 523 ± 35 km, but still compatible with it within error bars. From those results we can also derive the geometric albedo (
km is about 5% larger than the radiometric diameter of 2003 VS2 derived from Herschel data of 523 ± 35 km, but still compatible with it within error bars. From those results we can also derive the geometric albedo ( ) and, under the assumption that the object is a Maclaurin spheroid, the density
) and, under the assumption that the object is a Maclaurin spheroid, the density  for the plutino. The disappearances and reappearances of the star during the occultations do not show any compelling evidence for a global atmosphere considering a pressure upper limit of about 1 microbar for a pure nitrogen atmosphere, nor secondary features (e.g., rings or satellite) around the main body.
for the plutino. The disappearances and reappearances of the star during the occultations do not show any compelling evidence for a global atmosphere considering a pressure upper limit of about 1 microbar for a pure nitrogen atmosphere, nor secondary features (e.g., rings or satellite) around the main body.
Export citation and abstract BibTeX RIS
1. Introduction
Trans-Neptunian objects (TNOs) are bodies that orbit the Sun with an orbital semimajor axis larger than that of Neptune (Jewitt et al. 2008). Due to their large distance to the Sun and low spatial density, those objects do not experience extensive differentiation. Consequently, TNOs are the least evolved bodies in the solar system, at least from the composition point of view. Hence, knowing their physical parameters such as size, shape, albedo, density, presence of atmosphere, rings, and their evolution, yield important information on the nature of material, physical conditions, and history of the primitive solar nebula (Morbidelli et al. 2008), and about the formation and evolution of our solar system (Lykawka & Mukai 2008; Parker 2015; Santos-Sanz et al. 2016). Additionally, the Kuiper belt provides the natural connection with the study of protoplanetary disks observed around other stars (Anglada et al. 2017).
Despite the fact that more than 25 yr have elapsed since this population was discovered (the first TNO discovered was (15760) Albion by Jewitt & Luu (1993), only Pluto and, more recently (in 2019 January 1), the small TNO 2014 MU69 have been visited so far by a spacecraft, the NASA/New Horizons mission (Stern et al. 2019), making them unique bodies in the trans-Neptunian region with a more complete set of information. In summary, our knowledge of basic physical properties of the TNO population is still scarce and fragmentary, mainly due to the faintness and small angular sizes of these bodies as seen from Earth (Stansberry et al. 2008; Lellouch et al. 2013).
In this context, we have been conducting various kinds of Earth-based observations for nearly two decades to gather relevant physical information about TNOs (Lellouch et al. 2002; Ortiz et al. 2002, 2004, 2006, 2007, 2011, 2012, 2015, 2017; Belskaya et al. 2006; Duffard et al. 2008; Assafin et al. 2010, 2012; Thirouin et al. 2010; Sicardy et al. 2011; Braga-Ribas et al. 2013, 2014; Camargo et al. 2014, 2018; Benedetti-Rossi et al. 2016; Bérard et al. 2017; Dias-Oliveira et al. 2017; Leiva et al. 2017). In this framework, we predicted and detected three stellar occultations by the TNO (84922) 2003 VS2—VS2 hereafter—that we monitored through a collaboration with a large panel of amateurs. Among the three events, we obtained two single-chord detections in 2013 December and in 2014 March and one multi-chord detection in 2014 November. The latter observation was made from four well-separated sites, from which valuable physical information is derived, as described in this paper.
The object VS2 was discovered by the Near Earth Asteroid Tracking (NEAT)40 program on 2003 November 14. As a 2:3 resonant object with Neptune, it belongs to the plutino class (MPlanet Center Electronic Circular 2006; Gladman et al. 2008).41 Most of its physical properties were derived from thermal measurements using the space telescopes Herschel and Spitzer (Stansberry et al. 2008; Mommert et al. 2012; Santos-Sanz et al. 2017). Orbital parameters, absolute magnitude, B – R color, rotation period, photometric variation, taxonomy, diameter, and geometric albedo, taken from previously published works, are listed in Table 1.
Table 1. Orbital and Physical Characteristics of the Plutino Object 2003 VS2
| a | q | i | e | Hv* | B – R | P | Δm | Taxon. | D** | pV | APmag |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (au) | (au) | (deg) | (mag) | (mag) | (hr) | (mag) | (km) | (%) | |||
| 39.25 | 36.43 | 14.80 | 0.07 | 4.130 ± 0.070 | 1.52 ± 0.03 | 7.4175285 ± 0.00001 | 0.224 ± 0.013 | BB |

|

|
19.95 |
Note. Orbital parameters: a: semimajor axis in astronomical units; q: perihelion distance in astronomical units; i: orbital inclination in degrees; e: eccentricity—from the JPL Small-Body Database Browser; Hv: average absolute magnitude at the V band obtained from Alvarez-Candal et al. (2016) and private communication; B – R color from Sheppard (2007), Mommert et al. (2012), and references therein; P: preferred rotation period in hours from Santos-Sanz et al. (2017); Δm ![$[{mag}]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn8.gif) : light curve peak-to-valley amplitude from Thirouin (2013); Taxon.: taxonomic color class from Perna et al. (2010), and references therein; D: area-equivalent diameter; pV: geometric albedo at the V band from Mommert et al. (2012) using Herschel and Spitzer data; and APmag: 2003 VS2's average apparent visual magnitude between 2013 and 2014 December from Horizons/JPL (calculated using Hv = 4.2). * Sheppard (2007) and Mommert et al. (2012) obtained a value of Hv = 4.110 ± 0.380; ** Stansberry et al. (2008) obtained a diameter of
: light curve peak-to-valley amplitude from Thirouin (2013); Taxon.: taxonomic color class from Perna et al. (2010), and references therein; D: area-equivalent diameter; pV: geometric albedo at the V band from Mommert et al. (2012) using Herschel and Spitzer data; and APmag: 2003 VS2's average apparent visual magnitude between 2013 and 2014 December from Horizons/JPL (calculated using Hv = 4.2). * Sheppard (2007) and Mommert et al. (2012) obtained a value of Hv = 4.110 ± 0.380; ** Stansberry et al. (2008) obtained a diameter of  km with Spitzer data only.
km with Spitzer data only.
Download table as: ASCIITypeset image
Here we present the results from those three stellar occultations by VS2, with the determination of size and shape of this body based on the multi-chord occultation of 2014 November 7. We also present a rotational light curve for VS2 derived from the 1.5 m telescope located at Sierra Nevada observatory in Granada (Spain), showing an amplitude that is smaller than reported previously in the literature.
We describe in Section 2 the circumstances of observation for the stellar occultations (predictions, updates, and the occultations themselves) and for the photometric runs to obtain the light curve. In Section 3 we describe our data reduction, analysis, and the results obtained from the stellar occultations. We discuss in Section 4 the results concerning the 3D shape of the body as well as other features by combining our occultation and photometric data. Finally, conclusions are presented in Section 5.
2. Observations
Observations performed in this work are separated into three groups: (2.1) observations performed to predict and refine the astrometric positions of the occulted stars and of the object for the occultations; (2.2) observations of the occultations; and (2.3) the observation runs that yielded VS2's rotational light curve.
2.1. Stellar Occultations Predictions and Updates
Stellar occultations require large efforts in order to determine accurate positions of the star and of the object's ephemeris. Despite the fact that the Gaia catalog—on its second data release, GDR2—presents positions and proper motions for stars with unprecedented accuracy (milliarcseconds levels; Gaia Collaboration et al. 2016a, 2016b, 2018; van Leeuwen et al. 2017), the object's ephemeris is usually determined at accuracies of a few hundred milliarcseconds, due to scarce observations. This is larger than the projected sizes of the objects in the sky plane, resulting in misses when attempting stellar occultation observations. Until data from large surveys, such as the Large Synoptic Survey Telescope (LSST),42 become available in a few years from now, regular observations of those small objects will still be needed for most of them in order to improve their orbital parameters. In fact, even with LSST data available, big efforts will still be needed to improve objects' ephemeris, as LSST will mostly cover the southern sky, leaving the objects in the northern hemisphere with big uncertainties. Note also that all those objects have long orbital periods (nearly two centuries for the closest TNOs) and that the time span of the observations are short (less than 20 yr) so the uncertainties in the orbital elements are very sensitive to new observations.
At the time of the three occultations reported here, we did not have the Gaia catalog in our hands so the candidate stars were identified in systematic surveys performed at the 2.2 m telescope of the European Southern Observatory (ESO) at La Silla—IAU code 809, using the Wide Field Imager (WFI). The surveys yielded local astrometric catalogs for 5 Centaurs and 34 TNOs (plus Pluto and its moons) up to 2015, with stars with magnitudes as faint as R mag ∼ 19, see details in Assafin et al. (2010, 2012) and Camargo et al. (2014). All three VS2 occultation candidate stars were then identified in the GDR2 catalog and their R.A., decl., proper motions, and G, B, V, and K magnitudes are presented in Table 2.
Table 2. J2000 Stars Coordinates, Proper Motions, Parallax, and Magnitudes
| Occultation Date | R.A. ICRS | errRA | Decl. ICRS | errDEC | pmRA | pmDEC | Plx | G | B | V | K |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (mas) | (mas) | (mas yr−1) | (mas yr−1) | (mas) | (mag) | (mag) | (mag) | (mag) | |||
| 2013 Dec 12 | 04h36m19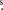 830879 830879 |
0.0502 | +33° 55' 55.45028 | 0.0434 | 0.878 | −0.649 | 0.0733 | 16.0899 | 16.57 | 16.20 | 12.64 |
| 2014 Mar 4 | 04h32m04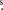 463481 463481 |
0.0548 | +33° 24' 41.95395 | 0.0422 | 2.925 | −3.268 | 0.7682 | 15.9110 | 17.29 | 16.23 | 13.54 |
| 2014 Nov 7 | 04h48m32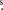 138835 138835 |
0.0406 | +33° 58' 36.40859 | 0.0303 | 7.404 | −8.135 | 1.7609 | 15.1311 | 17.16 | 15.82 | 12.04 |
Note. R.A. and decl. ICRS: barycentric R.A. and decl. (ICRS) propagated to the occultation epoch; errRA and errDEC: standard error of R.A. (multiplied by cosDEC) and decl.; pmRA and pmDEC: proper motion in R.A. (multiplied by cosDEC) and in decl. direction; Plx: absolute stellar parallax; and Gmagnitude. All of the values were obtained from GDR2 (Gaia Collaboration et al. 2016a, 2016b, 2018) and the B, V, and Kmagnitudes were obtained from the NOMAD catalog (Zacharias et al. 2004).
Download table as: ASCIITypeset image
Astrometric updates of the candidate stars (and the TNO when possible) were performed using several telescopes close to the dates of events in Brazil at the Pico dos Dias Observatory—IAU code 874—(Perkin Elmer 1.6 m, Boller & Chivens 0.6 m, and ZEISS 0.6 m), in Spain at the Calar Alto Observatory—IAU code 493—(1.23 m and 2.2 m telescopes), at the Sierra Nevada Observatory—IAU code J86—(1.5 m telescope), and at the Observatorio de La Hitta—IAU code I95—(77 cm telescope), and in France at Pic du Midi—IAU code 586—(T100 cm telescope) so to reduce systematic errors caused by the reference catalogs. Astrometric positions obtained for VS2 with those observations are listed on Table 3. The final positions obtained for the star and the TNO before the occultations provided predictions with uncertainties as large as 50 mas, equivalent to about 1300 km when projected onto Earth's surface.
Table 3. Astrometric Positions for VS2
| Date | R.A. ICRS | Decl. ICRS | Site | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Month | Day | Deg | Min | Sec | Deg | Min | Sec | [IAU Code] |
| 2014 | Feb | 01.868243 | 68 | 03 | 09.4710 | 33 | 36 | 12.4600 | J86 |
| 2014 | Feb | 01.882180 | 68 | 03 | 08.9115 | 33 | 36 | 12.1370 | J86 |
| 2014 | Feb | 01.886832 | 68 | 03 | 08.8125 | 33 | 36 | 11.9780 | J86 |
| 2014 | Feb | 01.891829 | 68 | 03 | 08.5650 | 33 | 36 | 11.8790 | J86 |
| 2014 | Feb | 01.905770 | 68 | 03 | 08.1405 | 33 | 36 | 11.4950 | J86 |
| 2014 | Feb | 03.000210 | 68 | 02 | 31.7055 | 33 | 35 | 44.4050 | J86 |
| 2014 | Feb | 03.004858 | 68 | 02 | 31.5690 | 33 | 35 | 44.2810 | J86 |
| 2014 | Feb | 03.009507 | 68 | 02 | 31.4220 | 33 | 35 | 44.1640 | J86 |
| 2014 | Feb | 03.014154 | 68 | 02 | 31.2825 | 33 | 35 | 44.0510 | J86 |
| 2014 | Feb | 03.018799 | 68 | 20 | 31.0935 | 33 | 35 | 43.9310 | J86 |
| 2014 | Feb | 03.023446 | 68 | 02 | 30.9375 | 33 | 35 | 43.7860 | J86 |
| 2014 | Feb | 03.028092 | 68 | 02 | 30.8565 | 33 | 35 | 43.7010 | J86 |
| 2014 | Feb | 03.032739 | 68 | 02 | 30.6495 | 33 | 35 | 43.5740 | J86 |
| 2014 | Feb | 03.037384 | 68 | 02 | 30.5475 | 33 | 35 | 43.4220 | J86 |
| 2014 | Feb | 03.042029 | 68 | 02 | 30.4290 | 33 | 35 | 43.3400 | J86 |
| 2014 | Feb | 19.920970 | 67 | 58 | 05.7000 | 33 | 29 | 06.1000 | 586 |
| 2014 | Feb | 19.920971 | 67 | 58 | 05.8260 | 33 | 29 | 06.2120 | 586 |
| 2014 | Feb | 19.924510 | 67 | 58 | 05.7000 | 33 | 29 | 06.0000 | 586 |
| 2014 | Feb | 19.924510 | 67 | 58 | 05.7705 | 33 | 29 | 06.1050 | 586 |
| 2014 | Feb | 19.928070 | 67 | 58 | 05.7000 | 33 | 29 | 06.0000 | 586 |
| 2014 | Feb | 19.928074 | 67 | 58 | 05.8995 | 33 | 29 | 06.0400 | 586 |
| 2014 | Feb | 19.931640 | 67 | 58 | 05.7000 | 33 | 29 | 05.8000 | 586 |
| 2014 | Feb | 19.931640 | 67 | 58 | 05.8170 | 33 | 29 | 05.9790 | 586 |
| 2014 | Feb | 19.935207 | 67 | 58 | 05.8155 | 33 | 29 | 05.9290 | 586 |
| 2014 | Feb | 19.935210 | 67 | 58 | 05.7000 | 33 | 29 | 05.8000 | 586 |
| 2014 | Feb | 19.938776 | 67 | 58 | 05.8560 | 33 | 29 | 05.8680 | 586 |
| 2014 | Feb | 19.938780 | 67 | 58 | 05.7000 | 33 | 29 | 05.7000 | 586 |
| 2014 | Feb | 19.942340 | 67 | 58 | 05.7000 | 33 | 29 | 05.7000 | 586 |
| 2014 | Feb | 19.942344 | 67 | 58 | 05.8230 | 33 | 29 | 05.7750 | 586 |
| 2014 | Feb | 19.945910 | 67 | 58 | 05.8500 | 33 | 29 | 05.6000 | 586 |
| 2014 | Feb | 19.945910 | 67 | 58 | 05.8620 | 33 | 29 | 05.7090 | 586 |
| 2014 | Feb | 19.949476 | 67 | 58 | 05.8080 | 33 | 29 | 05.5710 | 586 |
| 2014 | Feb | 19.949480 | 67 | 58 | 05.7000 | 33 | 29 | 05.4000 | 586 |
| 2014 | Feb | 19.953040 | 67 | 58 | 05.8500 | 33 | 29 | 05.4000 | 586 |
| 2014 | Feb | 19.953041 | 67 | 58 | 05.9040 | 33 | 29 | 05.4890 | 586 |
| 2014 | Feb | 19.956608 | 67 | 58 | 05.8545 | 33 | 29 | 05.3620 | 586 |
| 2014 | Feb | 19.956610 | 67 | 58 | 05.7000 | 33 | 29 | 05.2000 | 586 |
| 2014 | Feb | 19.963670 | 67 | 58 | 05.8500 | 33 | 29 | 05.1000 | 586 |
| 2014 | Feb | 19.967230 | 67 | 58 | 05.7000 | 33 | 29 | 05.0000 | 586 |
| 2014 | Feb | 19.970800 | 67 | 58 | 05.7000 | 33 | 29 | 05.1000 | 586 |
| 2014 | Feb | 23.832322 | 67 | 58 | 25.3935 | 33 | 27 | 42.0770 | I95 |
| 2014 | Feb | 23.833071 | 67 | 58 | 24.9570 | 33 | 27 | 41.8390 | I95 |
| 2014 | Feb | 23.835317 | 67 | 58 | 25.4850 | 33 | 27 | 41.7380 | I95 |
| 2014 | Feb | 23.836792 | 67 | 58 | 24.8685 | 33 | 27 | 41.7520 | I95 |
| 2014 | Feb | 23.840530 | 67 | 58 | 25.2300 | 33 | 27 | 41.8910 | I95 |
| 2014 | Feb | 23.841275 | 67 | 58 | 25.2330 | 33 | 27 | 42.0330 | I95 |
| 2014 | Sep | 24.148195 | 72 | 47 | 13.9545 | 33 | 53 | 41.9090 | 493 |
| 2014 | Sep | 24.157750 | 72 | 47 | 13.8450 | 33 | 53 | 42.0140 | 493 |
| 2014 | Sep | 24.167348 | 72 | 47 | 13.6620 | 33 | 53 | 42.1710 | 493 |
| 2014 | Sep | 24.172112 | 72 | 47 | 13.5675 | 33 | 53 | 42.2450 | 493 |
| 2014 | Sep | 24.181729 | 72 | 47 | 13.4475 | 33 | 53 | 42.3420 | 493 |
| 2014 | Sep | 24.186538 | 72 | 47 | 13.3410 | 33 | 53 | 42.4430 | 493 |
| 2014 | Sep | 24.196181 | 72 | 47 | 13.1865 | 33 | 53 | 42.5840 | 493 |
| 2014 | Sep | 24.200971 | 72 | 47 | 13.1190 | 33 | 53 | 42.6250 | 493 |
| 2014 | Sep | 24.205804 | 72 | 47 | 13.0065 | 33 | 53 | 42.7340 | 493 |
| 2014 | Sep | 24.210612 | 72 | 47 | 12.9735 | 33 | 53 | 42.7860 | 493 |
| 2014 | Sep | 24.215402 | 72 | 47 | 12.9045 | 33 | 53 | 42.8490 | 493 |
Note. Positions obtained with the ESO 2p2 telescope—IAU code 809—under mission 090.C-0118(A) are published in Camargo et al. (2014).
Download table as: ASCIITypeset image
2.2. Stellar Occultations
For each of the three stellar occultations, an alert was triggered at several potential sites, resulting in data collected with a large diversity of instruments, see Tables 4–6. All sites used robust clock synchronizations, either by a global positioning system (GPS) or by setting up the clocks using Internet servers—network time Pprotocol (NTP), and acquisition times of each image were inserted on the image header or printed on individual video frames. Using any of those synchronization methods, the times should not present absolute errors larger than 1 ms (Deeths & Brunette 2001). At all sites with favourable weather conditions, data were collected from about 10 minutes prior to the predicted occultation times until about 10 minutes after those times. No filters were used in any of the observations to maximize photon fluxes, and thus signal-to-noise-ratio (S/N).
Table 4. Observation Details of the Single-chord Stellar Occultations
| 2013 Dec 12 | |||||
| Site Name | Longitude (E) | Telescope Aperture | Exposure Time | ||
| (Location) | Latitude (N) | Detector/Instrument | Cycle Time | Observers | Detection |
| [IAU Code] | Altitude (m) | (s) | |||
| Les Makes Observatory | 55° 24' 36 0 0 |
60 cm | 0.75000 | J. Lecacheux | |
| (La Réunion, France) | −21° 11' 58 4 4 |
Raptor Merlin 246 | 0.75031 | A. Peyrot, T.-P. Baum | Positive |
| [181] | 992 | J.-P. Teng | |||
| 2014 Mar 4 | |||||
| Site Name | Longitude (E) | Telescope Aperture | Exposure Time | ||
| (Location) | Latitude (N) | Detector/Instrument | Cycle Time | Observers | Detection |
![$[\mathrm{IAU}\ \mathrm{Code}]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn10.gif)
|
Altitude (m) | (s) | |||
| Wise Observatory | 34° 45' 43 60 60 |
100 cm | 4 | ||
| (Mitzpe Ramon, Israel) | 30° 35' 50 38 38 |
Roper PVCAM | 7 | S. Kaspi | Positive |
| [097] | 884 | PI 1300B/LN | |||
| Wise Observatory | 34° 45' 43 92 92 |
70 cm | 5 | ||
| (Mitzpe Ramon, Israel) | 30° 35' 48 23 23 |
FLI | 6.5 | N. Brosch | Positive |
| [097] | 865 | PL16801 | |||
| West Park Observatory | 358° 23' 31 98 98 |
20 cm | 5.08 | ||
| (Leeds, UK) | 53° 50' 15 42 42 |
WATEC | 5.08 | A. Pratt | Negative |
![$[Z92]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn11.gif)
|
114 | WAT-910HX/RC (x256) | (video) | ||
| Puimichel Observatory | 06° 01' 15 5 5 |
104 cm | 0.25000 | J. Lecacheux | |
| (Puimichel, France) | 43° 58' 48 7 7 |
Raptor Merlin 246 | 0.25031 | S. Moindrot | Negative |
| ⋯ | 724 | ||||
| Weizmann | 34° 48' 45 76 76 |
41 cm | ⋯ | ||
| (Kraar, Israel) | 31° 54' 29 1 1 |
SBIG | ⋯ | I. Manulis | Overcast |
| ⋯ | 107 | ST-8XME CCD | |||
| Sasteria Observatory | 25° 58' 16 37 37 |
25 cm | ⋯ | ||
| (Crete, Greece) | 35° 04' 11 12 12 |
N/A | ⋯ | F. Feys | Overcast |
| ⋯ | 395 | ||||
Note. FLI stands for Finger Lakes instruments, PI for Princeton instruments, PL for pro line, and N/A for not available.
Download table as: ASCIITypeset image
Table 5. Observation Details of the Multi-chord Stellar Occultation on 2014 November 7 with Data Acquisition
| Site Name | Longitude (E) | Telescope Aperture | Exposure Time | ||
|---|---|---|---|---|---|
| (Location) | Latitude (N) | Detector/Instrument | Cycle Time | Observers | Detection |
| (IAU Code) | Altitude (m) | (s) | |||
| Bosque Alegre | 295° 27' 01 5 5 |
154 cm | 5 | C. A. Colazo | |
| (Cordoba, Argentina) | −31° 35' 54 0 0 |
CMOS ZWO ASI120MM | 5.000032 | R. Artola | Positive |
| [821] | 1213.1 | R. Melia | |||
| Rosário | 299° 21' 09 0 0 |
49 cm | 3 | ||
| (Rosário, Argentina) | −32° 58' 16'' | CCD KAF 8300 | 4 | V. Buso | Positive |
| ⋯ | 31.0 | ||||
| Montevideo | 303° 48' 37.1 | 46 cm | 3 | G. Tancredi | |
| (Montevideo, Uruguay) | −34° 45' 20 0 0 |
FLI | 4 | S. Roland | Positive |
| ⋯ | 130.0 | PL9000 | L. Almenares | ||
| A. Ceretta | |||||
| Santa Rosa | 295° 40' 32 5 5 |
20 cm | 25 | ||
| (Santa Rosa, Argentina) | −36° 38' 16 0 0 |
CCD Meade DSI-I | 26 | J. Spagnotto | Positive |
![$[I48]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn12.gif)
|
182.0 | ||||
| ESO—VLT | 289° 35' 49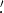 9 9 |
400 cm | 0.00664 | ||
| (Cerro Paranal, Chile) | −24° 37' 31 5 5 |
HAWK-I | 0.00667 | V. D. Ivanov | Negative |
| [309] | 2635.0 | ||||
| ESO - La Silla | 289° 15' 58 5 5 |
355 cm | 0.1 | B. Sicardy | |
| (La Silla, Chile) | −29° 15' 32 3 3 |
NTT/SOFI | 0.10003 | D. Bérard | Negative |
| [809] | 2345.4.0 | ||||
| TRAPPIST-S | 289° 15' 38 2 2 |
60 cm | 3 | C. Opitom | |
| (La Silla, Chile) | −29° 15' 16 6 6 |
TRAPPIST-S | 4.5 | E. Jehin | Negative |
![$[I40]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn13.gif)
|
2317.7 | ||||
| PROMPT | 289° 11' 05 5 5 |
40 cm | 4 | ||
| (Cerro Tololo, Chile) | −30° 09' 56 3 3 |
PROMPT | 6 | J. Pollock | Negative |
| [807] | 2225.0 | ||||
| Las Cumbres* | 289° 11' 42 7 7 |
100 cm | 3/4 | ||
| (Las Cumbres, Chile) | −30° 10' 02 6 6 |
FLI | 5/6 | F. Bianco | Negative |
![$[W85]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn14.gif)
|
2201.7 | MicroLine 4720 | |||
| Dall Kirkham 50 cm | 3 | A. Maury | Negative | ||
| San Pedro de Atacama | 291° 49' 13 2 2 |
Apogee U42 | 4 | ||
| (S. P. de Atacama, Chile) | −22° 57' 12 1 1 |
||||
![$[I16]$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn15.gif)
|
2398.50 | Ash2 Newtonian 40 cm | 15 | N. Morales | Negative |
| SBIG-STL11000 | 17.59 | ||||
| OPD/LNA | 314° 25' 03 0 0 |
Perkin Elmer 160 cm | 2 | G. Benedetti-Rossi | |
| (Itajubá, Brazil) | −22° 32' 04'' | Andor IXON | 2.950 | B. Morgado | Negative |
| [874] | 1864.0 | DU-888E-C00-#BV | A. R. Gomes-Junior | (w/ clouds) | |
Note. FLI stands for Finger Lakes instruments, PI for Princeton instruments, and PL for pro line. * Three 1 m telescopes were used at Las Cumbres (IAU codes W85, W86, and W87). One of them used the Ifilter to minimize the moon contamination while the other two observed in Clear. Exposure time were 3 s for two telescopes (filters I and Clear) and 4 s for the third telescope. Readout time is not constant for this observation, but on average is 2 s. Computers are synchronized via NTP to the site GPS and the start of exposure in the three telescopes had a time shift in order to combine the three data sets and obtain one unique light curve without readout time.
Download table as: ASCIITypeset image
Table 6. Observation Details of the Multi-chord Stellar Occultation on 2014 November 7 with No Data Acquired
| Site Name | Longitude (E) | Telescope Aperture | ||
|---|---|---|---|---|
| (Country) | Latitude (N) | Detector/Instrument | Observers | Situation |
| Altitude (m) | ||||
| Brasília | 312° 07' 04 02 02 |
G11 35 cm | ||
| (Brazil) | −15° 47'' 40 37 37 |
SBIG | P. Cacella | Overcast |
| 1096 | ST8XMEI | |||
| Vitória (UFES) | 319° 41' 33 18 18 |
GSO 35 cm | ||
| (Brazil) | −20° 16' 41 43 43 |
SBIG | M. Malacarne | Overcast |
| 6 | ST8XME | |||
| Oliveira (SONEAR) | 315° 10' 27 88 88 |
45 cm | ||
| (Brazil) | −20° 42 54.27 | FLI | C. Jacques | Overcast |
| 984 | 16803 | |||
| U. Autónoma Tomás Frías | 295° 22' 33 00 00 |
Cassegrain 60 cm | ||
| (Bolivia) | −21° 35' 45 90 90 |
FLI | R. Condori | Overcast |
| 1866 | IMG1001E | |||
| São Carlos (UFSCar) | 312° 06' 50 11 11 |
Meade LX200 30 cm | ||
| (Brazil) | −21° 58' 49 01 01 |
SBIG | G. Rojas | Overcast |
| 847 | ST9 | |||
| Guaratinguetá (UNESP) | 314° 48' 29 50 50 |
Meade LX200 40 cm | ||
| (Brazil) | −22° 48' 10 02 02 |
SBIG | R. Sfair | Overcast |
| 573 | ST-7XME | |||
| Rio de Janeiro (ON) | 316° 46' 32,83'' | Meade LX200 30 cm | F. Braga-Ribas | |
| (Brazil) | −22° 53' 46,85'' | Raptor Merlin 246 | J. I. B. Camargo | Overcast |
| 29 | ||||
| São José dos Campos (INPE) | 314° 08' 16'' | C11 28 cm | ||
| (Brazil) | −23° 12' 33'' | SBIG | A. C. Milone | Overcast |
| 975 | ST-7XE | |||
| Ponta Grossa (UEPG) | 309° 53' 41 39 39 |
Meade RC40 40 cm | ||
| (Brazil) | −25° 05' 40 27 27 |
SBIG | M. Emilio | Overcast |
| 910 | ST-6303E | |||
| Foz do Iguaçu | 305° 24' 22 55 55 |
C11 28 cm | ||
| (Brazil) | −25° 26' 05 45 45 |
SBIG | D. I. Machado | Overcast |
| 185 | ST-7XME | |||
| CASLEO | 290° 41' 15 9 9 |
215 cm | ||
| (Argentina) | −31° 47' 54 7 7 |
PI-2048B | R. Gil-Hutton | Overcast |
| 2552 | ||||
| Montevideo | 303° 48' 37.1 | Meade LX200 30 cm | G. Tancredi | |
| (Uruguay) | −34° 45' 20 0 0 |
Raptor Merlin 246 | S. Roland | Star not detected |
| 130.0 | L. Almenares | |||
| A. Ceretta | ||||
Note. FLI stands for Finger Lakes instruments and PI for Princeton instruments.
Download table as: ASCIITypeset image
Out of 23 stations distributed in nine countries (France, Israel, United Kingdom, Greece, Argentina, Uruguay, Chile, Brazil, and Bolivia), we obtained two single-chord events and one multi-chord occultation, for a total of seven positive detections. Note that the 2014 March occultation was detected by two telescopes at the same site in Israel. As such, they do not provide any constraint on the shape of the object, and we consider it as a single-chord detection. Figures 1–3 show the post-occultation, reconstructed maps for the three events. Note that in those figures we used a radius for VS2 of 564.8 km (determined from the multi-chord occultation), but we do not know the rotational phase for the two single-chord occultations, so the shadow path may be smaller than this value. Details of the data analysis for each occultation are given in Section 3.
Figure 1. Post-occultation map for the 2013 December 12 occultation. North is up and east is right. Blue lines represent the object equivalent diameter from the 2014 November 7 occultation of 564.8 km. Red dots represent the position of the center of the body spaced every 30 s, the bigger dot corresponding to 20:10:44 UTC. The direction of the shadow is shown by the arrow at the right corner. The green dot is the site position with positive detection (see Table 4).
Download figure:
Standard image High-resolution imageFigure 2. Post-occultation map for the 2014 March 4 occultation. North is up and east is right. Blue lines represent the object equivalent diameter from the 2014 November 7 occultation of 564.8 km. Red dots represent the position of the center of the body spaced every 30 s, the bigger dot corresponding to 19:55:54 UTC. The direction of the shadow is shown by the arrow at the right corner. The green dot is the site position with positive detection, while the blue dots are the negative detections and the white dots are the sites with weather overcast (see Table 4).
Download figure:
Standard image High-resolution imageFigure 3. Post-occultation map for the 2014 November 7 occultation. North is up and east is right. Blue lines represent the object equivalent diameter obtained from this occultation, of 564.8 km. Red dots represent the position of the center of the body spaced every 30 s with the bigger one corresponding to 04:22:00 UTC. The direction of the shadow is shown by the arrow at the right corner. The green dots are the site positions with positive detections, while the blue dots are the negative detections and the white dots are the sites with weather overcast (see Tables 5 and 6).
Download figure:
Standard image High-resolution image2.3. Rotational Light Curve
In order to determine the rotational phase of VS2 at the time of the multi-chord occultation, we performed a photometric follow up of the object a few days after the event. We obtained a total of 97 images of VS2 over three nights—2014 November 15, 16, and 17—with the 2k × 2k CCD of the 1.5 m telescope at Sierra Nevada Observatory in Granada (Spain). The image scale of the instrument is 0 232 pixel−1 with a field of view (FOV) of 7
232 pixel−1 with a field of view (FOV) of 7 92 × 7
92 × 7 92. All of the images were acquired without filter and in 2 × 2 binning mode to maximize S/N. The integration time was 300 s throughout the three nights with a Moon illumination of 36% during the first night and 18% during the third night. The average seeing during the three nights was 3
92. All of the images were acquired without filter and in 2 × 2 binning mode to maximize S/N. The integration time was 300 s throughout the three nights with a Moon illumination of 36% during the first night and 18% during the third night. The average seeing during the three nights was 3 3. We pointed the telescope at the same coordinates on the three nights in order to use the same reference stars and thus minimize systematic photometric errors.
3. We pointed the telescope at the same coordinates on the three nights in order to use the same reference stars and thus minimize systematic photometric errors.
Standard bias and flat-field corrections were applied on science images. Specific routines written in interactive data language (IDL) were developed to perform the aperture photometry of all the chosen reference stars and VS2. We tried different apertures for the target, calibration stars, and sky ring annulus in order to maximize the S/N on the object for each night and to minimize the dispersion of the photometry.
The flux of VS2 relative to the comparison stars is finally obtained versus the Julian date, accounting for light travel times. The procedures we used were identical to those detailed in Fernández-Valenzuela et al. (2016, 2017). We folded the final photometric data with the well-known rotational period for VS2 obtained in Santos-Sanz et al. (2017), P = 7.4175285 ± 0.00001 hr. From this rotational light curve, we deduce that VS2 was near one of its absolute brightness maxima at the time of the 2014 November 7 stellar occultation (Figure 4), which implies that the object occulted the star when its apparent surface area was near its maximum. These folded data are also fitted with a second-order Fourier function in order to obtain the peak-to-valley amplitude of the rotational light curve, which turns out to be 0.141 ± 0.009 mag (as listed in Table 10). The decrease in the peak-to-peak amplitude, compared to the value obtained by Thirouin (2013), is probably due to geometric effects (i.e., a change in the aspect angle with respect to the previous amplitude estimations). The epoch for zero phase was chosen to be near the time of occultation (2014 November 7 at 04:00:00 UTC).
Figure 4. Rotational light curve for VS2 obtained on 2014 November 15 (in red), 16 (in blue), and 17 (in green) at Sierra Nevada Observatory (see the text for details) just a few days after the occultation. Light blue dots on the bottom panel show the residuals between the observed points and the fit (blue line). The estimated rotational phase for the 2014 November stellar occultation is near one of the brightness maxima. We used the occultation date as the zero phase date.
Download figure:
Standard image High-resolution image3. Stellar Occultation Data Analysis
Some observations involved in the multi-chord event recorded only the integer part of the second in each image header. It was then necessary to retrieve the fractional part of the second for the mid-exposure time of each image by performing a linear fit to the set, see details in Sicardy et al. (2011) and Dias-Oliveira et al. (2017). From the linear fit we then retrieve the fraction of second for each image with an internal accuracy that depends on the square root of the number of images used, which is less than 0.1 s in practice.
Data obtained in video format from West Park Observatory was converted to flexible image transport system (fits) format using the same procedure as described in Benedetti-Rossi et al. (2016) and Buie & Keller (2016).
The two single-chord events were analyzed to obtain the stellar flux (plus the faint, background contribution due to the occulting body) ratioed to nearby calibration stars using procedures based on the standard Daophot IDL routines (Stetson 1987). The multi-chord occultation was harder to analyze. Since the S/N of the comparison and target stars were too low in all data sets, using the IDL routines the derived chords did not produce satisfactory results, as they presented sizes and positions that did not fit a reasonable and realistic ellipse in the sky plane. We then subjected the data sets to a careful treatment by the new photometry task version of the Program for Reduction of Astronomical Images Automatically (PRAIA; Assafin et al. 2011).
PRAIA uses differential aperture photometry and it differs from the IDL routines in many instances, presenting many useful features for which description is beyond the scope of this work. Among them, the apertures, sky ring sizes, and widths are automatically optimized for better S/N (outside of the event) for each image, following a thorough aperture centering procedure, and the flux is precisely corrected for the variable apertures for all objects on each image. Calibration fluxes are smoothed and the best set of calibration stars is set automatically as a function of the best light curve standard deviation. The flux ratio versus time is further corrected by atmospheric systematic factors (using the observed flux before and after the event) by applying a polynomial fit (we used the third degree in all cases). Finally, the flux ratio is normalized and the resulting normalized light curve stored with many kinds of information (errors, photometry parameters, etc.). Note that the three stars magnitudes are about 16, while it is almost 20 for the TNO. This means that VS2 is not visible in any of the equipment and exposure setup used in the observations and the stars disappear completely during the three occultations, with no residual light from VS2, i.e., we assume that the flux drops to zero in each of these observations. The resulting light curves with positive occultation detections are presented in Figure 5. The light curves flux standard deviation are 21.8% for the 2013 occultation, 12.9% and 6.6% for the two telescopes of 0.7 m and 1 m, respectively, from the 2014 March event, while it is 6.9% for Bosque Alegre, 14.7% for Rosário, 14.5% for Santa Rosa, and 13.1% for Montevideo in the multi-chord occultation.
Figure 5. Normalized light curves of the positive detections of the stellar occultations—see Tables 4 and 5 for site details. Top: single-chord event in 2013 December 12; center: single-chord event in 2014 March 4, showing the detection with the two telescopes at the same site; bottom: multi-chord event on 2014 November. Chords are shifted in flux for better visualization. Vertical lines are the uncertainties in photometry for each point.
Download figure:
Standard image High-resolution imageThe start (star disappearance) and end (star reappearance) times of the occultation are determined by fitting each event by a sharp opaque edge model, after convolution by (i) Fresnel diffraction, (ii) finite CCD bandwidth, (iii) finite stellar diameter, and (iv) finite integration time (see details in Widemann et al. 2009; Braga-Ribas et al. 2013; Ortiz et al. 2017). Note that the Fresnel monochromatic diffraction operates over the Fresnel scale  , where λ is the wavelength of observation and D is the geocentric distance of the object.
, where λ is the wavelength of observation and D is the geocentric distance of the object.
The stellar diameter projected at VS2's distance is estimated using the B, V, and K apparent magnitudes provided by the NOMAD catalog (Zacharias et al. 2004) and the formulae of van Belle (1999)—see Table 2. Using the apparent TNO motion relative to the star, it is possible to express the integration times in actual distances traveled between adjacent data points in the sky plane. Each effect is evaluated in Table 7. We note that our data are dominated by the integration times, and not by Fresnel diffraction or stellar diameter. The occultation timings are then obtained by minimizing a classical χ2 function, using the same procedures as described in Sicardy et al. (2011).
Table 7. Highest Amplitude of Effects to Consider in Order to Determine the Start and End Instants of the Three Stellar Occultations
| Occultation Date | Da | Fresnelb | Star Diameterc | Integration Timed |
|---|---|---|---|---|
| (au) | (km) | (km) | (km) | |
| 2013 Dec 12 | 35.58 | 1.73 | 0.41 | 18.7 |
| 2014 Mar 4 | 36.56 | 1.78 | 0.24 | 36.0 |
| 2014 Nov 7 | 35.72 | 1.74 | 0.56 | 63.5 |
Notes.
aGeocentric distance in astronomical units from Horizons/JPL (https://ssd.jpl.nasa.gov/horizons.cgi) using JPL#30 and DE431. bFresnel diffraction effect ( ); see the text.
cStellar diameter projected at VS2's geocentric distance calculated using (van Belle 1999) and assuming supergiant stars.
dThe finite integration time is given for the smallest exposure time of the positive detections. It is expressed in kilometers after accounting for the velocity of the body projected in the sky plane; see the text.
); see the text.
cStellar diameter projected at VS2's geocentric distance calculated using (van Belle 1999) and assuming supergiant stars.
dThe finite integration time is given for the smallest exposure time of the positive detections. It is expressed in kilometers after accounting for the velocity of the body projected in the sky plane; see the text.
Download table as: ASCIITypeset image
3.1. Single-chord Events
The single-chord occultation of 2013 December 12 was detected from La Réunion Island and had a shadow velocity of 24.91 km s−1, while the 2014 March 4 event had a shadow velocity of 8.99 km s−1 and it was detected by two telescopes at the same site in Israel (see Table 4 for details). The best fits to the ingress and egress profiles are presented in Figure 6. The occultation durations of  s (La Réunion) and 45.75 ± 1.85 s (Israel) then correspond to occultation chords with lengths of
s (La Réunion) and 45.75 ± 1.85 s (Israel) then correspond to occultation chords with lengths of  km and 411.3 ± 16.6 km, respectively, see Table 8.
km and 411.3 ± 16.6 km, respectively, see Table 8.
Figure 6. Best fit for the star disappearance (left) and reappearance (right) instants of the single-chord events—see Table 4 for sites details. Top: 2013 December 12 occultation; center: 2014 March 4 occultation observed with the 0.7 m telescope; bottom: 2014 March 4 occultation observed with the 1 m telescope. Data points are shown in black, the geometric square well models are in blue, the effect of diffraction is shown in green, the effect of finite integration time is added in the orange, and the red lines show all the effects accounted for and then used for comparison with the actual data points.
Download figure:
Standard image High-resolution imageTable 8. Timings of Star Disappearances and Reappearances
| Occultation Eventa | Disappearanceb | Reappearanceb | Chord Size |
|---|---|---|---|
| (s) | (s) | (km) | |
| 2013 Dec 12 |

|

|

|
| 2014 Mar 4 (1 m) | 71865.15 ± 1.55 | 71910.9±0.3 | 411.3 ± 16.6 |
| 2014 Mar 4 (70 cm) | 71861.25 ± 1.15 |

|

|
| 2014 Nov 7 (BA) | 15903.354 ± 0.646 | 15927.400 ± 0.642 | 517.7 ± 27.8 |
| 2014 Nov 7 (RO) | 15883.351 ± 0.887 | 15913.006 ± 0.670 | 638.5 ± 33.5 |
| 2014 Nov 7 (SR) | 15901.0 ± 8.0 | 15928.0 ± 8.0 | 581 ± 345 |
| 2014 Nov 7 (MO) | 15868.286 ± 0.800 | 15890.583 ± 0.800 | 480.1 ± 34.4 |
Notes. BA: Bosque Alegre; RO: Rosário; SR: Santa Rosa; MO: Montevideo.
aSee Tables 4–6 for occultation details. bTimes are given in seconds after 00:00:00.000 UTC of the occultation day.Download table as: ASCIITypeset image
The timings in Table 8 provide the extremities of the corresponding occultation chords projected in the sky plane. More precisely, they give the position (f, g) of the star projected in the sky plane and relative to the center of the object. The quantities f and g are expressed in kilometers, and counted positively toward local celestial east and celestial north, respectively. Note that the calculated position (f, g) depends on both the ephemeris used for the body and the adopted star position, which are both determined to within a finite accuracy. As such, (f, g) must be corrected by an offset that can be determined if several chords are available, thus pinning down the position of the object's center position relative to the star.
This is not possible for a single-chord event. In that case, a circle was adjusted to each chord using the area-equivalent diameter of 564.8 km in order to determine the center of the TNO in the plane of the sky relative to the star at a prescribed time. Two solutions are then equally possible, depending on whether the center of the body went south or north of the star, as seen from Earth. We consider here the average of the two solutions, still resulting in an accurate astrometric positions for VS2 at the time of the two occultations, with uncertainties smaller than 25 mas for the two single-chord occultations. Note that the diameter used here was obtained from the 2014 November 7 occultation, when the object was at one of the maxima in brightness of the light curve, but we do not know the rotational phase for the other two single-chord occultations. This means that probably the shadow path must be smaller than 564.8 km. Anyway, a difference of 50 km in radius will give an uncertainty of less than 1.7 mas in the object position, which is within the error bars. The object positions in R.A. and decl. corrected by the offsets obtained from the occultations are given in Table 9.
Table 9. Astrometric R.A. and Decl., and the Offsets (f, g) for VS2 Derived from the Three Stellar Occultations
| Occultation Date | R.A. ICRS | Decl. ICRS | fa | ga |
|---|---|---|---|---|
| (JPL30 and DE431 + Offset) | (mas) | (mas) | ||
| 2013 Dec 12 20:13:00.000 | 04h36m19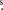 83798 83798 |
+33° 55' 55 2525 2525 |
−15.7 ± 2.4 | −17.5 ± 8.1 |
| 2014 Mar 4 19:55:00.000 | 04h32m04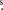 47805 47805 |
+33° 24' 42 0523 0523 |
−12.2 ± 5.4 | −23.7 ± 6.1 |
| 2014 Nov 7 04:22:00.000 | 04h48m32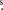 13788 13788 |
+33° 58' 36 1927 1927 |
−60.1 ± 0.3 | −24.5 ± 0.4 |
Note.
aThe offsets depend also on the adopted star positions given on Table 2.Download table as: ASCIITypeset image
3.2. Multi-chord Event
The 2014 November 7 occultation had a typical shadow velocity of 21.53 km s−1 and observers attempted to record the event from 21 different sites. Unfortunately, due to bad weather only eight sites were successful in gathering data, among which four detected the event (see Tables 5 and 6). Despite nondetections, the chords obtained at Cerro Tololo (PROMPT), Las Cumbres, and La Silla (NTT/SOFI; Son of ISAAC Moorwood et al. 1998a, 1998b) provide important constraints on the size of the object, being close to the occultation path.
The resulting light curves with positive detection, shown in Figure 5, provide N = 8 chord extremities, from which we derived the disappearance and reappearance instants of the occultation (see Table 8). The best fits for the ingress and egress times are presented in Figure 7.
Figure 7. Best fit for the star disappearance (left) and reappearance (right) instants of the multi-chord event of 2014 November 7—see Table 5 for sites details. From top to bottom: Bosque Alegre, Rosario, Santa Rosa, and Montevideo. Line colors are the same as in Figure 6.
Download figure:
Standard image High-resolution imageThe shape of the body's limb is assumed to be an ellipse, as adopted in previous works, see Braga-Ribas et al. (2013, 2014), Benedetti-Rossi et al. (2016), Dias-Oliveira et al. (2017), and Ortiz et al. (2017). The ellipse is defined by M = 5 adjustable parameters: the position of the ellipse center, (fc, gc); the apparent semimajor axis, a'; the apparent oblateness,  ' = (a' − b')/a' (where b' is the apparent semiminor axis); and the position angle of the pole P' of b', which is the apparent position angle of the pole measured eastward from celestial north. Note that the center
' = (a' − b')/a' (where b' is the apparent semiminor axis); and the position angle of the pole P' of b', which is the apparent position angle of the pole measured eastward from celestial north. Note that the center  actually measures the offsets in R.A. and decl. to be applied to the adopted ephemeris, assuming that the star position is correct. Note also that the quantities a', b', fc, and gc are all expressed in kilometers.
actually measures the offsets in R.A. and decl. to be applied to the adopted ephemeris, assuming that the star position is correct. Note also that the quantities a', b', fc, and gc are all expressed in kilometers.
The statistical significance of the fit is evaluated from the χ2 per degree of freedom (pdf) defined as  , which should be close to unity for a correct fit. The individual 1σ error bar of each parameter is obtained by varying that parameter from its nominal solution value (keeping the other parameters free), so that χ2 varies from its minimum value
, which should be close to unity for a correct fit. The individual 1σ error bar of each parameter is obtained by varying that parameter from its nominal solution value (keeping the other parameters free), so that χ2 varies from its minimum value  to
to  .
.
Using the timings for the star disappearance and reappearance obtained from the four positive detections (Table 8), we obtain a best-fitting ellipse with  and its parameters a' = 313.8 ± 7.1 km,
and its parameters a' = 313.8 ± 7.1 km,  (
( ), (f, g) = (1558.1 ± 8.1, 634.6 ± 11.0) km, and P' = 5° ± 7° with an equivalent radius of
), (f, g) = (1558.1 ± 8.1, 634.6 ± 11.0) km, and P' = 5° ± 7° with an equivalent radius of  km, as shown in Figure 8.
km, as shown in Figure 8.
Figure 8. Occultation chords (blue) and their uncertainties (red) from the multi-chord event of 2014 November with the best elliptical fit (black). The offsets in both axis are with respect to ephemeride positions obtained using JPL#30 and DE431. The arrow shows the direction of the shadow motion and the green lines represent the two closest sites from where there were no detection of the occultation (see Table 5). The equivalent circle (that has the same area as the ellipse) is shown in orange with a diameter of 564.8 km.
Download figure:
Standard image High-resolution image4. Results
4.1. Size and Shape
Homogeneous rocky objects with diameters on the order of 1000 km or more are expected to have reached the hydrostatic equilibrium, assuming Maclaurin spheroidal or Jacobi ellipsoidal shapes (Chandrasekhar 1987). The critical diameter allowing to reach this equilibrium is discussed by Tancredi & Favre (2008). In particular, hydrostatic equilibrium could be reached for smaller objects, if made of ices or of a combination of ices and rocks. Nevertheless, the formation scenario and collisional history of individual objects are not known, allowing objects with complex internal structures (i.e., differentiated density layers, granular for a peeble accretion scenario, etc.). Thus, we cannot discard solutions that diverge somewhat from the expected equilibrium figure given by Chandrasekhar (1987). The case of the dwarf planet Haumea (Ortiz et al. 2017) is a good example of a body with sizes that does not match a hydrostatic equilibrium figure for a geologically homogeneous fluid body.
Figure 9. Light curve from the single-chord stellar occultation of 2014 March 4 obtained at the Wise Observatory (black) and the two models for the isothermic pure nitrogen (red) and Pluto-like (blue) atmospheres within a 3σ limit.
Download figure:
Standard image High-resolution imageThe rotational light curve of Figure 4 shows that VS2 is consistent with an object having a triaxial ellipsoidal shape. The short-term photometry of the body presented in Section 2.3 showed that the multi-chord occultation took place near one of the absolute brightness maxima of the rotational light curve, meaning that VS2 occulted the star when its apparent surface area was near its maximum. Assuming a triaxial shape, this occurs when its longest axis a was perpendicular to the line of sight, so that the semimajor axis of the projected ellipse a' is equal to the real 3D axes. With the known rotation period and phase, we verified if it was possible to use one or the two single-chord occultation results to improve the accuracy on the determination of size and shape for the TNO. The problem is that even if the rotational phase and period are well determined, the ephemeris for the object is not well constrained, with uncertainties of about 50 mas, in a way that the chord from the two occultations can fit anywhere in the multi-chord apparent ellipse. With this uncertainty we could not use any of the other chords to obtain further constraints on VS2's shape using the same method that Dias-Oliveira et al. (2017) did for the TNO 2003 AZ84.
Considering the limb fit to the apparent ellipse obtained from the multi-chord occultation and the light curve amplitude, we can use the same procedure as in Sicardy et al. (2011; also used in Braga-Ribas et al. 2013 and Ortiz et al. 2017) to derive the three axes of the body. Our best solution for a triaxial shape has semi-axis values of a = 313.8 ± 7.1 km,  km (
km ( ), and
), and  km (
km ( ), with the c-axis inclined
), with the c-axis inclined  with respect to the observer, which is not consistent with the Jacobi equilibrium figure—see the Appendix for details. This solution gives a spherical volume equivalent diameter of
with respect to the observer, which is not consistent with the Jacobi equilibrium figure—see the Appendix for details. This solution gives a spherical volume equivalent diameter of  , from which we can derive (using Hv = 4.130 ± 0.070 mag) the geometric albedo
, from which we can derive (using Hv = 4.130 ± 0.070 mag) the geometric albedo  .
.
Since we cannot make any constraint about VS2's density using the triaxial approach without making any other assumption of its mass, we can make an assumption that VS2 has an oblate shape, as a Maclaurin equilibrium figure with a semi-axis of a = 313.8 km and 254.8 ≤ c ≤ 313.8 km. Note that with this assumption, we are also assuming that the light curve amplitude variation is due to albedo features. Making this assumption and combining with the rotation period (given in Table 1), we can derive its density of  kg m−3. All those values are summarized in Table 10.
kg m−3. All those values are summarized in Table 10.
Table 10. Solution for 2003 VS2 Derived from the Multi-chord Stellar Occultation and the Rotational Light Curve
| Parameter | Value |
|---|---|
| a' × b' (km) |

|
| (f, g) (km) 1 | (−1558.1 ± 8.1; −634.6 ± 11.0) |
| Position angle of projected ellipse (deg) | 5 ± 7 |
| Light curve amplitude 2—Δm—(mag) | 0.141 ± 0.009 |
| Geometric albedo—pV |
 . . |
| a × b × c (km) |

|
| Aspect angle (deg) |

|
| Equivalent diameter (km) |

|
| Density—Maclaurin (kg m−3) |

|
Note.1 Offsets obtained with respect to JPL30 + DE431. It also depends on the star position given in Table 2. 2 Period used to fit was 7.4175285 ± 0.00001 hr from Santos-Sanz et al. (2017).
Download table as: ASCIITypeset image
4.2. Atmosphere and Secondary Detections
On the largest TNOs the most common volatiles found through spectroscopic studies are water ice (H2O), methane (CH4), ammonia (NH3), molecular nitrogen (N2), and even methanol (CH3OH) and ethane (C2H6) for a few objects (Guilbert et al. 2009; Barucci et al. 2011). In the case of VS2, near-infrared spectra of this body shows the presence of exposed water ice (Barkume et al. 2008), but no other volatile is reported to be detected. Data from the three stellar occultations showed no compelling evidence for a global atmosphere.
Using the same method for Quaoar (Braga-Ribas et al. 2013), we have modeled synthetic occultation light curves using a ray tracing code as described in Sicardy et al. (2011) and Widemann et al. (2009). Several synthetic light curves are then compared to our best light curve obtained at the Wise Observatory on the single-chord occultation on 2014 March 4 providing a range of χ2 with the detection threshold. We test two possible atmospheric models: one with an isothermal N2 atmosphere, as this gas is the most volatile one among those listed above. We consider a typical temperature of 40 K for this model, but the result is weakly dependent on this particular value. The other model is a N2 atmosphere with CH4 as a minor species, starting near 40 K at the surface and ramping up to 100 K near 25 km altitude due to methane infrared absorption, as is observed in Pluto's atmosphere (Hinson et al. 2017).
Our χ2-tests show that for both models, the Wise data are consistent with no atmosphere, with upper limits of 0.2 microbar and 1 microbar at the 1σ and 3σ levels, respectively (see Figure 9).
We also searched for secondary events that may be related to a satellite, ring, or some material orbiting VS2. Using our highest time-resolution light curve—obtained with the 3.5 m European Southern Observatory (ESO) New Technology Telescope (NTT) telescope with 0.1 s of cycle time and roughly positioned 400 km from VS2's center—we can estimate an upper limit of 0.2 km for an opaque object (or 18.5 km for any material with optical depth of 0.1). Considering the best chord with positive detection—from Bosque Alegre with 5 s cycle time—those limits are 107.7 km for opaque and 732 km for material with optical depth of 0.1.
One secondary feature was also detected in the NTT light curve, as shown in Figure 10. The drop has a relative depth of less than 10% (compared to the light curve standard deviation of 8.6%) and a duration of about 29 s, corresponding to a chord length of 625 km. However, this drop remains marginally significant and cannot be confirmed or rejected using the nearby chords from Cerro Tololo (insufficient S/N) and Pico dos Dias (overcast). This drop could be due to an occultation of a companion star by the object, causing a secondary occultation as happened during a stellar occultation by the Centaur object Chariklo in 2014—see Leiva et al. (2017) and Bérard et al. (2017). Note that with the size of VS2 and the geometry of the occultation, the Bosque Alegre positive light curve (data set with the best S/N) should not present any sign of this possible secondary occultation. Also, considering the main star magnitude (V = 15.82) and the drop of 10%, the companion would have a magnitude of V = 18.21. If this star is closer than 0 8 it is likely not to be present in the GDR2 catalog (Brandeker & Cataldi 2019). We estimate that the companion star should be closer than 0
8 it is likely not to be present in the GDR2 catalog (Brandeker & Cataldi 2019). We estimate that the companion star should be closer than 0 5, so the existence of a stellar companion remains consistent with its absence in the GDR2.
5, so the existence of a stellar companion remains consistent with its absence in the GDR2.
Figure 10. Light curve from the multi-chord stellar occultation of 2014 November 7 obtained at La Silla/NTT. All the flux drops in the curve are due to the star being too close to the edge of the CCD or being influenced by the bad row of pixels in the center of the CCD. Note the relative flux drop of 0.09 that happens between instants 15885 and 15915 s, fitted using a square well model, represented by the red line.
Download figure:
Standard image High-resolution imageAnother possibility is that this drop is due to some diffuse material around VS2, but since none of the other light curves show such a secondary event to within the 5σ level, this hypothesis is less likely. Also, a careful look on the NTT images presents some issues. The images have 320 versus 32 pixels with a dead row in the middle of the CCD (row 69). There was only one reference star in the field for photometric calibration, which is fainter than the occulted star, and the telescope tracking was not perfect, in a way that sometimes one or both stars were close to the edge of the CCD. So we cannot completely discard instrumental effects or reduction artifacts on this data set. In conclusion, more occultations are needed in order to confirm or discard the presence of any secondary feature.
5. Conclusions
We observed two single-chord and one multi-chord stellar occultations by the plutino (84922) 2003 VS2. Observations were performed on 2013 December 12 in La Réunion, on 2014 March 4 in Israel, and from 11 sites in South America on 2014 November 7, with four positive detections. The two single-chord events are consistent with the multi-chord solutions but do not bring further constraints to the object shape. However, they provide good astrometric constraints, thus improving the ephemeris of the body.
Using the timings of the 2014 November 7 event, we find the apparent ellipse with area-equivalent diameter of  km. Assuming that VS2 has a triaxial shape and combining the occultation data with the light curve amplitude (Δm = 0.141 ± 0.009) obtained from photometric observations of the TNO, we derive the object 3D shape, with semi-axes of a = 313.8 ± 7.1 km,
km. Assuming that VS2 has a triaxial shape and combining the occultation data with the light curve amplitude (Δm = 0.141 ± 0.009) obtained from photometric observations of the TNO, we derive the object 3D shape, with semi-axes of a = 313.8 ± 7.1 km,  km, and
km, and  km, with the c-axis inclined
km, with the c-axis inclined  with respect to the observer. Those values are not consistent with a Jacobi equilibrium figure, but are in accordance, at the 1σ level, with previous values published by Mommert et al. (2012), Stansberry et al. (2008), and Lellouch et al. (2013) (area-equivalent diameter of
with respect to the observer. Those values are not consistent with a Jacobi equilibrium figure, but are in accordance, at the 1σ level, with previous values published by Mommert et al. (2012), Stansberry et al. (2008), and Lellouch et al. (2013) (area-equivalent diameter of  km).
km).
We also considered the possibility that VS2 is an oblate Maclaurin equilibrium figure (with a = b > c). With this assumption, the light curve amplitude variation is due to albedo features and VS2 would have a density of  kg m−3. The light curve amplitude can be explained in the extreme cases to be due only to the shape (with the triaxial shape model) or to a darker or brighter spot on the surface of about 100 km—16% of object diameter—if VS2 is a Maclaurin.
kg m−3. The light curve amplitude can be explained in the extreme cases to be due only to the shape (with the triaxial shape model) or to a darker or brighter spot on the surface of about 100 km—16% of object diameter—if VS2 is a Maclaurin.
A possible secondary event was detected in the NTT data, that may be caused by the presence of some feature in VS2's surroundings or due to a secondary occultation occurred by the presence of a companion star, but the data are insufficient to make any deep conclusions. We also derived an upper limit for a global atmosphere (either isothermic pure nitrogen or Pluto-like) of 1 microbar (3σ).
Although the rotation period is well defined, and values for the geometric albedo and size of VS2 are well determined with the occultations, its 3D shape (and as a consequence, its density) still need more observations in order to constrain the values obtained in this work.
G.B.-R. is thankful for the support of the CAPES and FAPERJ/PAPDRJ (E26/203.173/2016) grant. Part of the research leading to these results has received funding from the European Research Council under the European Community's H2020 (2014-2020/ERC grant agreement No. 669416 "LUCKY STAR"). The research leading to these results has received funding from the European Union's Horizon 2020 Research and Innovation Programme, under grant agreement No. 687378 (SBNAF). P.S.-S. and J.L.O. acknowledge the financial support by the Spanish grant AYA-2017-84637-R and the Proyecto de Excelencia de la Junta de Andalucía J.A. 2012-FQM1776. P.S.-S., J.L.O., and R.D. acknowledge financial support from the State Agency for Research of the Spanish MCIU through the "Center of Excellence Severo Ochoa" award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709). Based on observations made with ESO Telescopes at the La Silla Paranal Observatory under program ID 094.C-0352. M.A. thanks CNPq (grants 427700/2018-3, 310683/2017-3, and 473002/2013-2) and FAPERJ (grant E-26/111.488/2013). J.I.B.C. acknowledges CNPq grant 308150/2016-3. R.V.-M. thanks grants: CNPq-304544/2017-5, 401903/2016-8, Faperj: PAPDRJ-45/2013, and E-26/203.026/2015. F.B.-R. acknowledges CNPq grant 309578/2017-5. E.F.-V. acknowledges UFC 2017 Preeminent Postdoctoral Program (P3). TRAPPIST-South is a project funded by the Belgian Fonds (National) de la Recherche Scientifique (F.R.S.-FNRS) under grant FRFC 2.5.594.09. F. E.J. is a FNRS Senior Research Associate. A.A.C. acknowledges support from FAPERJ (grant E-26/203.186/2016) and CNPq grants (304971/2016-2 and 401669/2016-5). B.M. thanks the CAPES/Cofecub-394/2016-05 grant. A.R.G.J. and R.S. thank the financial support of FAPESP (proc. 2018/11239-8, proc. 2011/08171-3, proc. 2016/ 24561-0). A.M. thanks Caisey Harlingten for the use of his 50 cm telescope. We thank V. Buso and R. Condori for the observation efforts.
Appendix: Deriving VS2's Shape and Density
We describe here the procedure used to determine the values of the semi-axis of a triaxial ellipsoid ( ) and the angle between the c-axis and the observer (θ).
) and the angle between the c-axis and the observer (θ).
First we have the relations from Sicardy et al. (2011; also used in Braga-Ribas et al. 2013 and Ortiz et al. 2017) between the real c and b semiminor axis and the observed b':

where in our case we have  km as the semiminor axis of the ellipse observed in occultation. Multiplying both sides by 1/a and replacing b/a by β and c/a by γ, we can rewrite Equation (1) and rearrange the terms to have a direct relation of γ as a function of β:
km as the semiminor axis of the ellipse observed in occultation. Multiplying both sides by 1/a and replacing b/a by β and c/a by γ, we can rewrite Equation (1) and rearrange the terms to have a direct relation of γ as a function of β:

Note that since the multi-chord occultation took place near the maximum brightness, we have a'= a, and so β'= b'/a. Second, using Equation (8) from Sicardy et al. (2011; SI) we have

where Δm is the amplitude of the rotational light curve (0.141 ± 0.009 mag; see Table 1). We can rearrange the terms in the equation and obtain another relation of γ as function of β:

where ξ = 10−Δm/1.25. Those two equations combined (Equations (2) and (4)) give us constraints on the values of β for every θ, but without any further assumptions, γ can assume any value from zero (or more specifically, undefined) to β and θ can have values from 0° to 90°.
Now, assuming that VS2 is large enough to achieve hydrostatic equilibrium, we have the limits for β and γ as a Jabobi-shape object. Tancredi & Favre (2008) present the relations Γ—associated with the angular momentum L—and Ω—associated with the angular velocity ω—given respectively by:

and

where G is the gravitational constant, M, R, and ρ are the mass, equivalent radius, and density of the body, respectively. For a Jacobi object, there is a lower and an upper limit for the two quantities: 0.303 ≤ Γ ≤ 0.390, and 0.284 ≤ Ω ≤ 0.374; which also limit the values of β between 0.432 and 1, and γ between 0.345 and 0.583. The shapes of Jacobi ellipsoids in terms of the semi-axes (a, b, and c) can only be obtained by solving Chandrasekhar (1969)—also in Lacerda & Jewitt (2007) and Sicardy et al. (2011) supplementary information—integrals:

and

where ![${\rm{\Delta }}(\beta ,\gamma ,u)={[(1+u)({\beta }^{2}+u)({\gamma }^{2}+u)]}^{1/2}$](https://content.cld.iop.org/journals/1538-3881/158/4/159/revision1/ajab3b05ieqn55.gif) . Once β = b/a is given, Equation (7) yields γ, which in turn allows for the calculation of ω (or ρ), using Equation (8).
. Once β = b/a is given, Equation (7) yields γ, which in turn allows for the calculation of ω (or ρ), using Equation (8).
We can plot the two relations between γ and β for a triaxial body (Equation (2) is represented in Figure 11 and Equation (4) in Figure 12) and verify if there exists a set of possible common solutions for every value of θ. Each of the intersections between the two curves for a same θ are presented as gray lines in Figure 13. If we also plot the Jacobi relation between γ and β (blue line in Figure 13) we should see a solution that intersects the three curves, which is not the case for VS2. This means that there is a solution for a triaxial shape but this solution is not a Jacobi shape.
Figure 11. Relation between β = b/a and γ = c/a obtained using Equation (2). Black lines correspond to a value of θ between 5° and 90° (from left to right), every 5°. The orange line is the value for β = γ. The red dotted vertical line is the value of β' = 0.811, observed in occultation.
Download figure:
Standard image High-resolution imageFigure 12. Relation between β = b/a and γ = c/a obtained using Equation (4). Black lines correspond to a value of θ between 0° and 90° (from left to right), every 5°. The orange line is the value for β = γ. The red dotted vertical line is the value of β' = 0.811, observed in occultation.
Download figure:
Standard image High-resolution imageFigure 13. Relation between β = b/a and γ = c/a combining Equation (2) (black dotted lines—as in Figure 11) and Equation (4) (red dotted lines—as in Figure 12). The blue curve is the intersection between the black and red lines for each value of θ and the uncertainties (dotted blue lines—which depend on the determination of β' and Δm). The orange line is the value for β = γ while the gray line represents the relation for β and γ for the Jacobi shape. For θ between 55° and 80°, defined by the black and red full lines, there is no intersection between the blue and gray lines, meaning that there is no Jacobi solution for VS2.
Download figure:
Standard image High-resolution imageIn the case of VS2 the best solution for a triaxial shape have values for  degrees, with
degrees, with  (
( km),
km),  (
( km). Those values are also given on Table 10.
km). Those values are also given on Table 10.
In order to have a Jacobi solution, we can explore different values for Δm, from zero to the nominal value of 0.141 mag. In fact we are assuming that some of the light curve contribution is due to VS2's shape and some due to albedo variation in the surface. When we try values for Δm smaller than 0.141 the lines in Figure 12 will move to the right and so more intersections with the lines from Figure 11 will be available, i.e., there will be an intersection between the gray and the blue lines in Figure 13. For Δm = 0.015 mag we find a Jacobi solution with β = 0.908 (b = 284.9 km), γ = 0.553 (c = 173.5 km), and θ = 75°.
We can also explore the other extreme and assume that VS2 has an oblate Maclaurin shape (with semi-axis a = b = 313.8 ± 7.1 km and 254.8 ≤ c ≤ 313.8 km). This assumption automatically imposes that the light curve amplitude variation is only due to albedo features on VS2's surface. Considering the light curve amplitude of 0.141 ± 0.009 mag—see Table 1—the presence of surface irregularities (lumps) and some albedo variegation (spots) on the object with a size approximately of 100 km (∼16% of the object equivalent area) is needed. Note that the Sputnik Planitia in Pluto is nearly 1000 × 800 km across (∼15% of its equivalent area; Hamilton et al. 2016). Considering the Maclaurin shape and using the rotational period (P = 7.4175285 ± 0.00001 hr; see Table 1), we can derive VS2's density of  g cm−3, as show in Figure 14.
g cm−3, as show in Figure 14.
Figure 14. Relation between  and density for a Maclaurin object with rotation period of 7.4175285 hr (black line). The oblateness obtained for VS2 (blue horizontal full and dotted lines) gives limits for the minimum value of the density of 1.4 g cm−3. Blue dotted lines represent the values considering the uncertainties in a and b. The red line is the interval between the limits.
and density for a Maclaurin object with rotation period of 7.4175285 hr (black line). The oblateness obtained for VS2 (blue horizontal full and dotted lines) gives limits for the minimum value of the density of 1.4 g cm−3. Blue dotted lines represent the values considering the uncertainties in a and b. The red line is the interval between the limits.
Download figure:
Standard image High-resolution imageFootnotes
- 40
- 41
Another classification is given by M. Brown in http://web.gps.caltech.edu/~mbrown/dps.html.
- 42


 t 17, B-4000 Liège, Belgium
t 17, B-4000 Liège, Belgium













