Paper:
Stability Analysis of Drilling Inclination System with Time-Varying Delay via Free-Matrix-Based Lyapunov–Krasovskii Functional
Zhen Cai*,**,† and Guozhen Hu**
*Wuhan City Polytechnic University
No.127 Nanli Road, Hongshan District, Wuhan 430064, China
**Hubei Polytechnic University
No.16 Guilin North Road, Xialu District, Huangshi 435003, China
†Corresponding author
This study provides an insight into the asymptotic stability of a drilling inclination system with a time-varying delay. An appropriate Lyapunov–Krasovskii functional (LKF) is essential for the stability analysis of the abovementioned system. In general, an LKF is constructed with each coefficient matrix being positive definite, which results in considerable conservatism. Herein, to relax the conditions of the derived criteria, a novel LKF is proposed by avoiding the positive-definite restriction of some coefficient matrices and introducing additional free matrices simultaneously. Subsequently, this relaxed LKF is applied to derive a less conservative stability criterion for the abovementioned system. Finally, the effect of reducing the conservatism of the proposed LKF is verified based on two examples.
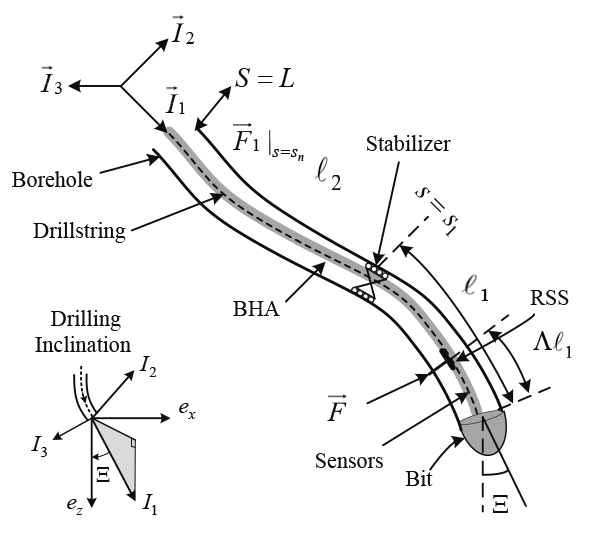
Drilling inclination
- [1] Z. Cai, X. Lai, M. Wu, L. Chen, and C. Lu, “Observer-based trajectory control for directional drilling process,” Asian J. Control, doi: 10.1002/asjc.2456, 2021.
- [2] E. Fridman, “Introduction to Time-Delay Systems: Analysis and Control,” Birkhäuser, 2014.
- [3] M. F. Shakib, E. Detournay, and N. V. D. Wouw, “Nonlinear dynamic modeling and analysis of borehole propagation for directional drilling,” Int. J. Nonlin. Mech., Vol.113, pp. 178-201, 2019.
- [4] É. Gyurkovics, and T. Takács, “Comparison of some bounding inequalities applied in stability analysis of time-delay systems,” Syst. Control Lett., Vol.123, pp. 40-46, 2019.
- [5] H.-B. Zeng, Y. He, M. Wu, and J. H. She, “Free-matrix-based integral inequality for stability analysis of systems with time-varying delay,” IEEE Trans. Automat. Control, Vol.60, No.10, pp. 2768-2772, 2015.
- [6] X. Liu and D. Zhao, “New stability criterion for time-delay systems via an augmented Lyapunov–Krasovskii functional,” Appl. Math. Lett., Vol.116, Artcle No. 107071, 2021.
- [7] Y. He, Q. G. Wang, C. Lin, and M. Wu, “Augmented Lyapunov functional and delay-dependent stability criteria for neutral systems,” Int. J. Robust Nonlin. Control, Vol.15, pp. 923-933, 2005.
- [8] X.-M. Zhang, Q.-L. Han, A. Seuret, and F. Gouaisbaut, “An improved reciprocally convex inequality and an augmented Lyapunov–Krasovskii functional for stability of linear systems with time-varying delay,” Automatica, Vol.84, pp. 221-226, 2017.
- [9] T. H. Lee and J. H. Park, “A novel Lyapunov functional for stability of time-varying delay systems via matrix-refined-function,” Automatica, Vol.80, pp. 239-242, 2017.
- [10] C. K. Zhang, Y. He, L. Jiang, and M. Wu, “Notes on stability of time-delay systems: bounding inequalities and augmented Lyapunov-Krasovskii functionals,” IEEE Trans. Automat. Control, Vol.60, No.10, pp. 5331-5336, 2017.
- [11] L. Ding, Y. He, M. Wu, and Z. Zhang, “A novel delay partitioning method for stability analysis of interval time-varying delay systems,” J. Franklin Inst., Vol.354, pp. 1209-1219, 2017.
- [12] A. Seuret and F. Gouaisbaut, “Wirtinger-based integral inequality: Application to time-delay systems,” Automatica, Vol.49, No.9, pp. 2860-2866, 2013.
- [13] P. Park, W. I. Lee, and S. Y. Lee, “Auxiliary function-based integral inequalities for quadratic functions and their applications to time-delay systems,” J. Franklin Inst., Vol.352, No.4, pp. 1378-1396, 2015.
- [14] J. Chen, S. Xu, and B. Zhang, “Single/Multiple Integral inequalities with applications to stability analysis of time-delay systems,” IEEE Trans. Automat. Control, Vol.62, No.7, pp. 3488-3493, 2017.
- [15] W. I. Lee, S. Y. Lee, and P. G. Park, “Affine Bessel-Legendre inequality: Application to stability analysis for systems with time-varying delays,” Automatica, Vol.93, pp. 535-539, 2018.
- [16] A. Seuret and F. Gouaisbaut, “Stability of linear systems with time-varying delays using Bessel-Legendre inequalities,” IEEE Trans. Automat. Control, Vol.63, No.1, pp. 225-232, 2018.
- [17] Y. He, M. Wu, J.-H. She, and G.-P. Liu, “Delay-dependent robust stability criteria for uncertain neutral systems with mixed delays,” Syst. Control Lett., Vol.51, pp. 57-65, 2004.
- [18] C. K. Zhang, Y. He, L. Jiang, W. J. Lin, and M. Wu, “Delay-dependent stability analysis of neural networks with time-varying delay: A generalized free-weighting-matrix approach,” Appl. Math. Comput., Vol.294, pp. 102-120, 2017.
- [19] C.-K. Zhang, Y. He, L. Jiang, M. Wu, and H.-B. Zeng, “Stability analysis of systems with time-varying delay via relaxed integral inequalities,” Syst. Control Lett., Vol.92, pp. 52-61, 2016.
- [20] C.-K. Zhang, Y. He, L. Jiang, M. Wu, and Q.-G. Wang, “An extended reciprocally convex matrix inequality for stability analysis of systems with time-varying delay,” Automatica, Vol.85, pp. 481-485, 2017.
- [21] A. Seuret, K. Liu, and F. Gouaisbaut, “Generalized reciprocally convex combination lemmas and its application to time-delay systems,” Automatica, Vol.95, pp. 488-493, 2018.
- [22] T. H. Lee, J. H. Park, and S. Xu, “Relaxed conditions for stability of time-varying delay systems,” Automatica, Vol.75, pp. 11-15, 2017.
- [23] Z. Cai, X. Lai, M. Wu, C. Lu, and L. Chen, “Equivalent-input-disturbance-based robust control of drilling trajectory with weight-on-bit uncertainty in directional drilling,” ISA Trans., doi: 10.1016/j.isatra.2021.08.032, 2021.
- [24] Z. Cai, X. Lai, M. Wu, C. Lu, and L. Chen, “Trajectory Azimuth Control Based on Equivalent Input Disturbance Approach for Directional Drilling Process,” J. Adv. Comput. Intell. Intell. Informa., Vol.25, No.1, pp. 31-39, doi: 10.20965/jaciii.2021.p0031, 2021.
- [25] J.-H. Kim, “Further improvement of Jensen inequality and application to stability of time-delayed systems,” Automatica, Vol.64, pp. 121-125, 2016.
- [26] X. M. Zhang, Q. L. Han, and X. Ge, “Novel stability criteria for linear time-delay systems using Lyapunov-Krasovskii functionals with a cubic polynomial on time-varying delay,” IEEE CAA J. Autom. Sinica, Vol.8, No.1, pp. 77-85, 2021.
- [27] W. Kwon, B. Koo, and S. M. Lee, “Novel Lyapunov–Krasovskii functional with delay-dependent matrix for stability of time-varying delay systems,” Appl. Math. Comput., Vol.320, pp. 149-157, 2018.
 This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.
This article is published under a Creative Commons Attribution-NoDerivatives 4.0 Internationa License.