Taking on a new challenge: solving GeeksforGeeks POTD daily and sharing my solutions! 💻🔥
The goal: sharpen problem-solving skills, level up coding, and learn something new every day. Follow my journey! 🚀

100DaysOfCode #CodingChallenge #ProblemSolving #GeeksforGeeks #DeveloperJourney

Problem:

https://www.geeksforgeeks.org/problems/second-best-minimum-spanning-tree/1

Second Best Minimum Spanning Tree

Difficulty: Medium Accuracy: 52.73%

Given an undirected graph of V vertices numbered from (0 to V-1) and E edges represented by a 2D array edges[][], where each edges[i] contains three integers [u, v, w], representing an undirected edge from u to v, having weight w.
Your task is to find the weight of the second best minimum spanning tree of the given graph.
A second best MST is defined as the minimum-weight spanning tree whose total weight is strictly greater than the weight of the minimum spanning tree.
Note: If no such second best MST exists, return -1.
Examples:
Input: V = 5, E = 7, edges[][] = [[0, 1, 4], [0, 2, 3], [1, 2, 1], [1, 3, 5], [2, 4, 10], [2, 3, 7], [3, 4, 2]]

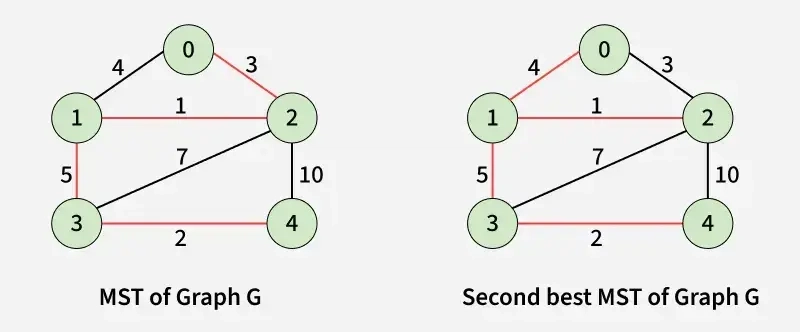
Output: 12
Explanation:

Input: V = 5, E = 4, edges[][] = [[0, 1, 2], [1, 2, 3], [2, 3, 4], [3, 4, 5]]

Output: -1
Explanation: No second best MST exists for this graph.

Constraints:
1 ≤ V ≤ 100
V-1 ≤ E ≤ V*(V-1)/2
0 ≤ edges[i][2] ≤ 103

Solution:
class Solution:
def secondMST(self, V, edges):
edges.sort(key=lambda x: x[2])
parent=list(range(V))
rank=[0]*V

    def find(x):
        while parent[x]!=x:
            parent[x]=parent[parent[x]]
            x=parent[x]
        return x

    def union(a,b):
        ra,rb=find(a),find(b)
        if ra==rb: return False
        if rank[ra]<rank[rb]: parent[ra]=rb
        elif rank[rb]<rank[ra]: parent[rb]=ra
        else: parent[rb]=ra; rank[ra]+=1
        return True

    mst=[]
    mst_weight=0
    for u,v,w in edges:
        if union(u,v):
            mst.append((u,v,w))
            mst_weight+=w

    if len(mst)!=V-1: return -1

    ans=float('inf')

    for rem in mst:
        parent=list(range(V))
        rank=[0]*V
        w2=0
        cnt=0
        for u,v,w in edges:
            if (u,v,w)==rem: continue
            if union(u,v):
                w2+=w
                cnt+=1
        if cnt==V-1 and w2>mst_weight:
            ans=min(ans,w2)

    return ans if ans!=float('inf') else -1