Some Properties of k-Jacobsthal Numbers with Arithmetic Indexes
Deepika Jhala1, , G.P.S. Rathore2, Kiran Sisodiya1
, G.P.S. Rathore2, Kiran Sisodiya1
1School of Studies in Mathematics, Vikram University, Ujjain (India)
2College of Horticulture, Mandsaur (M.P.)
Abstract
In this paper, we derive various formulae for the sum of k-Jacobsthal numbers with indexes in an arithmetic sequence, say an+r for fixed integers a and r Also, we describe generating function and the alternated sum formula for k-Jacobsthal numbers with indexes in an arithmetic sequence.
Keywords: k-jacobsthal numbers, binet formula, generating function
Turkish Journal of Analysis and Number Theory, 2014 2 (4),
pp 119-124.
DOI: 10.12691/tjant-2-4-3
Received June 08, 2014; Revised July 13, 2014; Accepted July 23, 2014
Copyright © 2013 Science and Education Publishing. All Rights Reserved.Cite this article:
- Jhala, Deepika, G.P.S. Rathore, and Kiran Sisodiya. "Some Properties of k-Jacobsthal Numbers with Arithmetic Indexes." Turkish Journal of Analysis and Number Theory 2.4 (2014): 119-124.
- Jhala, D. , Rathore, G. , & Sisodiya, K. (2014). Some Properties of k-Jacobsthal Numbers with Arithmetic Indexes. Turkish Journal of Analysis and Number Theory, 2(4), 119-124.
- Jhala, Deepika, G.P.S. Rathore, and Kiran Sisodiya. "Some Properties of k-Jacobsthal Numbers with Arithmetic Indexes." Turkish Journal of Analysis and Number Theory 2, no. 4 (2014): 119-124.
| Import into BibTeX | Import into EndNote | Import into RefMan | Import into RefWorks |
1. Introduction
The Fibonacci sequence and the Lucas sequence are the two shining stars in the vast array of integer sequences. They have fascinated both amateurs and professional mathematicians for centuries. Also they continue to charm us with their beauty, their abundant applications, their ubiquitous habit of occurring in totally surprising and unrelated places. Fibonacci numbers have been generalized by different authors. Some authors have generalized the Fibonacci sequence by preserving the recurrence relation and altering the first two terms of the sequence [A Generalized Fibonacci Sequence, The American Mathematical Monthly, 1961, 68, 455-459.">10, On a Generalized Fibonacci Sequence, Labdev Journal of Science and Technology, Part A, 1969, 7, 67-71.">12, Some Further Identities for the Generalized Fibonacci sequence, Fibonacci Quarterly, 1974, 12 (3), 272-280.">17], while others have generalized the Fibonacci sequence by preserving the first two terms but altering the recurrence relation slightly [The Binet Formula and the Representation of k-Generalized Fibonacci Numbers, Fibonacci Quarterly, 2001, 39 (2), 158-164.">14, On the k-Ggeneralized Fibonacci Matrix Qk, Linear Algebra Applications, 1997, 251, 73-88.">15, Some Properties of the Generalization of the Fibonacci Sequence, Fibonacci Quarterly, 1987, 25 (2), 111-117.">18].
More recently, Fibonacci, Lucas, Pell, Pell-Lucas, Modified Pell, Jacobhstal, Jacobsthal-Lucas sequences were generalized for any positive real number k. Also the study of the k-Fibonacci sequence, the k-Lucas sequence, the k-Pell sequence, the k-Pell-Lucas sequence, the Modified k-Pell sequence, the k-Jacobhstal sequence and the k-Jacobsthal Lucas sequence appeared (see [1-6,8,13]). Falcon and plaza [7] has given several formulae for the sum of k-Fibonacci numbers with indexes in an arithmetic sequence. Falcon [9] defines the k-Lucas number with indexes in an arithmetic sequence. Also, deduced generating function and several sum formulae for these numbers with indexes in an arithmetic sequence.
1.1. k - Jacobsthal and k - Jacobsthal Lucas Numbers1.1.1. Definition 1.1 (k-Jacobsthal Numbers)
For any positive real number k, the k-Jacobsthal sequence say [13] is defined recurrently by
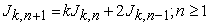 | (1.1) |
with initial conditions .
.
Particular cases of definition (1.1)
If 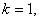 we obtain the Jacobsthal sequence [11]
we obtain the Jacobsthal sequence [11] 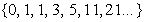 (A001045) [16]
(A001045) [16]
If 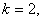 we obtain the sequence
we obtain the sequence 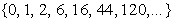 A002605 [16].
A002605 [16].
First few terms of the k-Jacobsthal numbers (1.1) are
 |
 |
Some of the interesting properties that the k-Jacobsthal sequence satisfies are summarized as below [13]:
1.1.1.1. Binet’s Formula
The Binet formula for the nth k-Jacobsthal numbers is
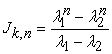 | (1.2) |
where  ,
, 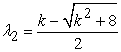 are the roots of the characteristic equation
are the roots of the characteristic equation 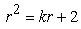 associated to the recurrence relation defined in equation (1.1) and
associated to the recurrence relation defined in equation (1.1) and 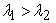 ,
,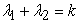 ,
, 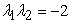 ,
,  .
.
1.1.1.2. Catalan’s Identity
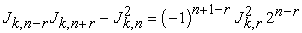 | (1.3) |
1.1.1.3. D’Ocagne Identity
If m > n then
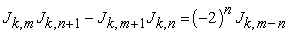 | (1.4) |
1.1.1.4. Convolution Product
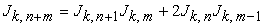 | (1.5) |
Now, we introduce the k-Jacobsthal Lucas sequence, whose recurrence relation is the same as the k-Jacobsthal sequence.
1.2. Definition 1.2For any positive real number k, the k-Jacobsthal-Lucas sequence say [2] is defined recurrently by
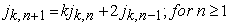 | (1.6) |
with initial conditions 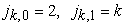 .
.
As particular cases:
If  we obtain the Jacobsthal-Lucas sequence [11]
we obtain the Jacobsthal-Lucas sequence [11] 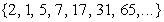 (A014551) [16].
(A014551) [16].
If  we obtain the sequence
we obtain the sequence 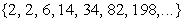 A080040 [16].
A080040 [16].
First few terms of the k-Jacobsthal Lucas numbers equation (1.6) are
 |
Some of the interesting properties that the k-Jacobsthal Lucas sequence satisfies are summarized as below [2].
1.2.1. Binet’s Formula
The Binet formula for the k-Jacobsthal numbers is
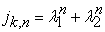 | (1.7) |
where 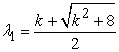 ,
, 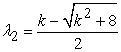 are the roots of the characteristic equation
are the roots of the characteristic equation 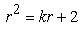 ,
, 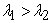
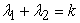 ,
, 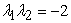 and
and 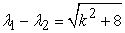 associated to the recurrence relation defined in equation (1.6).
associated to the recurrence relation defined in equation (1.6).
1.2.2. Catalan’s Identity
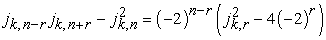 | (1.8) |
1.2.3. D’Ocagne Identity
If m > n then
 | (1.9) |
Now, we prove some properties of the k-Jacobsthal numbers that we will be needed later.
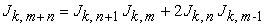 | (1.10) |
Proof: Taking R.H.S. and applying the Binet’s formula for k-Jacobsthal numbers
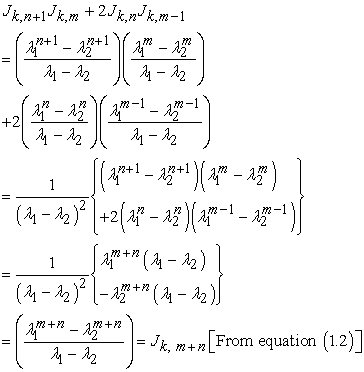 |
That is 
 | (1.11) |
Proof: We will prove this by using the Mathematical induction method. For
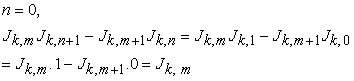 |
we see that it is true for 
Now for 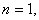 we have
we have
 |
again we see that it is true for 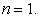
Now, suppose the formula is true until 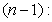
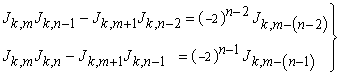 | (1.12) |
Then,
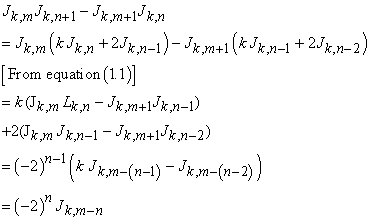 |
That is 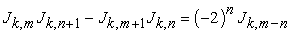 .
.
2. On the k-Jacobsthal Numbers of Kind an+r
In this section, we shall derive some formulae for the sums of the k- Jacobsthal numbers with index in an arithmetic sequence, say 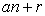 for fixed integer a and r such that
for fixed integer a and r such that 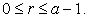 Also, we have discuss generating function for these numbers with index in an arithmetic sequence.
Also, we have discuss generating function for these numbers with index in an arithmetic sequence.
First we prove following lemmas that will be needed later.
2.1. Lemma 2.1For all integers 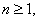
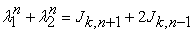 | (2.1) |
Proof: Taking R.H.S. and applying the Binet’s formula for k-Jacobsthal numbers and 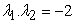 .
.
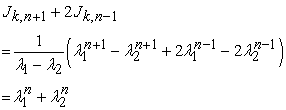 |
That is 
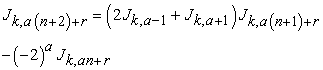 | (2.2) |
Proof: Taking R.H.S. and applying Binet’s formula and Lemma 2.1.
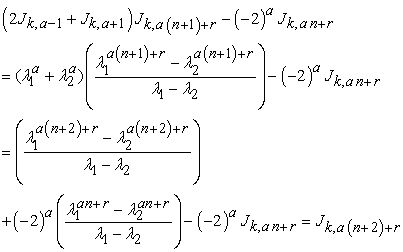 |
now, since 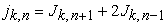 , then the above formula can be rewritten as
, then the above formula can be rewritten as
 |
equation (2.2) gives the general term of the k-Jacobsthal sequence 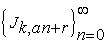 as a linear combination of the two preceding terms.
as a linear combination of the two preceding terms.
2.2.1. Generating Function for the Sequence
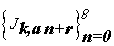
Suppose that 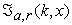 be the generating function of the sequence
be the generating function of the sequence 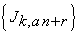 with
with 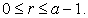 That is
That is
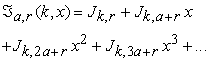 | (2.3) |
Now multiplying both sides by the algebraic expression 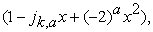 we get
we get
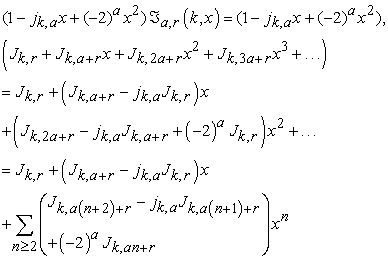 |
Now, from equation (2.2), the summation of right hand side of the above equation vanishes. That is
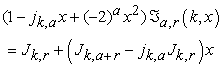 | (2.4) |
from equation (1.10), we have
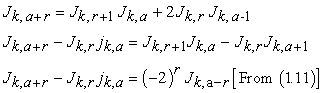 |
Hence equation (2.4) becomes
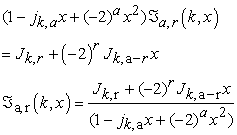 | (2.5) |
Particular cases:
For the different values of a and r, the generating function of the sequences  are:
are:
1) If 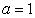 and then
and then ,
,
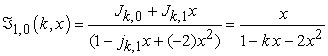 |
which is the generating function of the k-Jacobsthal sequence [13].
2) If 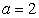 , then
, then
At 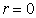 ,
,
 |
At 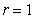 ,
,
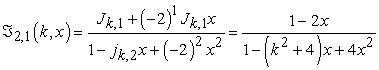 |
3) If 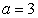 , then
, then
At  ,
,
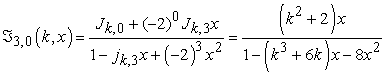 |
At  ,
,
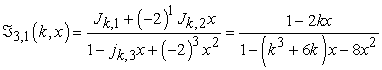 |
At 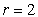 ,
,
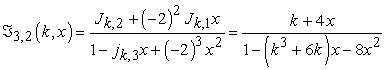 |
2.2.2. Sum of k-Jacobsthal numbers with arithmetic index
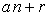
In this section, we have discuss the sum formula for the k-Jacobsthal numbers with arithmetic index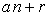 , where a and r are fixed integer such that
, where a and r are fixed integer such that 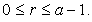
Sum of k-Jacobsthal number of kind 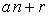 is
is
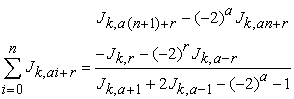 | (2.6) |
Proof: Applying Binet’s formula for the k- Jacobsthal numbers, we have
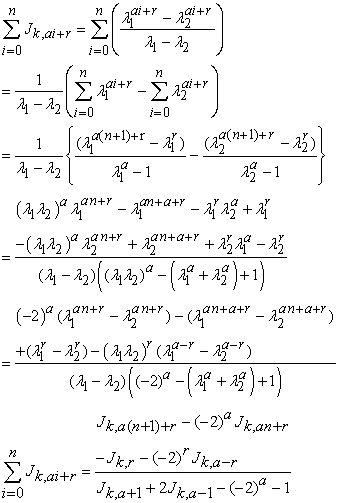 |
Formula for sum of odd k-Jacobsthal numbers
If 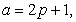 then equation (2.6) gives
then equation (2.6) gives
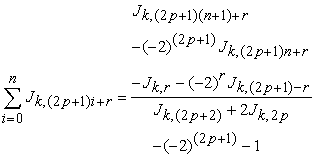 | (2.7) |
For example: (1) If 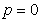 , then
, then 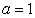 and
and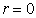 , we have
, we have
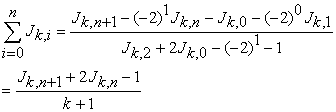 |
(2) If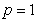 , then
, then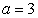 , we have
, we have
 |
If 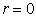 , then
, then
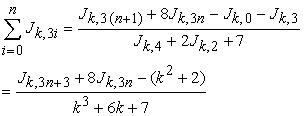 |
If 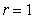 , then
, then
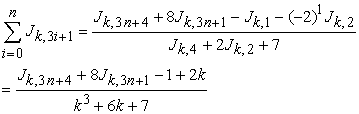 |
If 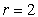 , then
, then
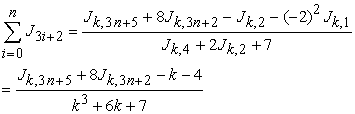 |
(3) If 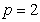 , then
, then 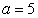 , we have
, we have
 |
If 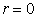 , then
, then
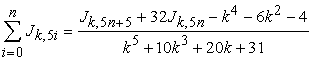 |
If 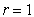 , then
, then
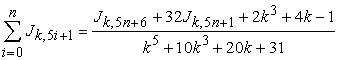 |
If 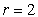 , then
, then
 |
If 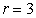 , then
, then
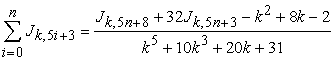 |
If 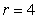 , then
, then
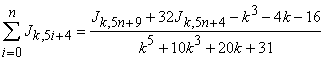 |
Sum of even k-Jacobsthal numbers.
If 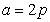 , then equation (2.6) is
, then equation (2.6) is
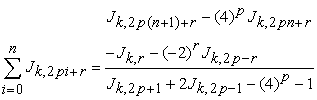 | (2.8) |
For example: (1) If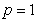 , then
, then  , we have
, we have
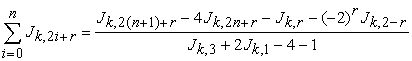 |
If 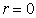 , then
, then
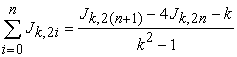 |
If 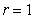 , then
, then 
(2) If 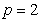 , then
, then 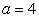 , we have
, we have
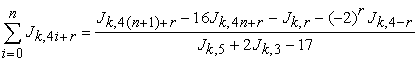 |
If 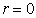 , then
, then
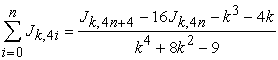 |
If 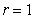 , then
, then
 |
If 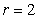 , then
, then
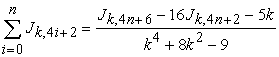 |
If 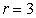 , then
, then
 |
Now, we have considered the alternating sequence  . By the previous method we can also find the sum formula for this sequence.
. By the previous method we can also find the sum formula for this sequence.
Alternating sum of the k-Jacobsthal numbers with index 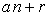 is given by
is given by
 | (2.9) |
Proof: Taking L.H.S. and applying the binet formula for the k-Jacobsthal numbers equation (1.2) we have
 |
that is
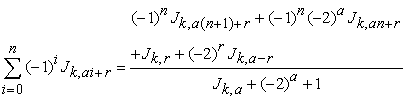 |
For different values of a and r, the above sum can be written as
For  we have
we have 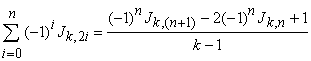
For, 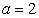
 |
a) If 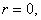 then
then
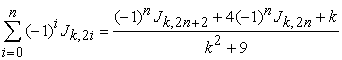 |
b) If 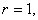 then
then
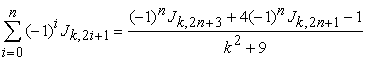 |
For 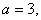
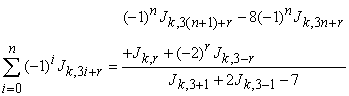 |
If  then
then
 |
If 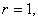 then
then
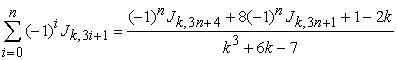 |
If 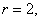 then
then
 |
Reference
| [1] | Bolat C., Kose H., On the Properties of k-Fibonacci Numbers. Int. J.Contemp. Math. Sciences 2010, 22 (5), 1097-1105. | ||
 In article In article | |||
| [2] | Campos H., Catarino P., Aires A.P., Vasco P. and Borges A., On Some Identities of k-Jacobsthal-Lucas Numbers, Int. Journal of Math. Analysis, 2014, 8 (10), 489-494. | ||
 In article In article | |||
| [3] | Catarino P., On Some Identities and Generating Functions for k-Pell Numbers. Int. Journal of Math. Analysis 2013, 7 (38), 1877-1884. | ||
 In article In article | |||
| [4] | Catarino P., Vasco P., Modified k-Pell Sequence: Some Identities and Ordinary Generating Function. Applied Mathematical Sciences 2013, 7 (121), 6031-6037. | ||
 In article In article | |||
| [5] | Catarino P., Vasco P., On some Identities and Generating Functions for k-Pell-Lucas Sequence. Applied Mathematical Sciences 2013, 7 (98), 4867-4873. | ||
 In article In article | |||
| [6] | Catarino P., On Some Identities for k-Fibonacci Sequence. International Journal of Contemporary mathematical Sciences 2014, 9 (1), 37-42. | ||
 In article In article | |||
| [7] | Falcon S. and Plaza A., On k-Fibonacci Numbers of Arithmetic Indexes, Applied Mathematics and Computation, 2009, 208, 180-185. | ||
 In article In article | CrossRef | ||
| [8] | Falcon S., On the k-Lucas Numbers, International Journal of Contemporary mathematical Sciences 2011, 6 (21), 1039-1050. | ||
 In article In article | |||
| [9] | Falcon S., On the k-Lucas Numbers of Arithmetic Indexes, Applied Mathematics, 2012, 3, 1202-1206. | ||
 In article In article | CrossRef | ||
| [10] | Horadam A. F., A Generalized Fibonacci Sequence, The American Mathematical Monthly, 1961, 68, 455-459. | ||
 In article In article | CrossRef | ||
| [11] | Horadam A.F., Jacobsthal Representation Numbers. Fibonacci Quarterly, 1996, 34 (1), 40-54. | ||
 In article In article | |||
| [12] | Jaiswal D. V., On a Generalized Fibonacci Sequence, Labdev Journal of Science and Technology, Part A, 1969, 7, 67-71. | ||
 In article In article | |||
| [13] | Jhala D., Sisodiya K., Rathore G.P.S., On Some Identities for k-Jacobsthal Numbers. Int. Journal of Math. Analysis 2013, 7 (2), 551-556. | ||
 In article In article | |||
| [14] | Lee G. Y., Lee S. G., Kim J. S., Shin H. K., The Binet Formula and the Representation of k-Generalized Fibonacci Numbers, Fibonacci Quarterly, 2001, 39 (2), 158-164. | ||
 In article In article | |||
| [15] | Lee G. Y., Lee S. G., Shin H. K., On the k-Ggeneralized Fibonacci Matrix Qk, Linear Algebra Applications, 1997, 251, 73-88. | ||
 In article In article | CrossRef | ||
| [16] | Slone NJA, The On-Line Encyclopedia of Integer Sequences, (2006), www.research.att.com/~njas/sequences/. | ||
 In article In article | |||
| [17] | Walton J. E. and Horadam A. F., Some Further Identities for the Generalized Fibonacci sequence, Fibonacci Quarterly, 1974, 12 (3), 272-280. | ||
 In article In article | |||
| [18] | Zai L. J. and Sheng L. J., Some Properties of the Generalization of the Fibonacci Sequence, Fibonacci Quarterly, 1987, 25 (2), 111-117. | ||
 In article In article | |||
- k-Jacobsthal Numbers with Arithmetic Indexes"
target="_blank" title="Add to CiteULike">
 CiteULike
CiteULike -
 Mendeley
Mendeley -
 StumbleUpon
StumbleUpon - k-Jacobsthal Numbers with Arithmetic Indexes"
title="Add to Delicious" target="_blank">
 Delicious
Delicious - k-Jacobsthal Numbers with Arithmetic Indexes"
title="Share on Facebook" target="_blank">
 Facebook
Facebook - k-Jacobsthal Numbers with Arithmetic Indexes https://pubs.sciepub.com/tjant/2/4/3/index.html"
onclick="truncateTweetText();" target="_blank" title="Share on Twitter" id="twitter-share-link">
 Twitter
Twitter - k-Jacobsthal Numbers with Arithmetic Indexes"
target="_blank" title="Add to LinkedIn">
 LinkedIn
LinkedIn
 OPEN ACCESS
OPEN ACCESS  PEER-REVIEWED
PEER-REVIEWED
