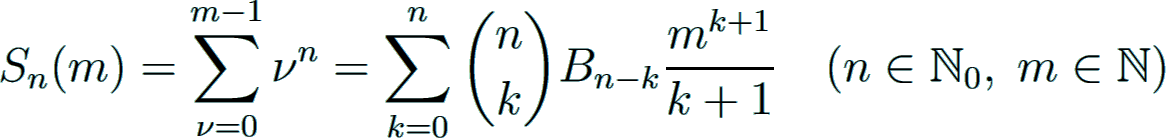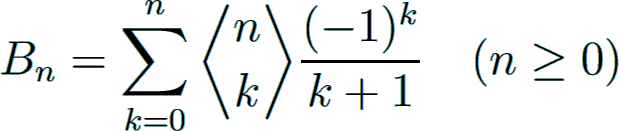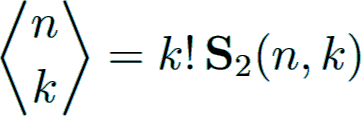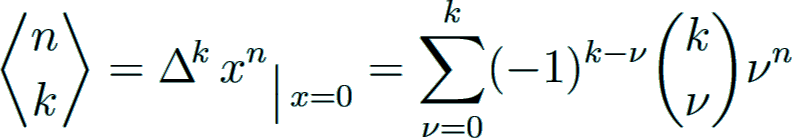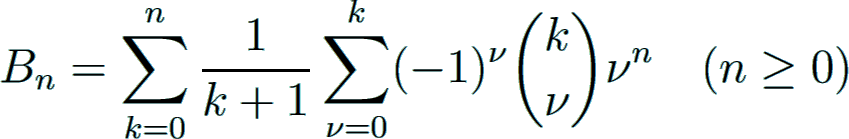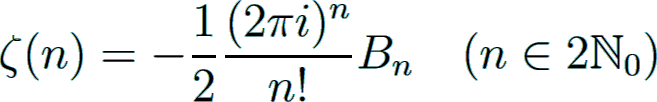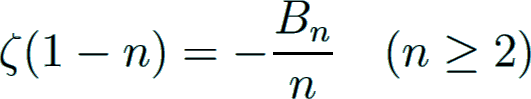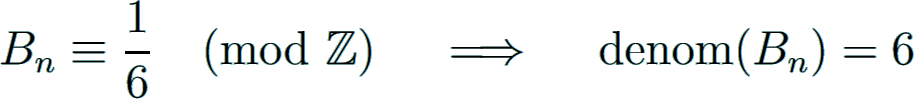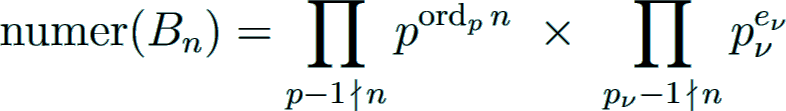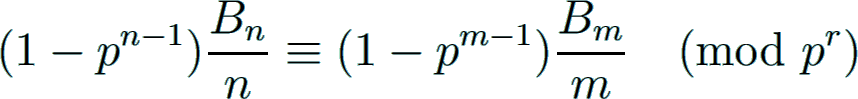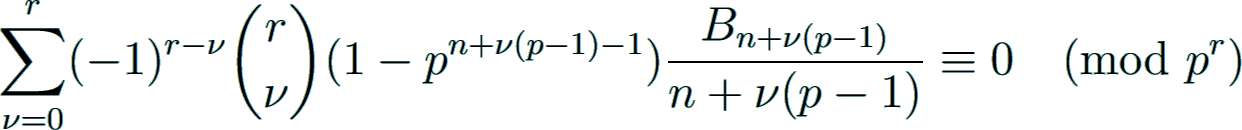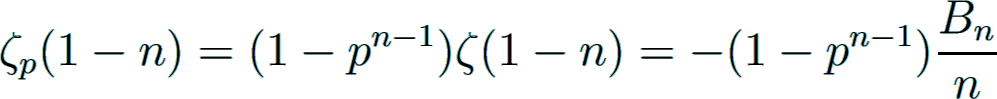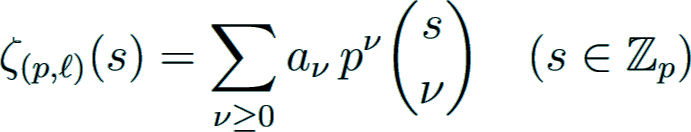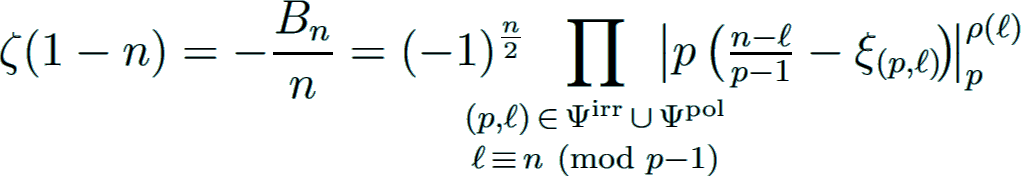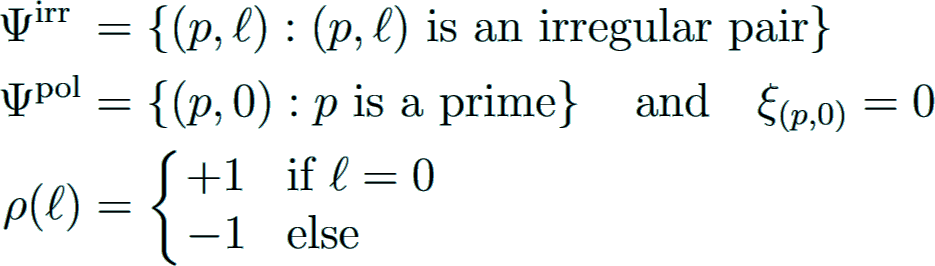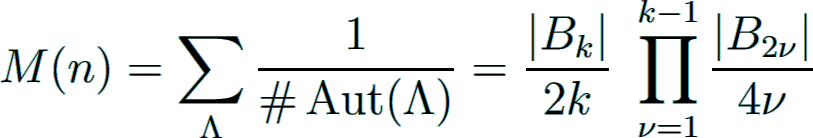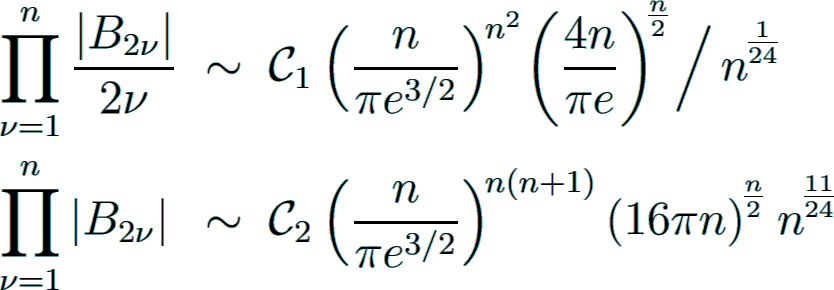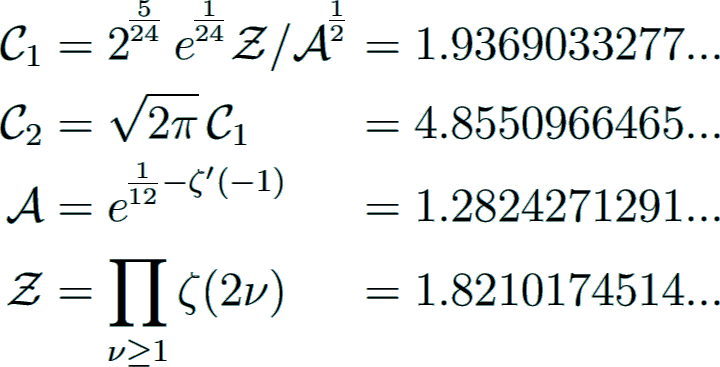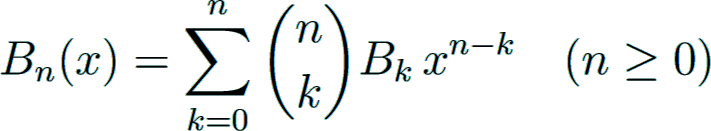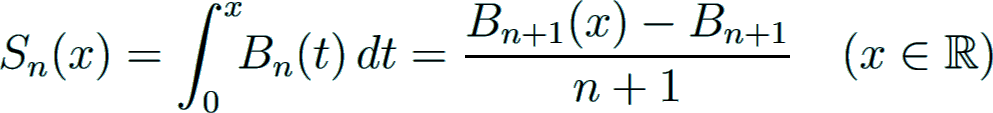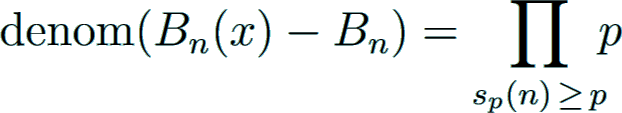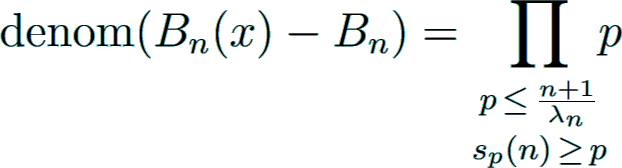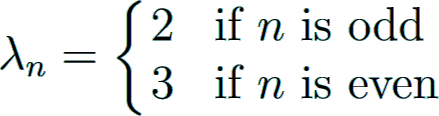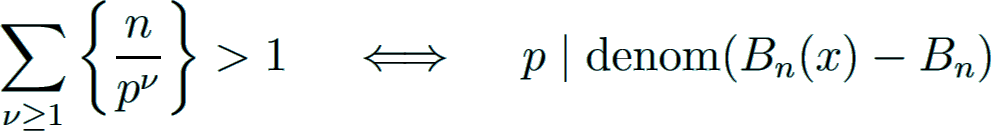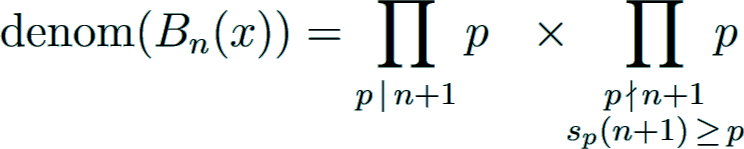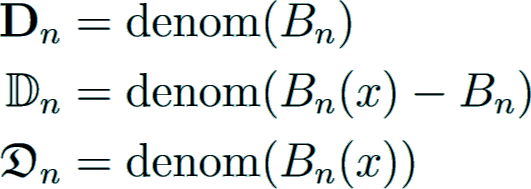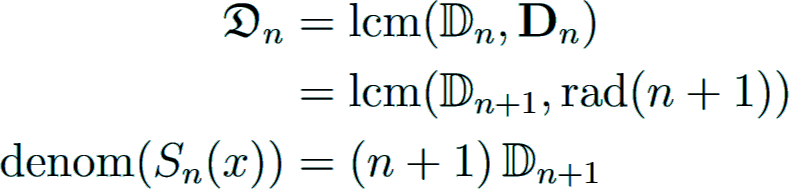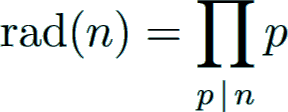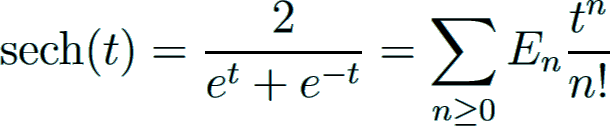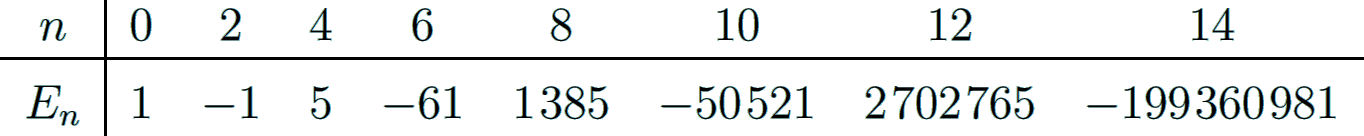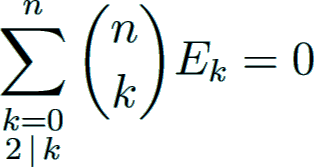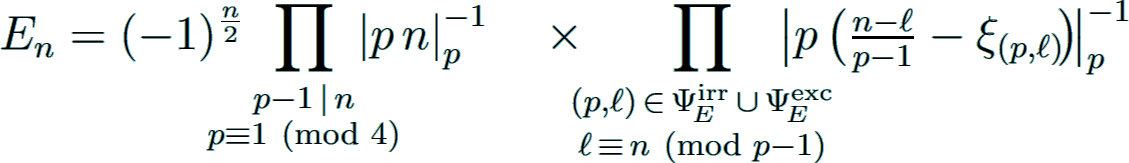Bernoulli numbers
Introduction
The Bernoulli numbers Bn play an important role in several topics of mathematics. These numbers can be defined by the power series
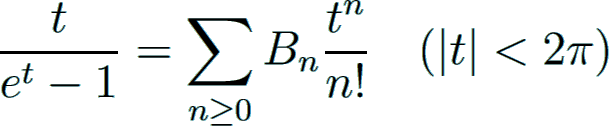
where all numbers Bn are zero with odd index n > 1. The even-indexed rational numbers Bn alternate in sign. First values are

The values can be computed iteratively by the recurrence formula

which can be written symbolically as
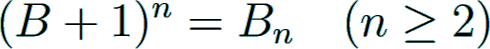
The sequences of the numerators and denominators of Bn are A027641 and A027642, respectively.
Sum of consecutive integer powers
Jacob Bernoulli Bernoulli1713 (1655-1705) introduced a sequence of rational numbers in his Ars Conjectandi, which was published posthumously in 1713.
He used these numbers, later called Bernoulli numbers, to compute the sum of consecutive integer powers.
This formula is given by
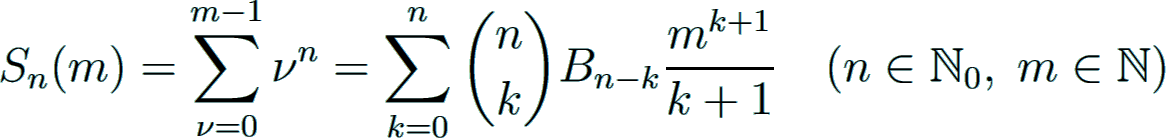
where Sn(x) is a polynomial of degree n + 1.
Explicit formulas
An explicit formula for Bn was derived by Worpitzky Worpitzky1883 in 1883:
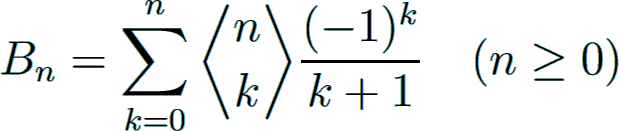
using the symbol
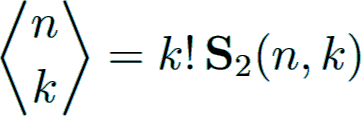
with S2(n, k) being the Stirling numbers of the second kind.
He also gave another formula for Sn(x):

Furthermore, one has by means of iterated forward differences the relation
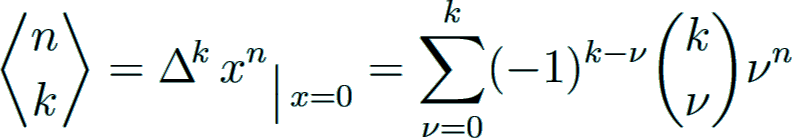
yielding the double sum
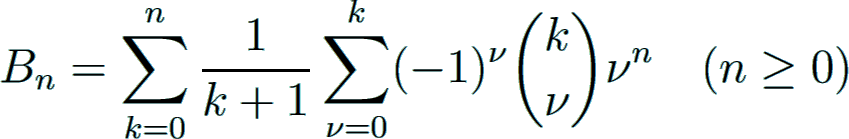
Special values of the Riemann zeta function
The Bernoulli numbers are connected with the Riemann zeta function

on the positive real axis by Euler's celebrated formula for positive even n, also valid for n = 0:
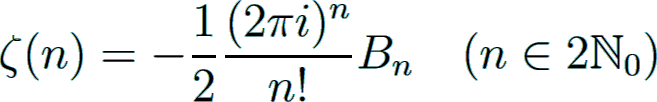
The functional equation of ζ(s) leads to the following formula for negative integer arguments:
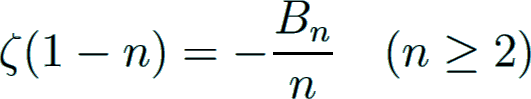
Regular and irregular primes
In 1850 Kummer Kummer1850 introduced two classes of odd primes, later called regular and irregular (see, e.g., Hilbert Hilbert1897;Chap.~31).
An odd prime p is called regular if p does not divide the class number of the cyclotomic field
 where
where 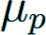 is the set of p-th roots of unity; otherwise irregular.
Kummer then proved that Fermat's Last Theorem is true, that is
is the set of p-th roots of unity; otherwise irregular.
Kummer then proved that Fermat's Last Theorem is true, that is
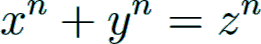
has no solution in positive integers x, y, and z, for the case when the exponent n is a regular prime.
He also provided an equivalent definition concerning Bernoulli numbers:
If p does not divide any of the numerators of the Bernoulli numbers B2, B4, …, Bp−3, then p is regular.
The irregular primes below 100 are 37, 59, and 67; see A000928.
In 1915 Jensen Jensen1915 proved that infinitely many irregular primes p exist with the restriction p ≡ 3 (mod 4).
Carlitz Carlitz1954 later gave a short (and weaker) proof without any restriction on p.
Unfortunately, it is still an open question whether infinitely many regular primes exist. However, several computations (see, e.g., Hart, Harvey, and Ong HartHarveyOng2017) suggest that about 60% of all primes are regular, which agree with an expected distribution proposed by Siegel Siegel1964.
Irregular pairs
The pair (p, ℓ) is called an irregular pair, if p divides the numerator of Bℓ where ℓ is even and 2 ≤ ℓ ≤ p − 3.
The index of irregularity i(p) is defined to be the number of such pairs belonging to p. If i(p) = 0, then p is regular, otherwise irregular.
The first irregular pairs are (37, 32), (59, 44), and (67, 58).
The irregular prime p = 157 is the least prime with i(p) = 2: (157, 62), (157, 110).
Structure of the denominator
The denominator of Bn for positive even n
is given by the famous von Staudt-Clausen theorem, independently found by von Staudt Staudt1840 and Clausen Clausen1840 in 1840:

As a consequence, the denominator is squarefree and divisible by 6.
Given a Bernoulli number Bn with n even, Rado Rado1934 showed that there exist infinitely many even m such that
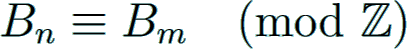
implying that the numbers Bm have the same denominator as Bn.
A special case is given for n = 2p, where p is an odd prime p ≡ 1 (mod 3):
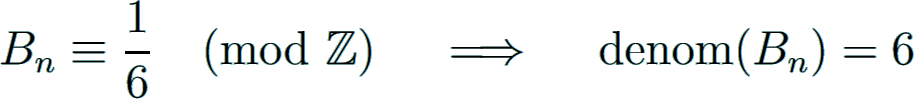
See A112772, which is a subsequence of A051222; the sequence of the increasing denominators is A090801.
Structure of the numerator
The unsigned numerator of the divided Bernoulli number Bn/n for positive even n equals 1 only for n = 2, 4, 6, 8, 10, 14;
otherwise the numerator consists of a product of powers of irregular primes:

Since Bn/n is a p-integer for all primes p with p − 1 not dividing n, the structure of the numerator of Bn is given by
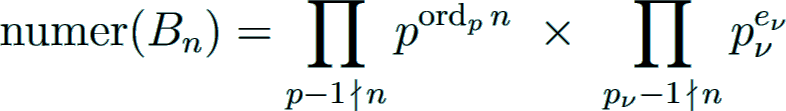
The additional left product is a trivial factor of Bn that divides n, see A300711.
For the signed numerators of Bn and Bn/n for even n see A000367 and A001067, respectively.
Kummer congruences
The Kummer congruences describe the most important arithmetical properties of the Bernoulli numbers, which give a modular relation between these numbers.
Let φ denote Euler's totient function. Let n and m be positive even integers and p be a prime with p − 1 ∤ n.
If n ≡ m (mod φ(pr)) where r ≥ 1, then
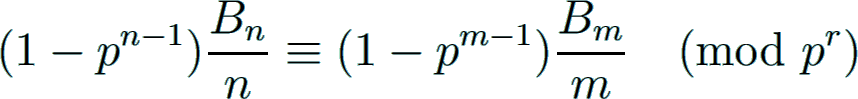
Furthermore,
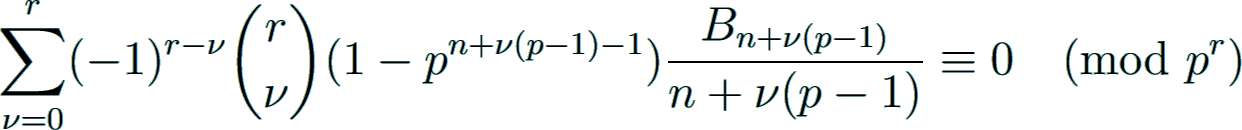
In 1851 Kummer Kummer1851 originally introduced these congruences without the Euler factors (1 − pn−1) and hence with restrictions on r and n.
He showed that the second congruence holds for n > r, whereas the first congruence was derived from the latter only for r = 1
(in these cases the Euler factors vanish). Subsequently, these congruences were widely generalized by several authors (see, e.g., Fresnel Fresnel1967).
Constructing p-adic zeta functions
The values ζ(1 − n) = −Bn/n and the Kummer congruences lead to the construction of p-adic zeta and L-functions, as introduced by Kubota and Leopoldt KubotaLeopoldt1964 in 1964.
One kind of their constructions deals with p-adic zeta functions defined in certain residue classes; for a detailed theory see Koblitz Koblitz1996;Chap. II.
For a prime p and even n ≥ 2 define the zeta function
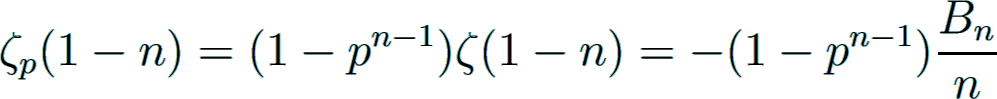
Let p ≥ 5 and ℓ ∈ {2, 4, …, p − 3} be fixed.
Define the p-adic zeta function on  by
by

for p-adic integers s by taking any sequence (tν)ν ≥ 1 of nonnegative integers that p-adically converges to s.
Indeed, this function is well-defined and has the following properties.
At nonnegative integer arguments the function ζ(p,ℓ)(s) interpolates values of the function ζp(1 − n).
The Kummer congruences then state for r ≥ 1 that
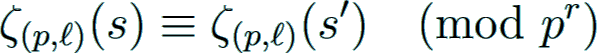
when s ≡ s' (mod pr−1) for nonnegative integers s and s'.
Since ℤ is dense in ℤp, the function ζ(p,ℓ)(s), restricted on nonnegative integer arguments, uniquely extends, by means of the Kummer congruences and preserving the interpolation property, to a continuous function on ℤp.
Zeros of p-adic zeta functions
The p-adic zeta function ζ(p,ℓ)(s) can be written as a special Mahler expansion (Kellner Kellner2007):
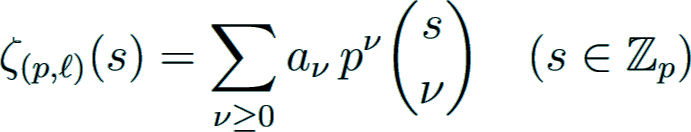
with integral coefficients
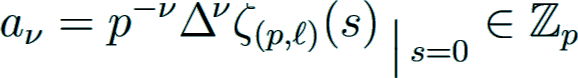
One has the relation

Condition for the existence of a unique simple zero (Kellner Kellner2007):
If (p, ℓ) is an irregular pair and a1 ∈ 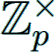 , that is
, that is

then the p-adic zeta function ζ(p,ℓ)(s) has a unique simple zero ξ(p,ℓ) ∈  .
.
So far, no irregular pair (p, ℓ) has been found that the non congruence relation above holds as a congruence.
Example: In the case (p, ℓ) = (37, 32) one computes that

For more p-adic digits see Kellner Kellner2007 and A299468.
Irregular pairs of higher order
The irregular pairs of higher order describe the first appearance of higher powers of irregular prime factors of Bn/n.
An irregular pair (p, n) of order r has the property that
pr divides Bn/n with n < φ(pr) = (p − 1)pr−1.
For r = 1 this gives the usual definition of irregular pairs, since the condition p divides Bn/n is then equal to p divides Bn.
A zero of the p-adic zeta function ζ(p,ℓ)(s) describes the irregular pairs (p, n) of higher order with n ≡ ℓ (mod p − 1),
and vice versa (Kellner Kellner2007).
For example, one obtains for the irregular pair (37, 32) that

and
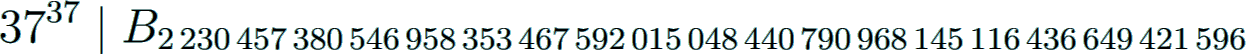
Irregular pairs of higher order can be effectively and easily computed using Bernoulli numbers with small indices. By this means one can even predict the extremely huge index of the first occurrence of the power 3737 as listed above; see A251782.
Conjecture on the structure of the Bernoulli numbers
Under the assumption that every p-adic zeta function ζ(p,ℓ)(s) has a unique simple zero ξ(p,ℓ)
in case (p, ℓ) is an irregular pair, one has for even n ≥ 2 (Kellner Kellner2007):
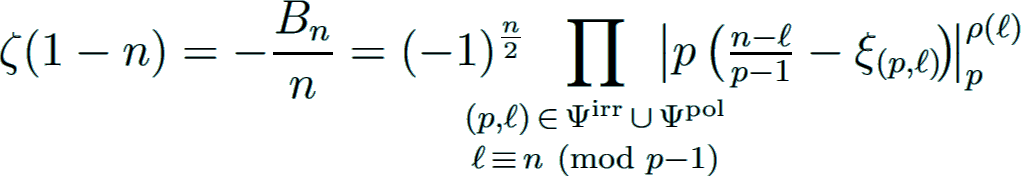
where
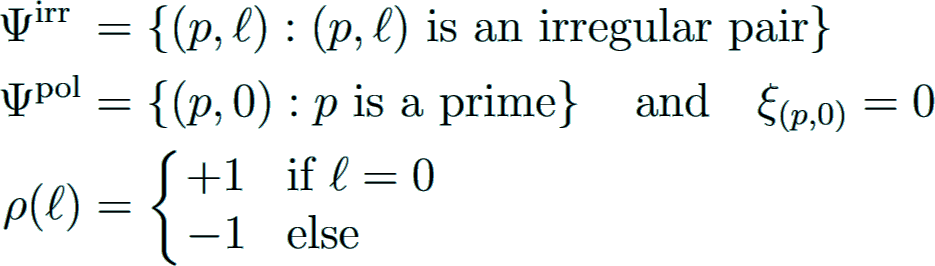
and |·|p is the ultrametric p-adic absolute value.
The denominator can be described by poles (always lying at ξ(p,0) = 0) and the numerator by zeros of p-adic zeta functions. Equivalently, the formula reads for the Bernoulli numbers:

The first product gives the trivial factor, the second product describes the product over irregular prime powers, and the third product yields the denominator of Bn.
Moreover, the formulas are valid for all irregular pairs (p, ℓ) with

This follows by computations of irregular pairs and cyclotomic invariants in that range by Hart, Harvey, and Ong HartHarveyOng2017. So far, no counterexample is known.
Class numbers of imaginary quadratic fields
Let h(d) denote the class number of the imaginary quadratic field
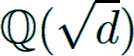 of discriminant d < −4.
There is the following connection with the Bernoulli numbers due to Carlitz Carlitz1953.
of discriminant d < −4.
There is the following connection with the Bernoulli numbers due to Carlitz Carlitz1953.
If p > 3 is a prime with p ≡ 3 (mod 4), then
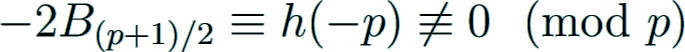
using the well-known relation that h(−p) < p. This implies that p cannot divide the above Bernoulli number.
Therefore, an irregular pair (p, (p + 1)/2) cannot exist when p ≡ 3 (mod 4).
Asymptotic formulas
The Minkowski-Siegel mass formula states for positive integers n = 2k with 8 ∣ n that
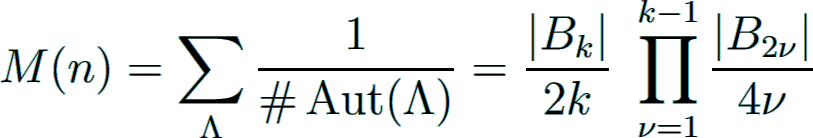
where the sum runs over all even unimodular lattices Λ in dimension n and Aut(Λ) is the automorphism group of Λ.
The products of (divided) Bernoulli numbers with explicit asymptotic constants (Kellner Kellner2009) are given by
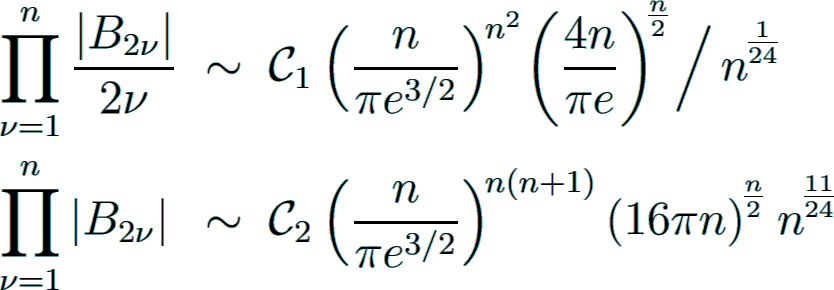
with
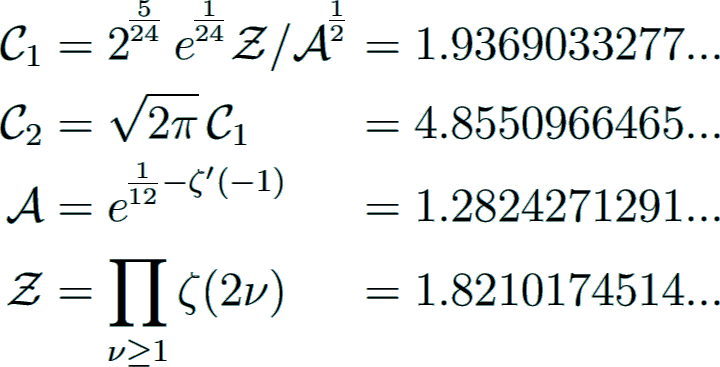
where  is the Glaisher-Kinkelin constant A074962
and
is the Glaisher-Kinkelin constant A074962
and 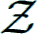 is the product over all Riemann zeta values at even positive integer arguments A080729.
is the product over all Riemann zeta values at even positive integer arguments A080729.
Euler numbers
Introduction
The Euler numbers En may be defined by the power series of the hyperbolic secant function
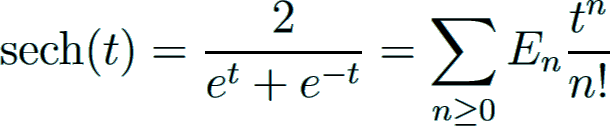
which is an even function implying that all En = 0 with odd index n.
The even-indexed numbers En are integers and alternate in sign. The first values (A028296) are
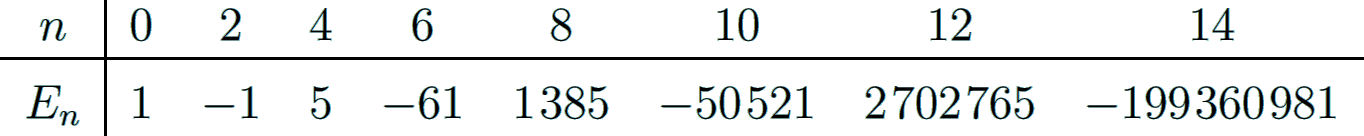
The values can be computed iteratively for even n ≥ 2 by the recurrence formula
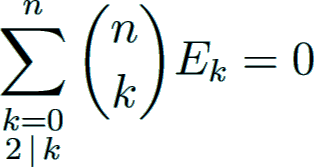
which can be written symbolically as
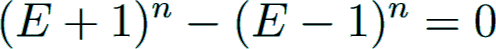
E-irregular primes and pairs
A prime p is called E-irregular, if p divides at least one of the Euler numbers E2, E4, …, Ep−3;
otherwise p is E-regular.
The pair (p, ℓ) is called an E-irregular pair, if p divides Eℓ where ℓ is even and 2 ≤ ℓ ≤ p − 3.
The index of E-irregularity iE(p) is defined to be the number of such pairs belonging to p.
The first E-irregular pairs are (19, 10), (31, 22), and (43, 12); see A120337.
The E-irregular prime p = 241 is the least prime with iE(p) = 2: (241, 210), (241, 238).
In 1954 Carlitz Carlitz1954 proved that infinitely many E-irregular primes exist. Later Ernvall Ernvall1975 showed the more specialized result that infinitely many E-irregular primes p ≢ ±1 (mod 8) exist.
As in the case of the Bernoulli numbers, it is still an open question whether infinitely many E-regular primes exist.
Conjecture on the structure of the Euler numbers
For the Euler numbers one can state a similar conjectural formula as in the case of the Bernoulli numbers, though it is a bit more complicated.
One may conjecturally state for even n ≥ 2 that
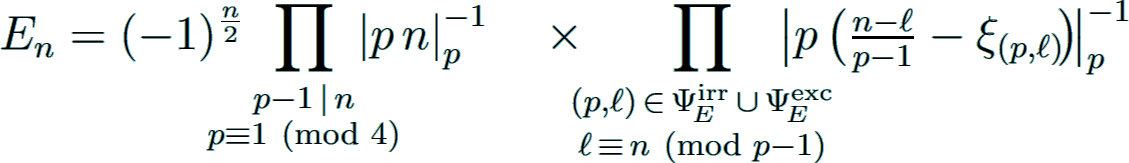
where ξ(p,ℓ) is the unique simple zero of a certain p-adic L-function
associated with an E-irregular pair (p, ℓ) ∈  when ℓ ≠ 0,
respectively, with a rare exceptional prime p with (p, 0) ∈
when ℓ ≠ 0,
respectively, with a rare exceptional prime p with (p, 0) ∈  in case ℓ = 0.
in case ℓ = 0.
Class numbers of imaginary quadratic fields
Let h(d) denote the class number of the imaginary quadratic field 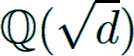 of discriminant d < −4.
Due to Carlitz Carlitz1953 one has the following connection with the Euler numbers.
of discriminant d < −4.
Due to Carlitz Carlitz1953 one has the following connection with the Euler numbers.
If p is a prime with p ≡ 1 (mod 4), then
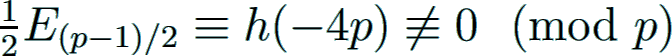
using the well-known relation h(−4p) < p. Therefore p cannot divide the above Euler number. Consequently, an E-irregular pair (p, (p − 1)/2) cannot exist when p ≡ 1 (mod 4).
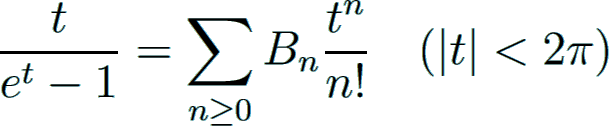


![]()